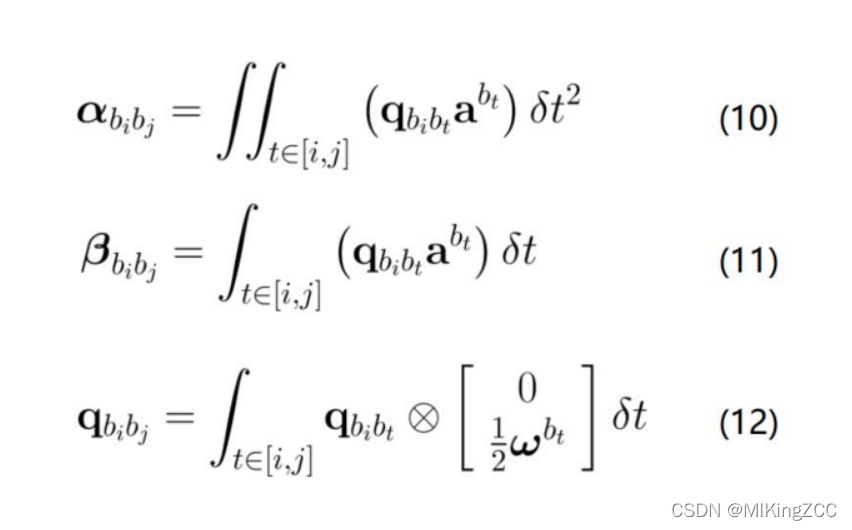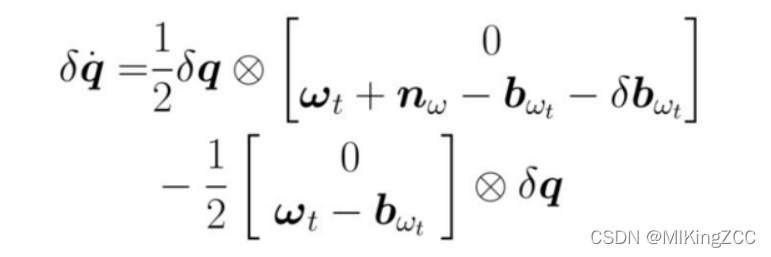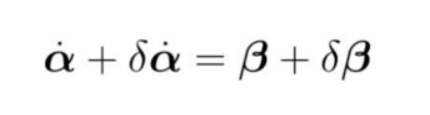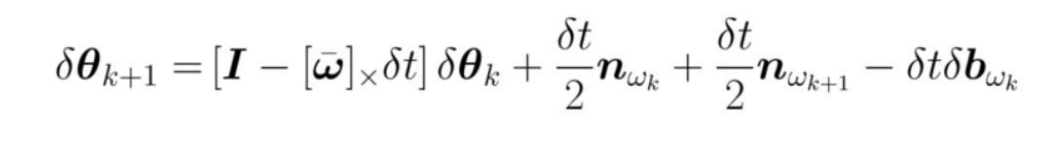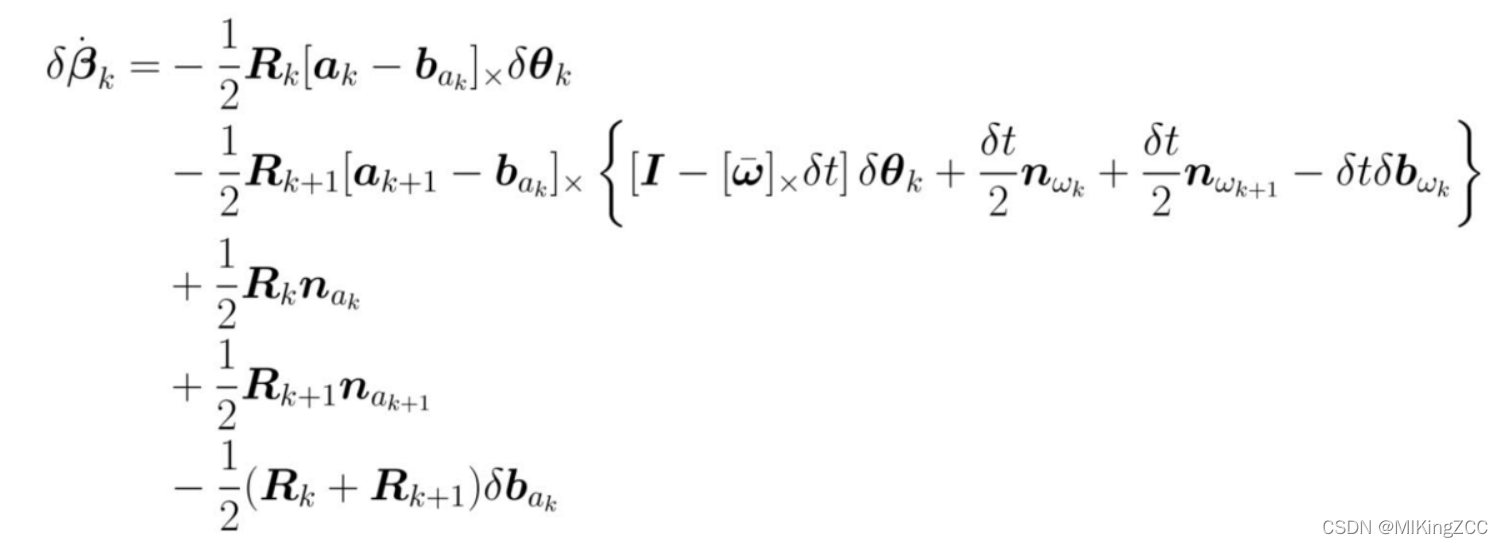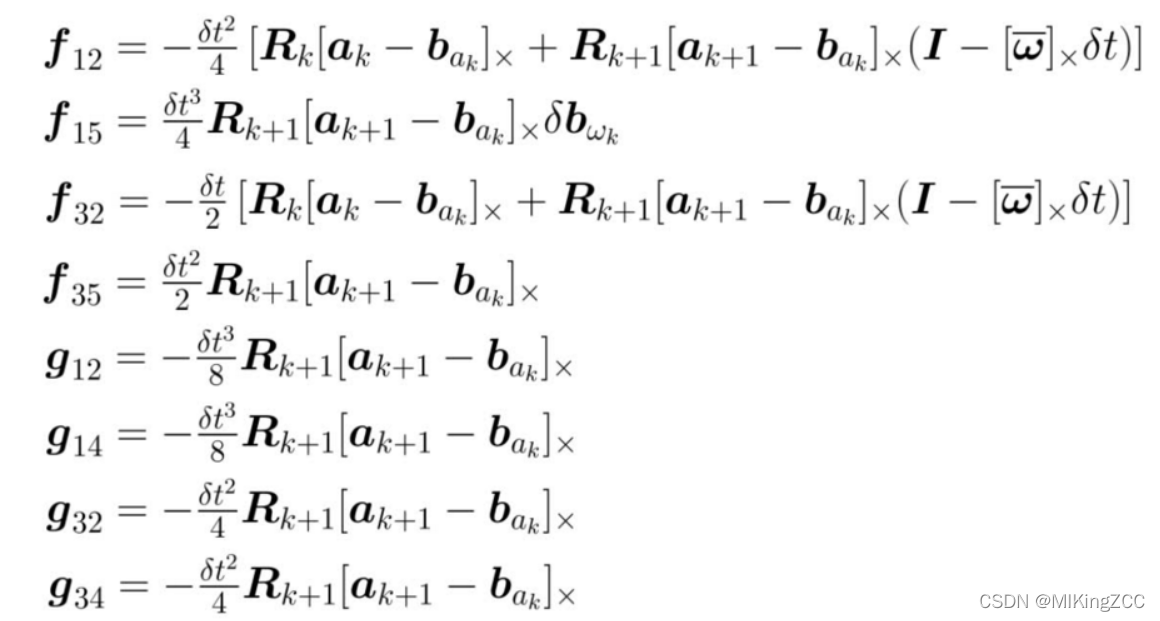当我们考虑一个SLAM的优化问题时，每进行一次迭代优化其对应的位姿就会改变一次，由于IMU的惯性积分需要依赖于一个位姿的初值，所以导致每次迭代优化后IMU就要重新计算一次，这会导致代码运算量过大，所以我们引入了预积分的概念，即直接计算两帧之间的相对位姿，而不依赖初值。

1.预积分计算

对于预积分的计算，我们首先要弄清楚IMU的惯性积分过程。首先，我们可以不加推导的得到一个运动微分方程:

根据上述微分方程，我们可以计算出从$i$时刻到$j$时刻IMU积分的结果：

根据预积分的要求，需要求的是相对结果，而且不依赖于上一时刻位姿，因此需要对上式做转换。
由于$q_{w{b}_t}=q{q}_{w{b}_i}\otimes q_{b_i{b}_t}$把它带入(4)-(6)式可得：

可见，此时需要积分的项就完全和$i$时刻的状态无关了。为了整理公式，把积分相关的项用下面的式子代替:

实际使用中，都是使用离散形式而非连续形式.在解算中，一般采用中值积分方法，即:

那么预积分的离散形式可以表示为:

经过以上的推导，此时状态更新的公式可以整理为:

需要注意的是，陀螺仪和加速度计的模型为:

即认为bias是在变化的，这样便于估计不同时刻的bias值，而不是整个系统运行时间内都当做常值对待。这更符合低精度mems的实际情况。但在预积分时，由于两个关键帧之间的时间较短，因此认为$i$和$j$时刻的bias相等。

需要注意的一点是，预积分的结果中包含了bias，在优化过程中，bias作为状态量也会发生变化，从而引起预积分结果变化。

为了避免bias变化后，重新做预积分，可以把预积分结果在bias处泰勒展开，表达成下面的形式，这样可以根据bias的变化量直接算出新的预积分结果。


其中：

此处暂时不直接给出以上各雅可比的结果，它的推导放在后面进行。

2.连续时间下预积分方差更新矩阵计算

在融合时，需要给不同信息设置权重，而权重由方差得来，因此对于IMU积分，也要计算其方差。我们首先回顾一下连续情况下的微分方程：

方差的计算方式如下：

但需注意的是，此处$F_k$和$G_k$是离散时间下的状态传递方程中的矩阵，而我们一般是在连续时间下推导微分方程，再用它计算离散时间下的传递方程。

2.1 $\delta {\dot{\theta }}_t^{b_k}$的微分推导

为了简便写法，我们把 $\delta {\dot{\theta }}_t^{b_k}$记为$\delta \dot{\theta }$

首先，我们先建立$\delta q$和$\delta \theta$的关系：

所以我们首先要先得到$\delta q$和$\delta \dot{q}$之间的关系。

1) 写出不考虑误差的微分方程

2) 写出考虑误差的微分方程

3) 写出带误差的值与理想值之间的关系

4) 将带误差的值与理想值之间的关系带入2)

其中：

5) 把1)中的关系带入4)

6) 化简方程

首先将5)中的方程移项并左乘$(q_t{)}^{-1}$可得：

又四元数相乘可以转换成矩阵与向量相乘，例如：

我们不妨把$M_p$和$M_p^{\prime }$分别称为左矩阵和右矩阵。分别用$[\ast {]}_L$和$[\ast {]}_R$代替，因此方程可以进一步简化，我们令：

所以，我们可以得到$\delta q$和$\delta \dot{q}$之间的关系:

又根据之前推导的$\delta q$和$\delta \theta$关系：

把它代入上式，又可以得到：

忽略其中的二阶小项，可得：

2.2 $\delta {\dot{\beta }}_t^{b_k}$的微分推导

为了简便写法，我们把 $\delta {\dot{\beta }}_t^{b_k}$记为$\delta \dot{\beta }$

1) 写出不考虑误差的微分方程

2) 写出考虑误差的微分方程

3) 写出带误差的值与理想值之间的关系

4) 将带误差的值与理想值之间的关系带入2)

5) 把1)中的关系带入4)

6) 化简方程

2.3 $\delta {\dot{\alpha }}_t^{b_k}$的微分推导

为了简便写法，我们把 $\delta {\dot{\alpha }}_t^{b_k}$记为$\delta \dot{\alpha }$

1) 写出不考虑误差的微分方程

2) 写出考虑误差的微分方程

3) 写出带误差的值与理想值之间的关系

4) 将带误差的值与理想值之间的关系带入2)

5) 把1)中的关系带入4)

6) 化简方程

3.离散时间下预积分方差更新矩阵计算

得到连续时间微分方程以后，就可以计算离散时间的递推方程了，表示为:

其中：

3.1 $\delta {\theta }_{k+1}$的求解

由于连续时间下有:

则离散时间下应该有:

因此有:

令：

则上式可以重新写为：

3.2 $\delta {\beta }_{k+1}$的求解

由于连续时间下有:

则离散时间下应该有:

把3.1中求得的的$\delta {\theta }_{k+1}$表达式代入上式，可得:

经过一系列合并同类项以后，最终的合并结果为:

由导数形式可以得到递推形式如下:

3.3 $\delta {\alpha }_{k+1}$的求解

由于连续时间下有$\delta \dot{\alpha }=\delta \beta$，则离散时间下应该有:

由导数形式可以写出递推形式:

3.4 矩阵整理

由以上的推导结果，便可以写出$X_{k+1}=F_k{X}_k+G_k{N}_k$中的矩阵:

上面的矩阵中，有:

4.预积分更新

回到bias变化时，预积分结果怎样重新计算的问题，再次给出它的泰勒展开形式：

这里，雅可比没有明确的闭式解，但是在推导方差的更新时，我们得到了：

通过该递推形式，可以知道：

即预积分结果的雅可比，可以通过这种迭代方式计算。

$J_j$中关于bias的项，就是预积分泰勒展开时，各bias对应的雅可比。

5.残差雅可比的推导

在优化时，需要知道残差关于状态量的雅可比。由于已知姿态位姿更新的方法如下:

因此，可以很容易写出一种残差形式如下：

但是和预积分相关的量，仍然与上一时刻的姿态有关，无法直接加减，因此，把残差修正为以下形式：

待优化的变量是:

但在实际使用中，往往都是使用扰动量，因此，实际是对以下变量求雅可比

5.1 姿态残差的雅可比

1) 对$i$时刻姿态误差的雅可比

上式可以化简为：

2) 对$j$时刻姿态误差的雅可比

3) 对$i$时刻陀螺仪bias误差的雅可比

5.2 速度残差的雅可比

1) 对$i$时刻姿态误差的雅可比

2) 对$i$时刻速度误差的雅可比

3) 对$i$时刻加速度bias误差的雅可比