一、基础知识
主要是通过权重分析哪种方案最优,比如去吃饭考虑口味、卫生、价格等等。
1.做成正互反矩阵
矩阵中aij>0,且满足aij*aji=1,如
| O | A | B | C |
| A | 1 | 2 | 5 |
| B | 1/2 | 1 | 2 |
| C | 1/5 | 1/2 | 1 |
里面的数:aij意思是与指标j相比,i的重要程度,(大于1时)越大越重要
如看a12,意思是A比B重要一些。
一般从左下角到右上角的一条线要是都是1会有错误,有兴趣可以自查一下
2.三种求权重方法
把如上面的表格弄成矩阵
2.1算术平均法求权重
%% 方法1:算术平均法求权重
% 第一步:将判断矩阵按照列归一化(每一个元素除以其所在列的和)
Sum_A = sum(A) %列求和
n = size(A,1) %返回行数
SUM_A = repmat(Sum_A,n,1) %弄成n*n矩阵
Stand_A = A ./ SUM_A
% 对应的元素相除即可
% 第二步:将归一化的各列相加
sum(Stand_A,2) % 按行求和
% 第三步:将相加后得到的向量中每个元素 除以n 即可得到权重向量
disp('算术平均法求权重的结果为:');
disp(sum(Stand_A,2) / n)
2.2几何平均法求权重
%% 方法2:几何平均法求权重
% 第一步:将A的元素按照行相乘得到一个新的列向量
clc;A
Prduct_A = prod(A,2)
% prod(A,2)意思是按行每个元素相乘
% 第二步:将新的向量的每个分量 开 n次方(是开方)
Prduct_n_A = Prduct_A .^ (1/n)
% 第三步:对该列向量进行归一化即可得到权重向量
% 将这个列向量中的每一个元素除以这一个向量的和即可
disp('几何平均法求权重的结果为:');
disp(Prduct_n_A ./ sum(Prduct_n_A))2.3特征值和特征向量法(多用)
%% 方法3:特征值法求权重
% 第一步:求出矩阵A的最大特征值以及其对应的特征向量
clc
[V,D] = eig(A) %V是特征向量, D是由特征值构成的对角矩阵(除了对角线元素外,其余位置元素全为0)
Max_eig = max(max(D)) %也可以写成max(D(:))哦~
[r,c] = find(D == Max_eig , 1)
% 找到D中第一个与最大特征值相等的元素的位置,记录它的行和列。
% 第二步:对求出的特征向量进行归一化即可得到我们的权重
V(:,c)
disp('特征值法求权重的结果为:');
disp( V(:,c) ./ sum(V(:,c)) )
3.一致性检验
即计算一致性比例CR,如下图样例
入max即为2.3中的Max_eig,RI表基本是固定的,直接用即可,最后判断一下啊CR是不是小于0.1
%% 计算一致性比例CR
clc
CI = (Max_eig - n) / (n-1);
RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %注意哦,这里的RI最多支持 n = 15
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
disp('因为CR < 0.10,所以该判断矩阵A的一致性可以接受!');
else
disp('注意:CR >= 0.10,因此该判断矩阵A需要进行修改!');
end二、例题实操
1.层次分析法构建评价体系
1.1建立层次结构模型
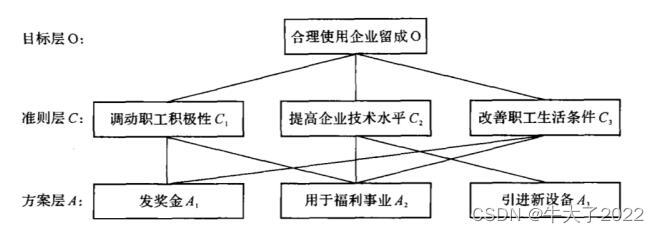
一般得到一个问题,结合条件通过作图软件,如亿图图示,做一个递进层次模型图,如下图
此题是每一个方案都与两个准则层相关,但更多是一个准则对应多个方案考虑,如16国赛题
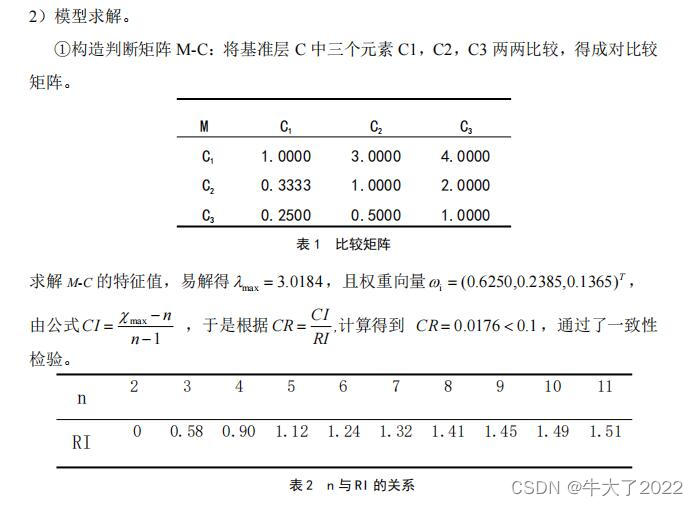
1.2模型求解
接下来就是填表了,一般是网上搜+自己合理的估计,也要符合一开始说的九分制标度法,如:
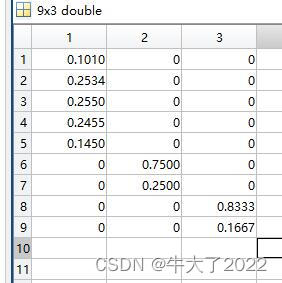
接下来是我们用matlab进行求解,论文中最后只说个结果就行
除了这个矩阵,可以右键工作区,新建一个变量,双击它会进入一个excel类似的界面,输入就行
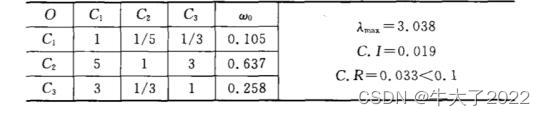
这里用2.3特征值和特征向量法求权重,求出权重和入max
权重向量想更严谨点可以三种方法都求,最后取平均值,最后检验一下一致性
计算过程是繁琐的,最后结果在论文呈现一般比较简介,如:
16年国赛
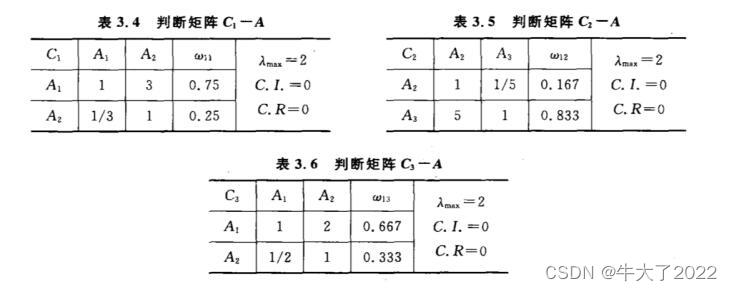
同上面方法,把每个准则对应的方案进行判断
由此可以计算P 层每个影响因素所占的总权重 ,矩阵相乘即可(线代特点,注意乘的顺序)
像国赛那种一个准则对应多个方案
1.3模型结论与分析
根据上面求的W2,论文写写那个更重要就行(正经比赛没那么简单,只是演示)