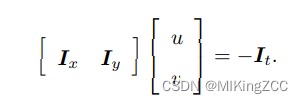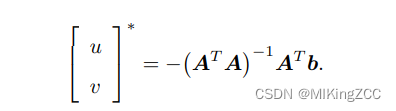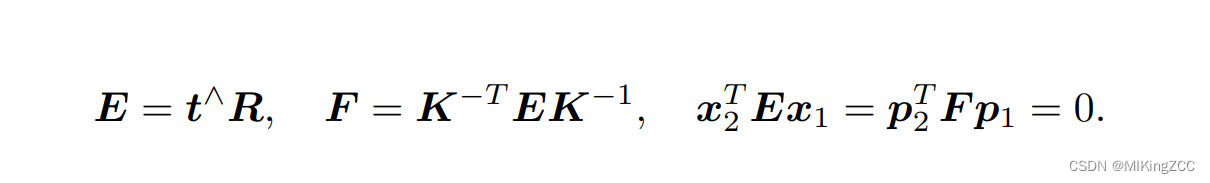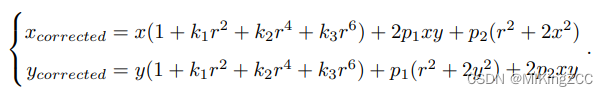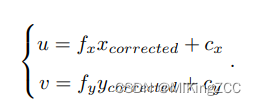一、坐标系定义

1. 相机坐标系（右手系）：X轴朝右，Y轴朝下，Z轴朝前 。
2. MU坐标系（右手系）：X轴朝前，Y轴朝左，Z轴朝上。
3. 世界坐标系：在VINS中没有先验地图，通常把第一帧作为世界坐标系的原点，相机是6自由度不可观的，所以在没有IMU信息时，把平移设置成$(0,0,0)$,把旋转设置成单位阵。在VINS中，IMU可以感受到重力信息，所以将Z轴与重力方向对齐，得到roll、pitch的初始值，而仅仅将yaw设置为0。

二、图像选择，控制发送

在VINS中相机的频率为30HZ，IMU的频率为100HZ，但是feature_tracker节点发送给vins_estimator节点的频率控制在10HZ。由于VINS前端使用的光流法，没有描述子匹配，图像时间戳差太多有可能会导致光流追踪失败。所以每帧图像检查时间戳是否正常，这里认为超过一秒或者错乱就异常：

img_msg->header.stamp.toSec() - last_image_time > 1.0 || img_msg->header.stamp.toSec() < last_image_time

一旦发生时间戳混乱，直接reset，并发布重启消息：

pub_restart.publish(restart_flag); 

控制前端发送给后端的频率：

if (round(1.0 * pub_count / (img_msg->header.stamp.toSec() - first_image_time)) <= FREQ)  

为了防止基数$\Delta t$过大，导致如果短时间内发送过多，但是计算不敏感的情况发生，重启一下计数：

if (abs(1.0 * pub_count / (img_msg->header.stamp.toSec() - first_image_time) - FREQ) < 0.01 * FREQ)
{
    first_image_time = img_msg->header.stamp.toSec();
    pub_count = 0;
}

VINS前端给后端发送了去畸变的归一化相机坐标系坐标、像素坐标、特征点id以及归一化坐标下的速度。
定义发送的消息：

sensor_msgs::PointCloudPtr feature_points(new sensor_msgs::PointCloud);
feature_points->header = img_msg->header;
feature_points->header.frame_id = "world";

封装追踪数大于1特征点（因为等于1没法构成重投影约束，也没法三角化）的数据：

 if (trackerData[i].track_cnt[j] > 1)
 {
     int p_id = ids[j];
     hash_ids[i].insert(p_id);   // 这个并没有用到
     geometry_msgs::Point32 p;
     p.x = un_pts[j].x;
     p.y = un_pts[j].y;
     p.z = 1;
     // 利用这个ros消息的格式进行信息存储
     feature_points->points.push_back(p);
     id_of_point.values.push_back(p_id * NUM_OF_CAM + i);
     u_of_point.values.push_back(cur_pts[j].x);
     v_of_point.values.push_back(cur_pts[j].y);
     velocity_x_of_point.values.push_back(pts_velocity[j].x);
     velocity_y_of_point.values.push_back(pts_velocity[j].y);
 }

发布：

pub_img.publish(feature_points);

三、图像均衡化，光流追踪

1. 图像自适应均衡化

当图像太暗或者太亮时，提取特征点比较难，通常将图像预处理，进行自适应的局部直方图均衡化

/*
createCLAHE类参数说明：
clipLimit：颜色对比度的阈值，可选项，默认值 8
titleGridSize：局部直方图均衡化的模板（邻域）大小，可选项，默认值 (8,8)
*/
cv::Ptr<cv::CLAHE> clahe = cv::createCLAHE(3.0, cv::Size(8, 8));
TicToc t_c;
clahe->apply(_img, img);
ROS_DEBUG("CLAHE costs: %fms", t_c.toc());

2. 光流追踪

调用opencv函数进行光流追踪，同时通过opencv光流追踪给的状态位剔除outlier。

/*
calcOpticalFlowPyrLK函数 实现了金字塔中Lucas-Kanade光流的稀疏迭代版本
*/
cv::calcOpticalFlowPyrLK(cur_img, forw_img, cur_pts, forw_pts, status, err, cv::Size(21, 21), 3);

参数介绍：

void cv::calcOpticalFlowPyrLK	(	
InputArray 	prevImg, //以该图片为基准流追踪，前一帧图像
InputArray 	nextImg, //用来获得追踪结果的图片，当前帧图像
InputArray 	prevPts, //,以该数组点为基准进行流追踪，单位单精度浮点数，即前一帧特征点
InputOutputArray 	nextPts, //获得前一帧特征点 在当前帧追踪点的结果
OutputArray 	status,   //输出状态标记，如果追踪到了结果，则对应同角标的状态向量位置元素为1，否则为0
OutputArray 	err,      //输出错误标记
Size 	winSize = Size(21, 21),  //每个金字塔的搜索窗口的winSize大小
int 	maxLevel = 3,     //金字塔层数，图像层级总数为该值＋1
TermCriteria 	criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 0.01),
int 	flags = 0,
double 	minEigThreshold = 1e-4 
)		

在 LK光流中，我们认为来自相机的图像是随时间变化的。图像可以看作时间的函数：$I(t)$。那么，一个在 $t$ 时刻，位于 $(x,y)$ 处的像素，它的灰度可以写成$I(x,y,t)$。这种方式把图像看成了关于位置与时间的函数，它的值域就是图像中像素的灰度。现在考虑某个固定的空间点，它在 $t$ 时刻的像素坐标为 $x$, $y$。由于相机的运动，它的图像坐标将发生变化。我们希望估计这个空间点在其他时刻里图像的位置。
灰度不变假设：同一个空间点的像素灰度值，在各个图像中是固定不变的。对于 $t$ 时刻位于 $(x,y)$ 处的像素，我们设 $t+dt$ 时刻，它运动到 $(x+dx,y+dy)$ 处。由于灰度不变，我们有：
$$I(x+dx,y+dy,t+dt)=I(x,y,t)$$
对左边进行泰勒展开，保留一阶项，得:
$$I(x+dx,y+dy,t+dt)\approx I(x,y,t)+\frac{\partial I}{\partial x}dx+\frac{\partial I}{\partial y}dy+\frac{\partial I}{\partial t}dt$$
因为我们假设了灰度不变，于是下一个时刻的灰度等于之前的灰度，从而:
$$\frac{\partial I}{\partial x}dx+\frac{\partial I}{\partial y}dy+\frac{\partial I}{\partial t}dt=0$$
两边除以 $dt$，得：
$$\frac{\partial I}{\partial x}\frac{dx}{dt}+\frac{\partial I}{\partial y}\frac{dy}{dt}=-\frac{\partial I}{\partial t}$$
其中 $dx/dt$ 为像素在 $x$ 轴上运动速度，而 $dy/d$t 为 $y$ 轴速度，把它们记为 $u,v$。同时 $\partial I/\partial x$ 为图像在该点处 $x$ 方向的梯度，另一项则是在 $y$ 方向的梯度，记为 $Ix,Iy$。写成矩阵形式，有：

我们想计算的是像素的运动 $u,v$，但是该式是带有两个变量的一次方程，仅凭它无法计算出 $u,v$。因此，必须引入额外的约束来计算$u,v$。在 LK 光流中，我们假设某一个窗口内的像素具有相同的运动。
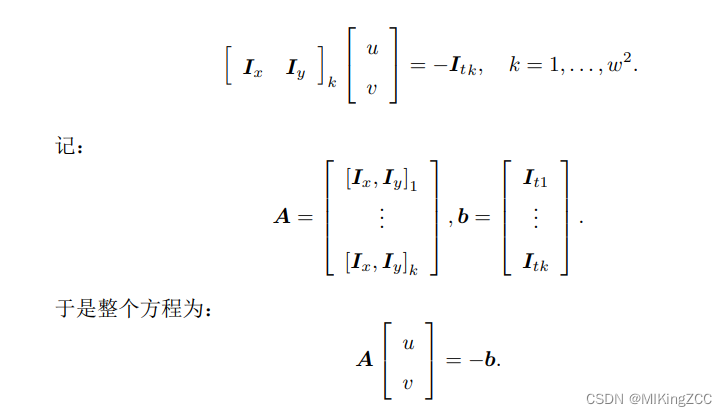
考虑一个大小为 $w\times w$ 大小的窗口，它含有 $w^2$ 数量的像素。由于该窗口内像素具有同样的运动，因此我们共有 $w^2$ 个方程：

这是一个关于 u, v 的超定线性方程，传统解法是求最小二乘解。最小二乘在很多时候都用到过：

四、剔除外点

1. 通过图像边界和追踪状态位剔除outlier

for (int i = 0; i < int(forw_pts.size()); i++)
    // Step 2 通过图像边界剔除outlier
    if (status[i] && !inBorder(forw_pts[i]))    // 追踪状态好检查在不在图像范围
        status[i] = 0;
//此时status中为0的情况既包括未追踪到的点也包括图像外的点
reduceVector(prev_pts, status); // 没用到
reduceVector(cur_pts, status);
reduceVector(forw_pts, status);
reduceVector(ids, status);  // 特征点的id
reduceVector(cur_un_pts, status);   // 去畸变后的坐标
reduceVector(track_cnt, status);    // 追踪次数

reduceVector使用双指针实现了一个空间复杂度为$o(1)$，时间复杂度为$o(n)$的vector缩减算法。

2. 通过对极约束剔除outlier

首先将上一帧特征点的cur_pts以及当前帧的特征点forw_pts从 像素坐标系转换到归一化坐标系，然后将归一化坐标投影到一个虚拟相机的像素坐标系，这样虽然对精度可能有一定影响，但是好处就是在计算基础矩阵时F_THRESHOLD的设定与真实的相机无关，节省了一些复杂的判定。
VINS中调用了OpenCV中的基础矩阵计算函数，但是只是利用status来对outlier进行剔除。

//返回值是一个Mat矩阵
cv::findFundamentalMat(un_cur_pts, un_forw_pts, cv::FM_RANSAC, F_THRESHOLD, 0.99, status);

关于findFundamentalMat函数的一些介绍：

CV_EXPORTS_W Mat findFundamentalMat( InputArray points1, //第一张图像特征点的vector
									 InputArray points2,//第二张图像匹配特征点的vector
                                     int method = FM_RANSAC,//OpenCV中提供四个求解对极约束的方法 7点法、8点法、RANSAC算法、LMedS算法
                                     double param1 = 3, // 用于 RANSAC 的参数。 它是从一个点到一条以像素为单位的对极线的最大距离，超过该距离的点被认为是异常值，不用于计算最终的基本矩阵。 它可以设置为 1-3 之类的值，具体取决于点定位的准确性、图像分辨率和图像噪声。
                                     double param2 = 0.99, //该参数仅仅在RANSAC算法以及LMedS算法中， 它指定了估计矩阵正确的期望置信度（概率）
                                     OutputArray mask = noArray() //输出包含 status数组，其中的每个元素对于异常值都设置为 0，对于其他点设置为 1。 该数组仅在 RANSAC 和 LMedS 方法中计算。 对于其他方法，它设置为全 1
                                     );

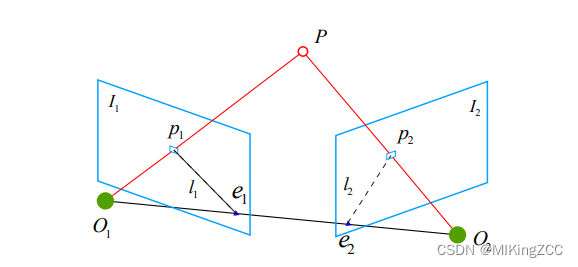
关于对极约束的的一些介绍：
当我们希望求取两帧图像 $I1,I2$ 之间的运动，设第一帧到第二帧的运动为$R,t$。两个相机中心分别为 $O1,O2$。现在，考虑 $I1$ 中有一个特征点 $p1$，它在 $I2$ 中对应着特征点 $p2$。它们是通过特征匹配得到的。如果匹配正确，说明它们确实是同一个空间点在两个成像平面上的投影。这里我们需要一些术语来描述它们之间的几何关系。首先，连线 $O_1{P}_1$ 和连线$O_2{P}_2$ 在三维空间中会相交于点 $P$。这时候点 $O1,O2,P$ 三个点可以确定一个平面，称为极平面（Epipolar plane）。$O_1{O}_2$ 连线与像平面 $I1,I2$ 的交点分别为 $e1,e2$，称为极点（Epipoles），$O_1{O}_2$ 被称为基线（Baseline）。称极平面与两个像平面 $I1,I2$ 之间的相交线 $l1,l2$ 为极线（Epipolar line）。

对极约束，的几何意义是 $O_1,P,O_2$ 三者共面。对极约束中同时包含了平移和旋转。我们把中间部分记作两个矩阵：基础矩阵（Fundamental Matrix）$F$ 和本质矩阵（Essential Matrix）$E$ ($E$ 和 $F$ 只相差了相机内参)，可以进一步简化对极约束（并可以通过求解超定方程得到$E$和$F$）：

• 本质矩阵是由对极约束定义的。由于对极约束是等式为零的约束，所以对 $E$ 乘以任意非零常数后，对极约束依然满足。我们把这件事情称为 $E$ 在不同尺度下是等价的。
• 根据 $E=t\wedge R$，可以证明 [3]，本质矩阵 E 的奇异值必定是 $[\sigma ,\sigma ,0{]}^T$ 的形式。这称为本质矩阵的内在性质。
• 另一方面，由于平移和旋转各有三个自由度，故$t\wedge R$ 共有六个自由度。但由于尺度等价性，故 $E$ 实际上有五个自由度。$F$的自由度为7。

五、特征点均匀化、提取新的特征点

1. 特征点均匀化

对当前所有特征点进行排序，利用光流特点，追踪次数多的稳定性好，排前面

vector<pair<int, pair<cv::Point2f, int>>> cnt_pts_id;
sort(cnt_pts_id.begin(), cnt_pts_id.end(), [](const pair<int, pair<cv::Point2f, int>> &a, const pair<int, pair<cv::Point2f, int>> &b)
{
   return a.first > b.first;
});

定义一个mask矩阵，初始化所有值为255，遍历特征点，把周围一个圆内全部置0,这个区域不允许别的特征点存在，避免特征点过于集中。

for (auto &it : cnt_pts_id)
{
    if (mask.at<uchar>(it.second.first) == 255)
    {
        // 把挑选剩下的特征点重新放进容器
        forw_pts.push_back(it.second.first);
        ids.push_back(it.second.second);
        track_cnt.push_back(it.first);
        // opencv函数，把周围一个圆内全部置0,这个区域不允许别的特征点存在，避免特征点过于集中
        cv::circle(mask, it.second.first, MIN_DIST, 0, -1);
    }
}

2. 提取新的特征点

在VINS中提取特征点是使用的OpenCV中的goodFeaturesToTrack函数，该可以计算Harris角点和shi-tomasi角点，但默认情况下计算的是shi-tomasi角点。
只有发布时才会提取更多特征点，同时避免提的点进mask；当然新提取得到的点可能会出现过于集中的情况，但是，他们在下一次进入时就会进行均匀化处理。

cv::goodFeaturesToTrack(forw_img, n_pts, MAX_CNT - forw_pts.size(), 0.01, MIN_DIST, mask);

关于goodFeaturesToTrack函数的参数介绍：

void cv::goodFeaturesToTrack( InputArray _image,//8位或32位单通道灰度图像；
							  OutputArray _corners,//保存检测出的角点vector
                              int maxCorners, //定义可以检测到的角点的数量的最大值，如果实际检测的角点超过此值，则只返回前maxCorners个强角点
                              double qualityLevel,//检测到的角点的质量等级，角点特征值小于qualityLevel*最大特征值的点将被舍弃
                              double minDistance,//两个角点间最小间距，以像素为单位；
                              InputArray _mask, //指定检测区域，若检测整幅图像，mask置为空Mat()；
                              int blockSize, //计算协方差矩阵时的窗口大小
                              bool useHarrisDetector,  //指示是否使用Harris角点检测，如不指定，则计算shi-tomasi角点
                              double harrisK 
                              )

对于新提取的特征点索引，先全部赋值为-1：

// 把新的点加入容器，id给-1作为区分
void FeatureTracker::addPoints()
{
    for (auto &p : n_pts)
    {
        forw_pts.push_back(p);
        ids.push_back(-1);
        track_cnt.push_back(1);
    }
}

然后再统一递增索引，越界就返回false（这一步在去除畸变、计算像素速度之后）。

bool FeatureTracker::updateID(unsigned int i)
{
    if (i < ids.size())
    {
        if (ids[i] == -1)
            ids[i] = n_id++;
        return true;
    }
    else
        return false;
}

六、去除畸变、计算像素速度

将特征点投影到归一化平面，并去畸变：
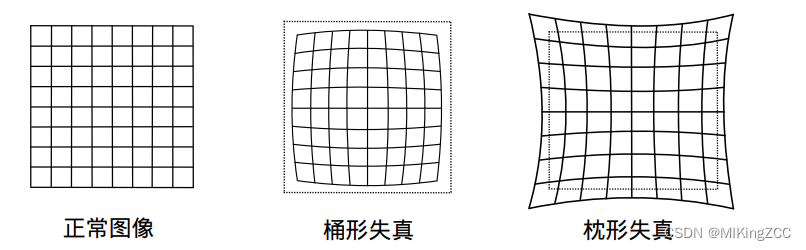
由透镜形状引起的畸变称之为径向畸变。在针孔模型中，一条直线投影到像素平面上还是一条直线。可是，在实际拍摄的照片中，摄像机的透镜往往使得真实环境中的一条直线在图片中变成了曲线。越靠近图像的边缘，这种现象越明显。由于实际加工制作的透镜往往是中心对称的，这使得不规则的畸变通常径向对称。它们主要分为两大类，桶形畸变和枕形畸变。在这两种畸变中，穿过图像中心和光轴有交点的直线还能保持形状不变。
除了透镜的形状会引入径向畸变外，在相机的组装过程中由于不能使得透镜和成像面严格平行也会引入切向畸变。

对于相机坐标系中的一点 $P(X,Y,Z)$，我们能够通过五个畸变系数$k_1、k_2、k_3、p_1、p_2$找到这个点在像素平面上的正确位置:

1. 将三维空间点投影到归一化图像平面。设它的归一化坐标为 $[x,y{]}^T$。
2. 对归一化平面上的点进行径向畸变和切向畸变纠正。
3. 将纠正后的点通过内参数矩阵投影到像素平面，得到该点在图像上的正确位置。
   但是我们通常是已知一个畸变后的点坐标的像素值，要得到一个正常图像的点坐标的像素值，观察上述方程，想通过$(x_{correted},y_{correted})$反解得到正确的$(x,y)$是困难的。如果是对一整张图像进行处理，一种普遍的做法是建立畸变点坐标和正常点坐标的映射关系（遍历正常点坐标得到畸变点坐标，此时正常点坐标的像素就可以通过畸变点坐标像素插值得到）。
   但是在VINS中没有对一整张图进行去畸变处理，为了加快速度，只对提取出来的特征点进行去畸变处理，采用的是逐渐逼近的思想。

 m_camera->liftProjective(a, b);
 cur_un_pts.push_back(cv::Point2f(b.x() / b.z(), b.y() / b.z()));
 // id->坐标的map
 cur_un_pts_map.insert(make_pair(ids[i], cv::Point2f(b.x() / b.z(), b.y() / b.z())));

在liftProjective函数中：
先将像素坐标投影到归一化相机坐标系：
$$\begin{gathered} \frac{X}{Z}=\frac{u}{f_x}-\frac{c_x}{f_x} \\ \frac{Y}{Z}=\frac{v}{f_y}-\frac{c_y}{f_y} \end{gathered}$$

/*  提前计算
    m_inv_K11 = 1.0 / mParameters.gamma1();
    m_inv_K13 = -mParameters.u0() / mParameters.gamma1();
    m_inv_K22 = 1.0 / mParameters.gamma2();
    m_inv_K23 = -mParameters.v0() / mParameters.gamma2();
*/    
    mx_d = m_inv_K11 * p(0) + m_inv_K13;
    my_d = m_inv_K22 * p(1) + m_inv_K23;

对点去畸变的做法（思想：逐渐逼近）如下：
（1） 假设当前的畸变点是正常点，求解该点对应的畸变点，得到$\Delta u$ (假设正常点坐标+$\Delta u$=对应畸变点坐标)
（2） 由于当前点实际上是一个畸变点，所以使用 畸变点-$\Delta u=$一个新的畸变点，虽然新计算出来的点可能仍然存在畸变，但是一定比原来的畸变点更接近正常点。
（3） 将新计算得到的点重复（1）、（2）过程，逐渐逼近正常点。
值得注意的是，由于越靠近边缘畸变越大，所以计算出来的第一次计算出来的$\Delta u$一定小于实际的差值，而且逼近过程中$\Delta u$逐渐减小。

 Eigen::Vector2d d_u;
 // 这里mx_d + du = 畸变后
 distortion(Eigen::Vector2d(mx_d, my_d), d_u);
 // Approximate value
 mx_u = mx_d - d_u(0);
 my_u = my_d - d_u(1);

 for (int i = 1; i < n; ++i)
 {
     distortion(Eigen::Vector2d(mx_u, my_u), d_u);
     mx_u = mx_d - d_u(0);
     my_u = my_d - d_u(1);
 }

像素速度的计算是为了用来后续时间戳标定，手段是遍历当前所有的特征点（要求id不为-1.-1表示是当前帧新提取的特征点，在上一帧中没有对应点，新特征点的速度设置为0），在上一帧的特征点中寻找id相同的点，计算像素速度，若没有找到则速度设置为0：

if (!prev_un_pts_map.empty())
{
   //计算两帧之间的时间差
   double dt = cur_time - prev_time;
   pts_velocity.clear();
   for (unsigned int i = 0; i < cur_un_pts.size(); i++)
   {
   	    //判断是不是新特征点
       if (ids[i] != -1)
       {
           std::map<int, cv::Point2f>::iterator it;
           it = prev_un_pts_map.find(ids[i]);
           // 找到同一个特征点
           if (it != prev_un_pts_map.end())
           {
               double v_x = (cur_un_pts[i].x - it->second.x) / dt;
               double v_y = (cur_un_pts[i].y - it->second.y) / dt;
               // 得到在归一化平面的速度
               pts_velocity.push_back(cv::Point2f(v_x, v_y));
           }
           else
               pts_velocity.push_back(cv::Point2f(0, 0));
       }
       else
       {
           pts_velocity.push_back(cv::Point2f(0, 0));
       }
   }
}

如果当前帧是第一帧，则所有特征点速度全部设置为0。

七、关于光流法和特征点法的一点说明

VINS中使用LK光流实现了帧间匹配，在另一个优秀的开源框架ORB-SLAM中使用了特征点法。对于每帧图像，光流法相比较于特征点法，提取的特征点更少，无需计算和匹配描述子，但是需要进行光流追踪，要求相机运动较平滑，采样频率较高。在LK光流中金字塔使用的计算可能会增加一点计算时间，但是整体而言，光流法在进行帧间匹配时，无论耗时还是鲁棒性都是强于特征点匹配的方法，但是在全局一致性的重定位以及回环检测中特征点法有着光流法无法代替的作用。