面试题4：二维数组中的查找

题目：

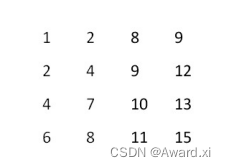
在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

例如下面的二维数组就是每行、每列都递增排序。如果在这个数组中查找数字7，则返回true；如果查找数字5，由于数组不含有该数字，则返回false。

思路：

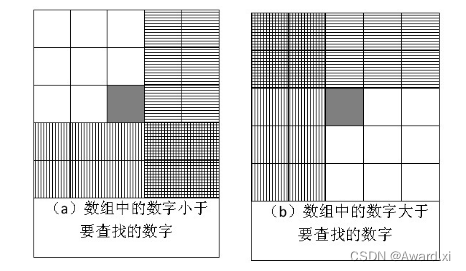
固有思路，就是在用对角线找元素，当数组中选取的数字刚好和要查找的数字相等时，就结束查找过程。如果选取的数字小于要查找的数字，那么根据数组排序的规则，要查找的数字应该在当前选取位置的右边或者下边，如图（a）所示。同样，如果选取的数字大于要查找的数字，那么要查找的数字应该在当前选取位置的上边或者左边，如图（b）所示。

这样做起来考虑复杂度很高，因为他一下就由两个区域部分了，并且还有重复的。

题解：

当我们需要解决一个复杂的问题时，一个很有效的办法就是从一个具体的问题入手，通过分析简单具体的例子，试图寻找普遍的规律。

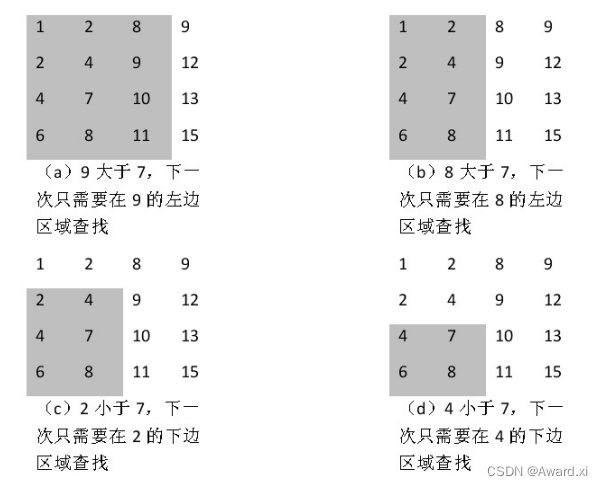
我们用查找7这个元素为例：

我们优先从右上角选取元素9，大于7则它下面的一列全是大于7的可以去掉，再选取右上角元素8，它也是大于7的则这一列可以去掉，再选取右上角元素2，它大于7则这一行去掉，再选取右上角数据为4，也是小于7的，则去掉一行，在选取右上角元素为7则，找到该元素了。如下：

程序代码如下：

bool Find(vector<vector<int>>& matrix,int number){
    int rows = matrix.size();	//行
    int columns = matrix[0].size();	//列
    
    //选取最右侧元素
    int row = 0;
    int column = column-1;
    while(row < rows && column >= 0){
        if(matrix[row][columns] > number)
            columns--;
        else if(matrix[row][colums] < number)
            rows++;
        else 
            return true;
    }
    
    return false;
}

注：在前面的分析中，我们每次都选取数组查找范围内的右上角数字。同样，我们也可以选取左下角的数字。但我们不能选择左上角数字或者右下角数字。以左上角数字为例，最初数字1位于初始数组的左上角，由于1小于7，那么7应该位于1的右边或者下边。此时我们既不能从查找范围内剔除1所在的行，也不能剔除1所在的列，这样我们就无法缩小查找的范围。

本题考点：

考查对二维数组的理解及编程能力。二维数组在内存中占据连续的空间。在内存中从上到下存储各行元素，在同一行中按照从左到右的顺序存储。因此我们可以根据行号和列号计算出相对于数组首地址的偏移量，从而找到对应的元素。

考查分析问题的能力。当发现问题比较复杂时，能不能通过具体的例子找出其中的规律，是能否解决这个问题的关键所在。这个题目只要从一个具体的二维数组的右上角开始分析，就能找到查找的规律，从而找到解决问题的突破口。