数据结构与算法题目集PTA
6-1 单链表逆转
注意审题,是对原表进行改变,而不是创建一个新表进行逆值。所以逆值后输出原表时,直接输出尾节点。
List Reverse( List L ){
List s,head = (struct Node*)malloc(sizeof(struct Node));
head->Next = NULL;
while( L!= NULL){
s = L->Next;
L->Next = head->Next;
head->Next = L;
L = s;
}
return head->Next;
}
6-2 顺序表操作集
链接中的代码,我加了测试环节可以下载测试一下
创建空表,Last初始值为-1 //Last 指向的是数组中的最后一个元素的下标,并非长度
List MakeEmpty(){
List L;
L = (struct LNode*)malloc(sizeof(struct LNode));
L->Last = -1;
return L;
}
// 返回线性表中X的位置。若找不到则返回ERROR;
Position Find( List L, ElementType X ){
for(int i=0;i<=L->Last;i++){
if(L->Data[i] == X){
return i;
}
}
return ERROR;
}
// 插入操作
bool Insert( List L, ElementType X, Position P ){
if(L->Last == MAXSIZE-1){
printf("FULL");
return false;
}
else if( P < 0 || P > L->Last+1){
printf("ILLEGAL POSITION");
return false;
}
else{
for(int i=L->Last;i>=P;i--){
L->Data[i+1] = L->Data[i];
}
L->Data[P] = X;
L->Last++;
}
return true;
}
// 删除操作
bool Delete( List L, Position P ){
if( P < 0 || P > L->Last){
printf("POSITION %d EMPTY",P);
return false;
}
for(int i=P;i<L->Last;i++){ //表长为0时,不仅循环直接减,变成-1
L->Data[i] = L->Data[i+1];
}
L->Last--;
return true;
}
6-3 求链式表的表长
采用头插法,不带头节点
读表,
没有啥难度,不做解释了
List Read(){
List head, s;
ElementType data;
head = NULL;
scanf("%d",&data);
while(data != -1){
s = (struct LNode*)malloc(sizeof(struct LNode));
s->Data = data;
s->Next = head;
head = s;
scanf("%d",&data);
}
return head;
}
// 计算表长度
int Length( List L ){
int sum = 0;
while(L != NULL){
sum++;
L = L->Next;
}
return sum;
}
6-4 链式表的按序号查找
读表,采用尾插法,不带头节点
List Read(){
List head,rear,s,temp; // head头节点 rear尾结点 s插入节点
int data;
scanf("%d", &data); //因为不带头节点所以头节点要特殊判断
if(data == -1){ //表空
return NULL;
}
head = (struct LNode*)malloc(sizeof(struct LNode));
head->Data = data;
rear = head;
scanf("%d", &data);
while(data != -1){
s = (struct LNode*)malloc(sizeof(struct LNode));
s->Data = data;
rear->Next = s;
rear = s;
scanf("%d", &data);
}
rear->Next = NULL; // 最后一个节点加空NUll
temp = head;
while(temp != NULL){
printf(" %d ",temp->Data);
temp = temp->Next;
}
printf("\n");
return head;
}
// 查找元素
注意K的取值范围,注意L是否为空
ElementType FindKth( List L, int K ){
if(K <= 0){
return ERROR;
}
while(K>1&& L!=NULL){
L = L->Next;
K--;
}
if(L == NULL){
return ERROR;
}
return L->Data;
}
6-5 链式表操作集
查找函数-------返回线性表中首次出现X的位置。若找不到则返回ERROR
Position Find( List L, ElementType X ){
while(L != NULL){
if(L->Data == X){
return L;
}
L = L->Next;
}
return ERROR;
}
插入函数-----将X插入在位置P指向的结点之前,返回链表的表头
如果参数P指向非法位置,则打印“Wrong Position for Insertion”,返回ERROR;
List Insert( List L, ElementType X, Position P ){
Position s,rear = L;
if(L == NULL && P == NULL){ //表空时,插入第一个节点
L = (struct LNode*)malloc(sizeof(struct LNode));
L->Data = X;
L->Next = NULL;
return L;
}
if(L == P){ // 头节点插入
s = (struct LNode*)malloc(sizeof(struct LNode));
s->Data = X;
s->Next = L;
L = s;
return L;
}
while(rear != NULL){
if(rear->Next == P){
s = (struct LNode*)malloc(sizeof(struct LNode));
s->Data = X;
s->Next = P;
rear->Next = s;
return L;
}
rear = rear->Next;
}
printf("Wrong Position for Insertion\n");
return ERROR;
}
删除函数----- 将位置P的元素删除并返回链表的表头
若参数P指向非法位置,则打印“Wrong Position for Deletion”并返回ERROR
List Delete( List L, Position P ){
Position head = L,rear = head->Next;
if(P != NULL){ // P 节点有值时
if(L == P){ // 第一个节点时,直接删除
return L->Next;
}
while(rear != NULL){ //删除指定节点,设置2个指针,一个指向P,一个指向P的前节点
if( rear == P){
head->Next = rear->Next;
free(rear);
return L;
}
head = head->Next;
rear = rear->Next;
}
}
printf("Wrong Position for Deletion\n");
return ERROR;
}
6-6 带头结点的链式表操作集
创建并返回一个空的线性表
List MakeEmpty(){
List head;
head = (struct LNode *)malloc(sizeof(struct LNode));
head->Next = NULL;
return head;
}
返回线性表中X的位置。若找不到则返回ERROR
Position Find( List L, ElementType X ){
Position head = L->Next; // 第一个节点
while(head != NULL){
if(head->Data == X){
return head;
}
head = head->Next;
}
return ERROR;
}
将X插入在位置P指向的结点之前,返回true ****还是头插法****
如果参数P指向非法位置,则打印Wrong Position for Insertion返回false
bool Insert( List L, ElementType X, Position P ){
Position s,rear = L;
if(L->Next == NULL && P == NULL){ //插入第1个节点
s = (struct LNode*)malloc(sizeof(struct LNode));
s->Data = X;
s->Next = NULL;
L->Next = s;
return true;
}
while(rear != NULL){ //设置1个指针,rear->next指针比较,相等时,将新结点插入rear后 rear->next之前
if(rear->Next == P){
s = (struct LNode*)malloc(sizeof(struct LNode));
s->Data = X;
rear->Next = s;
s->Next = P;
return true;
}
rear = rear->Next;
}
printf("Wrong Position for Insertion\n");
return false;
}
将位置P的元素删除并返回true。
若参数P指向非法位置,则打印Wrong Position for Deletion并返回false
bool Delete( List L, Position P ){
Position head=L,rear = L->Next;
if(P != NULL){
while(rear != NULL){ //设置两个指针 1前1后,后面的指针比较,相等时,删除后结点,连接后后结点
if(rear == P){
head->Next = rear->Next;
free(P);
return true;
}
head = head->Next;
rear = rear->Next;
}
}
printf("Wrong Position for Deletion\n");
return false;
}
6-7 在一个数组中实现两个堆栈
共享栈
不要粗心大意,千万要小心,题目的要求
1.数组为空的情况、2.两个栈的设置、3.栈满、栈空的设置
PTA的审题标准不是很严,所以没有考虑到代码的健壮性,如果你想当你一名合格的程序猿,就要去考虑,可能出错的情况。
我附加了测试的代码,可以看一下,不过输入方式和pta不同,自行分析。不难
这里和PTA上给的代码不同,不能按样例输入,自行看代码,此代码不难
Operation GetOp(){
int n;
while(1){
printf("1.PUSH 2.POP 3.END,请输入代码:\n");
scanf("%d",&n);
switch (n) {
case 1:
return push;
case 2:
return pop;
case 3:
return end;
}
printf("输入错误!\n");
}
}
// 打印输出 指定栈
void PrintStack( Stack S, int Tag ){
int n;
if(Tag == 1){
n = S->Top1;
printf("Pop from Stack %d:",Tag);
while(n >= 0){
printf(" %d",S->Data[n]);
n--;
}
}
else if(Tag == 2){
n = S->Top2;
printf("Pop from Stack %d:",Tag);
while(n < S->MaxSize){
printf(" %d",S->Data[n]);
n++;
}
}
printf("\n");
}
Stack CreateStack( int MaxSize ){ //两个栈,分别在数组两端
Stack s;
if(MaxSize <= 0){
return NULL;
}
s = (struct SNode*)malloc(sizeof(struct SNode));
s->Data = (ElementType*)malloc(sizeof(ElementType)*MaxSize);
s->Top1 = -1;
s->Top2 = MaxSize;
s->MaxSize = MaxSize;
return s;
}
// 入栈------S 为空时要考虑
bool Push( Stack S, ElementType X, int Tag ){
if(S == NULL){ // 这里我没想到,所以一定要注意细节
return false;
}
if(S->Top2 - S->Top1 == 1){ // 栈满
printf("Stack Full\n");
return false;
}
if(Tag == 1){
S->Top1++;
S->Data[S->Top1] = X;
}else if(Tag == 2){
S->Top2--;
S->Data[S->Top2] = X;
}
return true;
}
// 出栈
ElementType Pop( Stack S, int Tag ){
ElementType temp;
if(S == NULL){ //注意栈空的情况
return ERROR;
}
if(Tag == 1 ){
if(S->Top1 == -1){
printf("Stack %d Empty\n",Tag);
return ERROR;
}
temp = S->Data[S->Top1];
S->Top1--;
return temp;
}
else if(Tag == 2){
if(S->Top2 == S->MaxSize){
printf("Stack %d Empty\n",Tag);
return ERROR;
}
temp = S->Data[S->Top2];
S->Top2++;
return temp;
}
return ERROR;
}
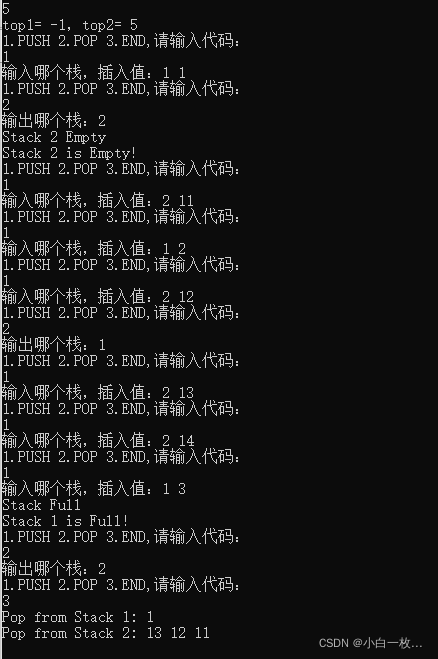
最后附上效果图:
6-8 求二叉树高度
递归查找 ,返回左右子树中更深的
int GetHeight( BinTree BT ){
int h1 = 0;
int h2 = 0;
if(!BT)
return 0;
else{
h1 = GetHeight(BT->Left);
h2 = GetHeight(BT->Right);
if(h1>h2)
return ++h1;
else
return ++h2;
}
}
6-9 二叉树的遍历
6-10 二分查找
插入数据的函数:不要求
List ReadInput(){
int n,i = 0,data;
List L = (struct LNode*)malloc(sizeof(struct LNode));
L->Last = 0; // 一开始值为空
printf("你想要几个数并创建多大的数组:");
scanf("%d",&n);
while(n--){
scanf("%d",&data);
i = L->Last;
while(i>=1){
if(data < L->Data[i]){ // 直接插入排序
L->Data[i+1] = L->Data[i];
i--;
}
else
break;
}
i++;
L->Data[i] = data;
L->Last++;
}
/*
查看插入是否正确
*/
for(int i=1;i<=L->Last;i++){
printf(" %d ",L->Data[i]);
}
printf("\n");
return L;
}
Position BinarySearch( List L, ElementType X ){
int head = 1, rear = L->Last;
while(head <= rear){ // head <= rear 查找
if(X == L->Data[(head+rear)/2]){ //中间比较 相等返回
return (head+rear)/2;
}
else if(X < L->Data[(head+rear)/2]){ // 小于上半部分
rear = (head+rear)/2-1;
}
else { // 大于上半部分
head = (head+rear)/2+1;
}
}
return NotFound;
}
6-11 先序输出叶结点
void PreorderPrintLeaves( BinTree BT ){
if(BT != NULL){
if(BT->Left == NULL && BT->Right == NULL) // 叶节点输出
printf(" %c",BT->Data);
if(BT->Left != NULL) // 左孩子-非叶节点递归,向下查找叶节点
PreorderPrintLeaves(BT->Left);
if(BT->Right != NULL) // 右孩子-非叶节点递归,向下查找叶节点
PreorderPrintLeaves(BT->Right);
}
}
6-12 二叉搜索树的操作集
停更22-6-10—22-11-27日-工作后的感触
刚毕业,找的工作比较不理想,不是研发,生活和心态搞得不是很好
毕业后一直没有动力再去学习
所以劝各位在校生
本科一定要努力学好本专业知识,多参加竞赛,多拿奖!希望以后顺利吧。