Graph-Based Visual-Semantic Entanglement Network for Zero-Shot Image Recognition

相关资料

论文：Graph-Based Visual-Semantic Entanglement Network for Zero-Shot Image Recognition

摘要

零样本学习（Zero-shot learning, ZSL）使用语义属性来连接未见对象的搜索空间。近年来，尽管深度卷积网络为ZSL任务带来了强大的视觉建模能力，但其视觉特征存在严重的模式惯性和缺乏语义关系的表示，导致严重的偏差和歧义。为了解决这一问题，我们提出了一种基于知识图谱的视觉-语义纠缠网络（Graph-based Visual-Semantic Entanglement Network），通过知识图谱将视觉特征进行图建模，并映射到语义属性，该网络包含几个新颖设计：

1. 它建立了一个多路径纠缠网络，将卷积神经网络（CNN）和图卷积网络（GCN）相结合，将CNN的视觉特征输入到GCN中以模拟隐含的语义关系，然后GCN将图建模信息反馈到CNN特征；
2. 它使用属性词向量作为GCN图语义建模的目标，形成了图建模的自洽回归，以监督GCN学习更个性化的属性关系；
3. 它将通过图建模细化的层次化视觉-语义特征融合并补充到视觉嵌入中。

我们的方法在多个代表性的ZSL数据集上超越了现有的最先进方法：AwA2、CUB和SUN，通过促进视觉特征的语义链接建模。

引言

在ZSL任务中，输入图像表示为$x$。由CNN形成的视觉嵌入函数是$\theta (\cdot )$。与此分开的是，语义嵌入$\phi (y)$表示类别$y$的属性分布向量。$F(x,y,W_{\varphi })=F_{\varphi }(\theta (x),W_{\varphi })\phi (y)$是分类的得分函数。视觉嵌入和语义嵌入之间的唯一联系是视觉-语义桥接$F_{\varphi }(\cdot ,W_{\varphi })$，通常由几个全连接层（FC）构建。面对具有强烈模式惯性的视觉嵌入$\theta (\cdot )$，$F_{\varphi }(\cdot ,W_{\varphi })$承受着过度的建模压力，很难逆转预测偏差。尽管潜在属性机制减少了属性惯性引起的偏差，现有的ZSL模型仍然忽略了视觉特征中隐含的语义联系。
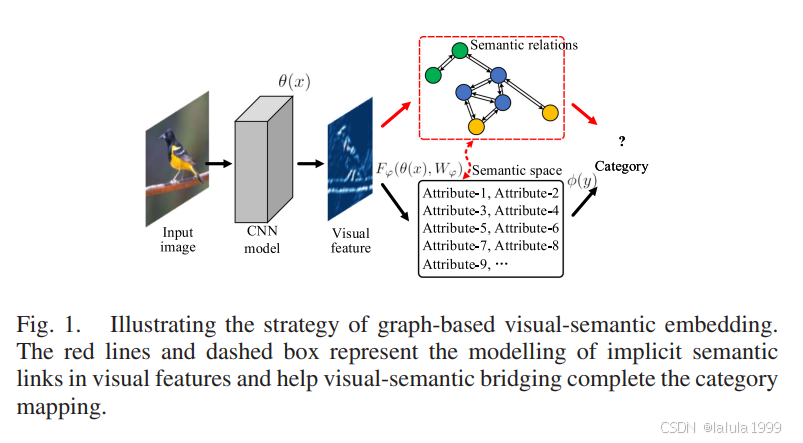
为了解决典型视觉特征缺乏属性内部关系知识的问题，我们必须利用属性连接的知识来补充映射、建模和融合隐含的语义关系，如图1中的红色部分所示。

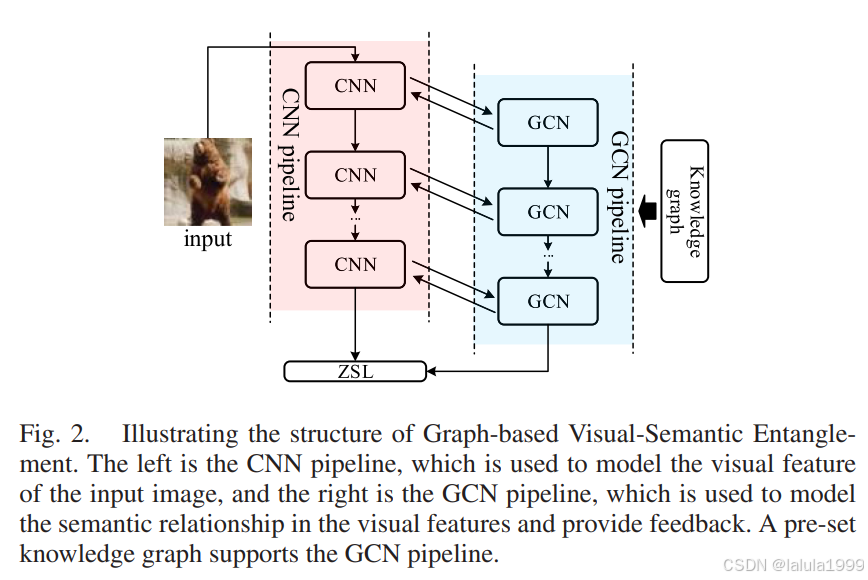
我们提出了基于知识图谱的视觉-语义纠缠（Graph-based Visual-Semantic Entanglement, GVSE）网络。如图2所示，GVSE网络主要提出了视觉-语义纠缠结构：我们假设应该有一种机制将属性空间中的概念映射到图像表示中的语义表示。
基于属性的图建模可以直接与视觉特征中的语义信息交互。为了利用在语义知识图谱中发现的属性之间的关系，我们构建了具有CNN和图卷积网络（GCN）两个纠缠管道的架构，我们将CNN视觉特征映射到基于属性的知识图谱，然后利用GCN对中间视觉特征的隐含语义关系进行建模，并向CNN提供反馈。GVSE网络还包括一些有效的设计：

1. 为了为模型提供更好的属性关系特征集，我们通过创建属性词向量来实现语义回归，创建了一个自洽的GCN建模系统。
2. 为了将这种新语义派生信息整合到经典的ZSL模型中，我们跳过了图建模的视觉特征到视觉嵌入$\theta (x)$的连接。目的是将图增强的特征融合到视觉嵌入中，并帮助从语义嵌入$\phi (y)$反向传播损失。

方法

问题公式化和符号说明

零样本学习(ZSL)的任务是这样设定的：
存在一个已知数据集$S=\{(x_i^s,y_i^s){\}}_{i=1}^{N^s}$，包含$N_s$个样本用于训练，其中$x_i^s$表示第$i$张图片，$y_i^s\in Y^S$是它的类别标签。
另有一个未见过的数据集$U=\{(x_i^u,y_i^u){\}}_{i=1}^{N^u}$，形式类似。
已知和未知的类别集合$Y^S$和$Y^U$遵循以下约束：$Y^S\cap Y^U=\varnothing ,Y^S\cup Y^U=Y$，其中$Y$是总类别集合。$Y^S$和$Y^U$共享一个语义属性空间：∀$y_i$ ∃ < Att1, …, Attm > 作为它们之间的唯一桥梁，且$y_i\in Y$。Atti指的是属性，通常是一个词或概念，$m$是属性的数量。
传统ZSL的目标是学习一个分类器，其搜索空间为未见过的类别$Y^U$。对于更具挑战性的广义ZSL(GZSL)，预期分类器的搜索空间是$Y$。

框架概述

为了实现ZSL的视觉-语义纠缠特征建模目标，必须采取以下步骤：

1. 构建语义知识图谱：为GCN的执行构建语义知识图谱。知识图谱提取属性的共现关系。

2. 建立视觉-语义双管道网络结构：如图2所示，建立清晰的职责分工的双管道网络结构，CNN负责传统的图像视觉建模，GCN负责视觉特征的语义关系图建模。

3. 设计CNN和GCN的纠缠策略：建立CNN视觉建模和GCN语义建模之间的交互功能。GCN接收CNN的视觉特征作为输入，CNN获取GCN的语义信息以进一步优化视觉特征。

4. 融合图语义编码和视觉表示：为了进一步加强ZSL桥接的先前特征表示，我们将GCN块中的语义图建模特征合并到最终视觉嵌入中。

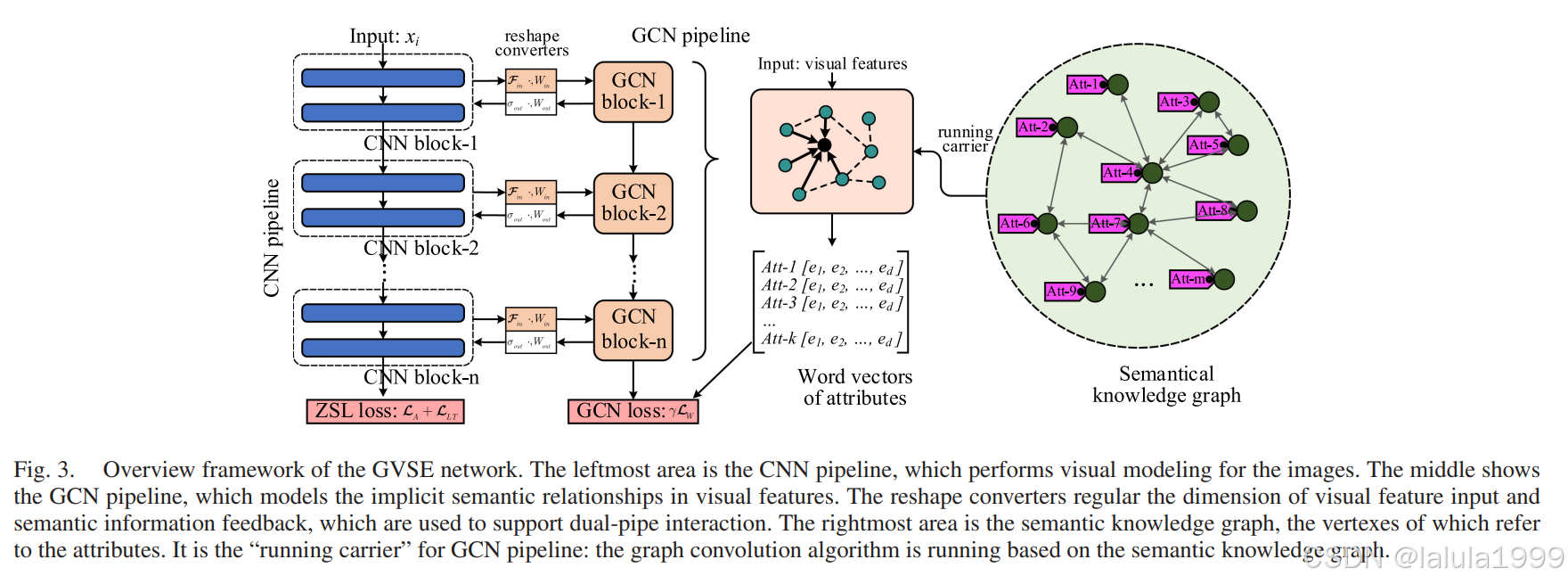
图3展示了GVSE网络的概述框架，它展示了属性的语义知识图谱，CNN视觉建模管道，GCN语义建模管道，双管道的目标输出，以及支持双管道纠缠的交互支持模块。

语义知识图谱

由于GCN需要在预定义的图结构上运行，因此在构建双管道视觉-语义神经网络架构之前，我们首先介绍语义知识图谱的构建策略。这个知识图谱将具有以下特征：

1. 视觉特征直接与属性映射。因此，知识图谱预期表示属性的基本关系；
2. 知识图谱的建立是离线的且方便；
3. 知识图谱的建立可以适用于各种场景，不受适应数据集的本体限制。

共现关系是属性之间基本联系之一。它可以通过统计属性在每个类别中共同出现的次数来获得。我们不使用WordNet作为先验知识图谱，而是基于所有类别的属性共现关系来构建语义知识图谱。具有共现关系的属性在相同类别的视觉表示中有很高概率存在。

知识图谱$G_{att}=(V,E)$包含顶点 V = { v 1 , v 2 , . . . , v m } V = \{v_1, v_2, ..., v_m\} V={v1​,v2​,...,vm​}和它们之间的边$E$。我们使用对称矩阵来编码边$[[l_{i,j}]]$，其中$l_{i,j}=1$表示顶点$v_i$和$v_j$之间存在链接，否则不是。我们的构建知识图谱需要属性空间表示明确的概念。在我们的语义知识图谱中，属性用于定义顶点，点互信息(PMI)[51]用于计算属性共现并确定属性顶点之间的连接，如下所示：

$\text{PMI}(v_i,v_j)=\frac{N}{\log p(v_i,v_j)-\log p(v_i)-\log p(v_j)}$

其中$\text{PMI}(v_i,v_j)$是属性$v_i$和$v_j$之间的PMI，$p(v)$是属性$v$的出现概率，共现概率$p(v_i,v_j)$是具有$v_i$和$v_j$的类别数量与总类别数量的比率。$N$表示在[0, 1]范围内的归一化函数。图3展示了我们语义知识图谱的构建策略，边是在PMI高于阈值$\delta$的顶点之间建立的，如下所示：

$l_{i,j}=\{\begin{array}{ll}1,& \text{if }\text{PMI}(v_i,v_j)>\delta \\ 0,& \text{otherwise}\end{array}$

双管道网络结构

我们设计的两个建模管道有明确的分工。我们首先定义CNN管道的视觉特征建模如下：

$\theta (x_i)=F_{conv}(x_i,W_{\theta })$

其中$x_i$指的是输入，$\theta (x_i)$是由CNN管道$F_{conv}$建模并提供的视觉嵌入，其参数由$W_{\theta }$指定。在我们的研究中，CNN管道$F_{conv}$可以由任何现有的流行CNN主干构成。

CNN管道的目标预测输出是ZSL分类分数$p(y|x_i)$，计算如下：

$p(y|x_i)=F_{\varphi }(\theta (x_i),W_{\varphi }{)}^T\varphi (y)$

其中$F_{\varphi }:{\mathbb{R}}^{d_v}\to {\mathbb{R}}^m$是属性预测层，参数为$W_{\varphi }\in {\mathbb{R}}^{d_v\times m}$，$\varphi (y)\in {\mathbb{R}}^{m\times |Y|}$表示类别$y$的属性分布。$d_v$是视觉特征的维度，$m$和$|Y|$分别指属性和类别的数量。

基于视觉特征中存在隐含的语义联系的前提，我们设计了GCN管道来对视觉特征中的语义关系进行建模。如图3所示，注意我们有来自CNN管道第$l$块的特征图$X^{(l)}=F_{conv}^{[,l]}(x_i,W_{\theta }^{[,l]})$，其中$[,l]$表示“从1到$l$”。我们使用$X^{(l)}$作为相应GCN块$F_G^{(l)}$的输入，如下所示：

$f_G^{(l)}=F_G^{(l)}(X^{(l)},<G_{att},W_G^{(l)}>)$

其中$f_G^{(l)}$是第$l$个GCN块的输出，$W_G^{(l)}$是运行在图$G_{att}$上的$F_G^{(l)}$的参数。符号$<\cdot ,\cdot >$必须一起使用。每个GCN块包含2层GCN，其定义在[17]中，如下所示：

$H^{(i+1)}=\sigma (D^{-1}{G}_a{H}^{(i)}{W}_G^{(i)})$

其中$H^{(i)}$和$H^{(i+1)}$分别表示GCN中的任意两层，$D$和$G_a$是预设知识图谱$G_{att}$的度矩阵和邻接矩阵，$W_G^{(i)}$表示第$i$层GCN的参数，$\sigma$是激活函数。在GCN管道中，我们为最初无序的视觉特征$X^{(l)}$赋予明确的属性定义，使得GCN：$F_G^{(l)}$根据图$G_{att}$描述的关系对它们进行建模，从而激活$X^{(l)}$中的隐含语义联系。

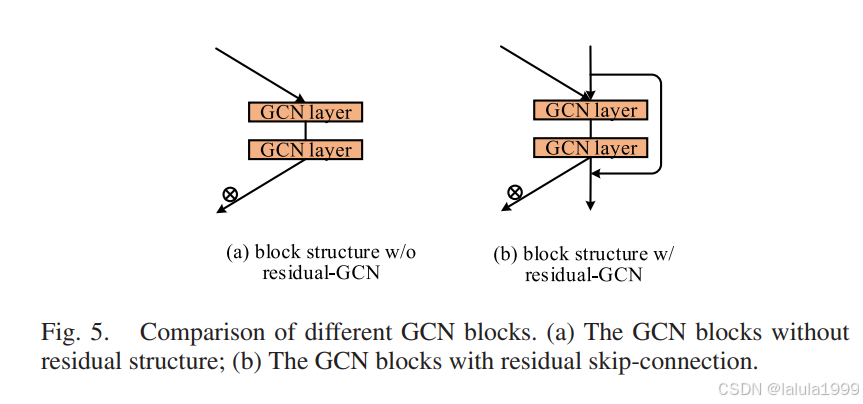
GCN管道将所有GCN块串联起来，为了解决GCN管道上的梯度扩散问题，我们采用了残差GCN结构，如图5(b)所示，如下所示：

$f_G^{(l+1)}=F_G^{(l+1)}(X^{(l+1)},f_G^{(l)},<G_{att},W_G^{(l+1)}>)+f_G^{(l)}$

由于我们记录GCN管道为$F_G$，其目标输出被设计为类别的属性词向量：

$A(x_i)=F_G(x_i,<G_{att},W_G>)$

其中$W_G$是GCN管道的参数，且

$A(x_i)=[a_1(x_i),a_2(x_i),...,a_k(x_i)]$

这是属性词向量的集合。$a_1(x_i)...a_k(x_i)$是属性$At{t}_1...At{t}_k$的词向量，这些属性属于真实类别$y_i$。

我们如何获得属性词向量

在ZSL数据集中，每个类别都有多个属性，这样我们可以将每个类别$y\in Y$视为属性集合{Att1, Att2, …, Attk}的集合，其中$k$是类别$y$具有的属性数量，然后我们可以将所有类别$Y$视为语料库。有了这个语料库，我们可以方便地使用现有的语言模型工具[22], [55]训练词嵌入$M_e$。像知识图谱$G_{att}$一样，词嵌入$M_e$的获取是离线且快速的。我们可以查询任意属性$At{t}_j$的词向量$a_j=[e_{1j},e_{2j},...,e_{dj}]\in {\mathbb{R}}^d$，其中$d$是词嵌入的固定维度。

我们之所以将GCN管道的目标输出设置为上述形式，是因为：

1. 作为一个基于词汇共现的模型，词向量可以与上述语义知识图谱$G_{att}$形成自洽的回归；
2. 语义知识图谱$G_{att}$仅提供了基于平均强属性共现的初始属性关系信息。GCN管道需要在词嵌入监督下学习更个性化的属性关系。

CNN和GCN的纠缠策略

仅构建CNN管道$F_{conv}$和GCN管道$F_G$是不够的。我们基于以下动机设计了它们之间的纠缠策略：

1. CNN和GCN管道的建模过程需要交互和同步；
2. 层次化的视觉特征需要接收有关语义关系建模的信息。本节详细介绍了从两个方向（CNN到GCN和GCN到CNN）的双管道纠缠策略。

对于CNN到GCN，我们已经描述了使用CNN块的特征图$X^{(l)}$作为GCN块的输入。然而，$X^{(l)}$的形状可能不适合GCN输入，因此我们需要首先重塑$X^{(l)}$，如下所示：

$X^{(l)}=F_{in}^{(l)}(X^{(l)},W_{in}^{(l)})$

此外，从第二个GCN块$F_G^{(2)}$开始，使用连接操作$\diamond$将特征图$X^{(l)}$和前一个GCN块的输出$f_G^{(l-1)}$合并作为输入。因此，我们可以更新方程5和7为：

$f_G^{(l)}=\{\begin{array}{ll}{F}_G^{(l)}(X^{(l)},<G_{att},W_G^{(l)}>),& \text{if }l=1\\ F_G^{(l)}(X^{(l)}\diamond F_{sq}(f_G^{(l-1)}),<G_{att},W_G^{(l)}>)+f_G^{(l-1)},& \text{if }l\ge 2\end{array}$

其中$F_{sq}$是压缩函数，它将$f_G^{(l-1)}$的维度降低到$d$以方便使用，它节省了$F_G^{(l)}$的计算。

对于GCN到CNN，我们应用门控机制将GCN管道的语义关系建模信息反馈到CNN管道的视觉特征中，如下所示：

${\tilde{X}}^{(l)}={\sigma }_{out}(f_G^{(l)},W_{out}^{(l)}\otimes X^{(l)})$

其中，权重$W_{out}^{(l)}$用于将图建模信息$f_G^{(l)}$的维度与特征图$X^{(l)}$对齐，其作用类似于$W_{in}^{(l)}$。${\sigma }_{out}$是激活函数，其输出值在[0, 1]范围内，操作$\otimes$是逐元素乘法，${\tilde{X}}^{(l)}$是新的视觉特征图，将继续输入到后续的CNN管道中，如下所示：$F_{conv}^{[l+1,)}({\tilde{X}}^{(l)},W_{\theta }^{[l+1,)})$，其中$[l+1,)$表示“从$l+1$到最后”。

所提出的GVSE网络的纠缠策略如图3所示，它使GVSE网络的双管道结构除了各自的精确建模功能外，还得到了充分的交互。我们的策略与基于注意力方法的其他ZSL模型[3], [16], [31], [56]有以下不同之处：1. 利用图建模优化视觉隐含语义信息；2. CNN的各层特征将获得优化和反馈。

GCN语义图建模在每个CNN层的动机是，我们认为各个CNN块的视觉特征包含隐含的语义关系信息，对每个CNN块的语义关系进行建模支持将视觉-语义建模整合到整个CNN管道中，从而为语义丰富的ZSL视觉嵌入提供完整的优化。换句话说，我们的语义图建模视觉特征不会被压缩到一个块中。它将均匀分布在层次结构中，共享语义建模压力并获取层次化的视觉-语义信息。

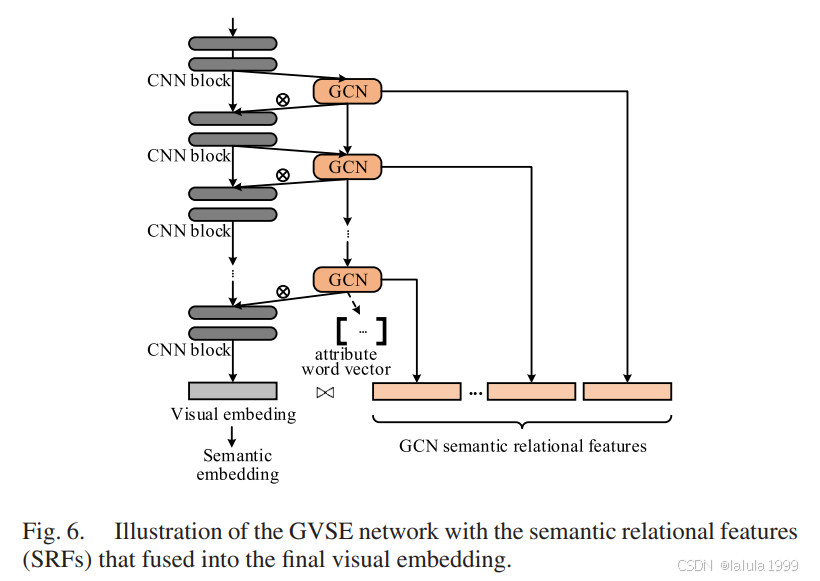
将层次化语义特征整合到视觉嵌入中

为了进一步加强最终的视觉嵌入，我们执行了最后一步。如图6所示，受金字塔结构[57]的启发，我们将来自GCN管道的语义特征合并到最终视觉嵌入$\theta (x)$中，即语义关系特征(SRF)。它的优点是：1. 帮助损失函数反向传播到GCN块；2. 为潜在属性[9], [16]提供更多语义信息。

注意，最终的视觉嵌入是通过全局平均池化集中的：

$\theta (x_i)=\frac{1}{R\times C}{\sum }_{r=1}^R{\sum }_{c=1}^C{F}_{conv}^{[]}(x_i,W_{\theta })[r,c]$

其中$F_{conv}^{[]}$是CNN管道全局池化前的F部分，(R × C)是CNN管道最终特征图的形状，$F_{conv}^{[]}(x_i,W_{\theta })[r,c]$表示CNN特征图上第$r$行第$c$列的信号。

整合的视觉嵌入$\theta (x{)}^{+}$如下所示：

$\theta (x{)}^{+}=\theta (x)\diamond {\hat{f}}_G^{(1)}\diamond {\hat{f}}_G^{(2)}\diamond ...\diamond {\hat{f}}_G^{(L)}$

其中

${\hat{f}}_G^{(i)}=\frac{1}{k}{\sum }_{v=1}^k{F}_{sq}(f_G^{(i)}[v])$

这是用于汇聚GCN输出的属性词向量，$k$是属性数量。$F_{sq}$是一个压缩函数，用于减少GCN输出的宽度。

优化细节和ZSL预测

本研究中的GVSE网络为ZSL提供了更强大的语义关系表示特征，这适用于各种ZSL框架。由于我们在第三节中介绍了GVSE网络的双管道前馈特征建模方法，在这一部分中，我们简要描述了使用GVSE网络进行ZSL预测的方法和GVSE特征的优化方法。

我们从归纳和演绎这两种ZSL设置中引入了ZSL预测和优化的执行。所提出的GVSE网络使用反向传播(BP)算法[58]进行优化，损失函数指示了详细的优化策略。

A. 归纳ZSL设置

由于方程4制定了ZSL预测的分数函数，我们选择具有最大分数的标签作为：

$y_i^{\ast }=\arg {\max }_{y\in Y}p(y|x_i)=\arg {\max }_{y\in Y}\varphi (x_i{)}^T\varphi (y)$

其中$\varphi (x_i)=F_{\varphi }(\theta (x_i{)}^{+},W_{\varphi })$指的是目标属性的视觉-语义投影。

我们还引入了潜在属性(LA)[9], [16]来补充人工定义的属性空间的不完美。这种机制需要计算所有类别的潜在属性原型，对于已知类别：${\varphi }_{lat}(y_s)=\frac{1}{N}\sum {\varphi }_{lat}(x_i)$，其中${\varphi }_{lat}(x_i)$表示特定于潜在属性的区分特征，由[9]详细说明。对于未知类别，原型可以从岭回归中获得：

${\beta }_{u_y}=\arg {\min }_{y\in Y_S}\Vert \varphi (y_u)-{\sum }_{y\in Y_S}{\beta }_{u_y}\varphi (y){\Vert }_2^2+\Vert {\beta }_{u_y}{\Vert }_2^2$

${\varphi }_{lat}(y_u)={\sum }_{y\in Y_S}{\beta }_{u_y}{\varphi }_{lat}(y)$

然后，ZSL预测执行如下：

$y_i^{\ast }=\arg {\max }_{y\in Y}(\varphi (x_i{)}^T\varphi (y)+{\varphi }_{lat}(x_i{)}^T{\varphi }_{lat}(y))$

由于我们有了上述ZSL预测过程，损失函数设置如下，我们使用softmax交叉熵损失来优化视觉-语义桥接，如下所示：

$L_A=-\frac{1}{N}{\sum }_{i=1}^N\log \frac{e^{\varphi (x_i{)}^T\varphi (y_i)}}{{\sum }_{y\in Y_S}{e}^{\varphi (x_i{)}^T\varphi (y)}}$

对于区分特征${\varphi }_{lat}$，我们遵循[9], [16]中的相同策略，使用三元组损失[62]来扩大类间距离并减少类内距离：

$L_{LT}=\frac{1}{N}{\sum }_{i=1}^N[\Vert {\varphi }_{lat}(x_i)-{\varphi }_{lat}(x_j){\Vert }^2-\Vert {\varphi }_{lat}(x_i)-{\varphi }_{lat}(x_r){\Vert }^2+\alpha {]}_{+}$

其中$x_i,x_j,$和$x_r$分别代表三元组中的锚点、正样本和负样本，$[\cdot {]}_{+}$等同于$\max (0,\cdot )$，$\alpha$是三元组损失的边界，在所有实验中为1.0。

由于方程8中我们使用属性词向量作为GCN管道$F_G$的目标输出，均方误差被用作该分支的损失，如下所示：

$L_W=\frac{1}{N}{\sum }_{i=1}^N{\sum }_{v=1}^{k_i}{\left(F_{sq}(f_G^{(L)}(x_i)[v])-a_v(y_i)\right)}^2$

其中$f_G^{(L)}$表示来自最后一个GCN块的输出特征，$k_i$是属于类别$y_i$的属性数量。

完整的损失函数如下：

$L=L_A+L_{LT}+\gamma L_W$

B. 演绎ZSL设置

我们也将在GVSE网络中学习到的关系增强特征应用于三个演绎ZSL框架：1. 准全监督学习(QFSL)[7]；2. 自适应(SA)[16]；3. 基于Wasserstein距离的视觉结构约束(WDVSc)[15]。这些演绎ZSL方法都向模型开放对未见过数据的访问，从而缓解了“领域偏移”现象。

其中，SA方法需要与LA机制[9]一起执行；它吸收了未见过类别的信息，并进行了几次离线迭代，以更新原型${\varphi }_{lat}(y_u)$和未见过类别的属性分布$\varphi (y_u)$。

另外两种演绎ZSL方法没有与LA机制一起使用。在QFSL中，在损失函数中增加了一个偏置项$L_B=\frac{1}{N_u}{\sum }_{i=1}^{N_u}(-\log ({\sum }_{y\in Y_U}p(y|x_i)))$，以鼓励模型输出未见过类别的分类结果。

在WDVSc中，使用Wasserstein距离[63]来校正语义演绎空间中未见类别的聚类中心的位置。它通过计算特征分布与类别聚类中心之间的距离来确定分类结果。

这些演绎ZSL方法中的特殊设计预测和优化不会影响GVSE网络对关系增强视觉嵌入$\theta (x{)}^{+}$的建模。它们的详细实现在原始研究[7], [15], [16]中有描述。

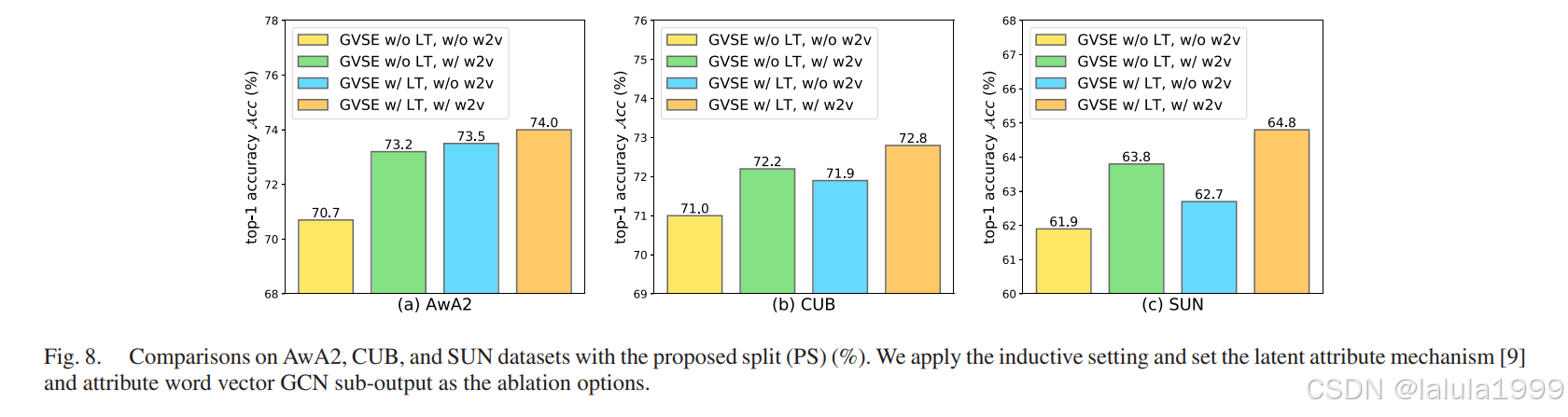
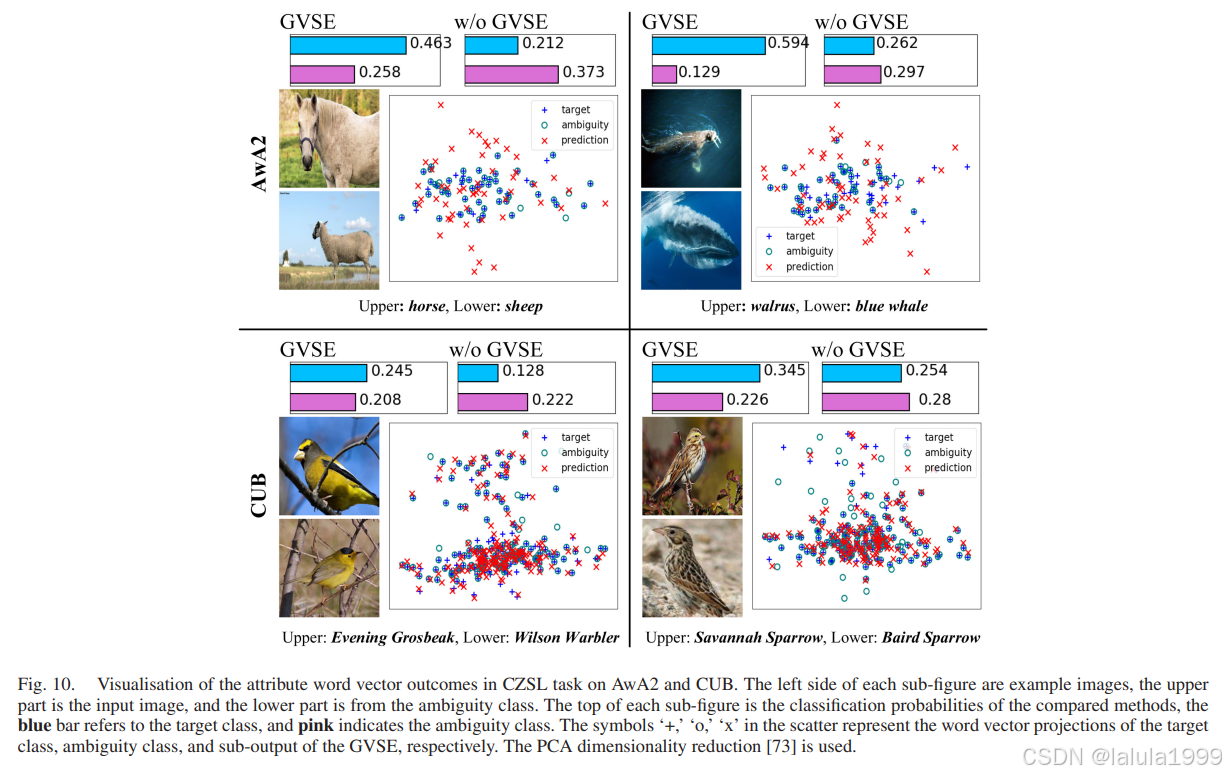
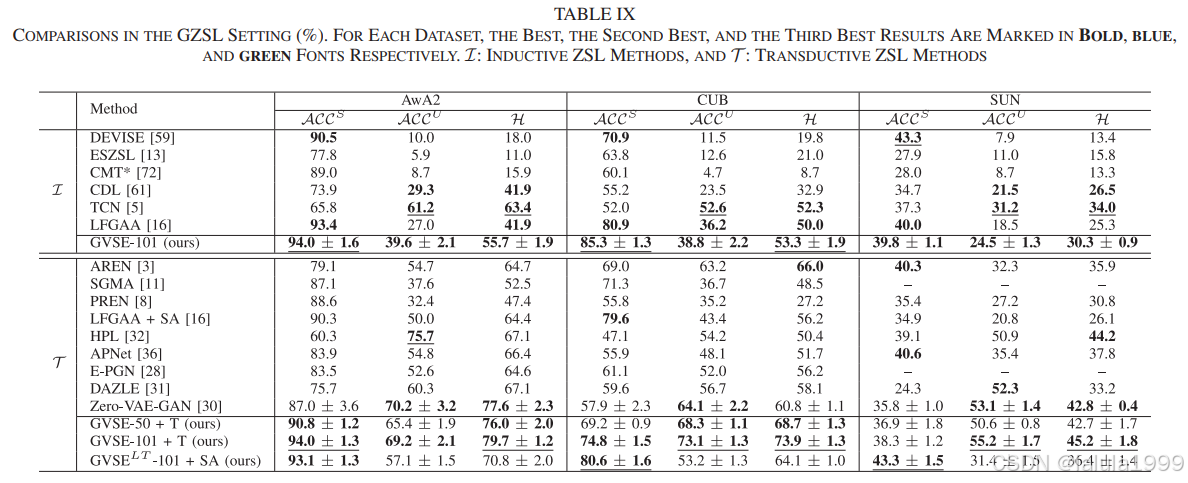
实验