支持向量机SVM——最大间隔分离超平面的计算
如何定义两个集合的最优分隔超平面呢?
找到集合"边界"上的若干点,以这些点为基础计算超平面的方向,以二维坐标平面为例子 w T x + b = 0 w^Tx+b=0 wTx+b=0,当系数 w T w^T wT确定的时候,这个超平面的方向也就随之确定,以两个结果边界上的点的平均作为超平面的"截距"。
SVM线性分类问题
-
假设给定一个特征空间上的训练数据集 T = ( x 1 , t 1 ) , ( x 2 , t 2 ) . . . ( x N , t N ) T={(x_1,t_1),(x_2,t_2)...(x_N,t_N)} T=(x1,t1),(x2,t2)...(xN,tN),其中, x i ∈ R n , t i ∈ { + 1 , − 1 } , i = 1 , 2.... N x_i\in R^n,t_i\in\{+1,-1\},i=1,2....N xi∈Rn,ti∈{+1,−1},i=1,2....N
-
x i x_i xi为第 i i i个实例(若 n > 1 n>1 n>1, x i x_i xi为向量)
-
t i t_i ti为 x i x_i xi类的标记,当 t i = + 1 t_i=+1 ti=+1时,成 x i x_i xi为正例;当 t i = − 1 t_i=-1 ti=−1时,称 x i x_i xi为负例, ( x i , t i ) (x_i,t_i) (xi,ti)为样本点。
给定一个线性可分训练数据集,通过间隔最大化得到的最优分隔超平面为 y ( x ) = w T φ ( x ) + b y(x)=w^Tφ(x)+b y(x)=wTφ(x)+b,相应的分类决策函数为 f ( x ) = s i g n ( w T φ ( x ) + b ) f(x)=sign(w^Tφ(x)+b) f(x)=sign(wTφ(x)+b)
这里为什么说是 w T φ ( x ) w^Tφ (x) wTφ(x)而不是 w T x w^Tx wTx呢?这是因为有些时候是线性不可分的,但是在低维度线性不可分的通过一定的函数作用映射到更高维的空间的时候就可能可分。
举个栗子:空间中有两个球,在灯光的照射下投影到一个平面上,这两个球的投影是相交的,不可分的,但是在空间中是线性可分的,完全可以找到一个平面将两个球分割开来,即使这两个球是紧挨的,但是还是可以找到与这两个球相切的这样一个超平面将两个球分隔开来。
将上述问题整理得到
- 分割平面 y ( x ) = w T φ ( x ) + b y(x)=w^Tφ(x)+b y(x)=wTφ(x)+b
- 训练集 X 1 , X 2 , . . . X N X_1,X_2,...X_N X1,X2,...XN
- 目标值 t 1 , t 2 , . . . t N t_1,t_2,...t_N t1,t2,...tN
- 新数据的分类: s i g n ( y ( x ) ) sign(y(x)) sign(y(x))
线性可分支持向量机
推导目标函数,根据给定的条件, y ( x n ) > 0 y(x_n)>0 y(xn)>0时候, y i = + 1 y_i=+1 yi=+1;当 y ( x n ) < 0 y(x_n)<0 y(xn)<0时候, y i = − 1 y_i = -1 yi=−1
假设存在超平面 ( w ′ ) ⊤ x + b ′ = 0 \left(\boldsymbol{w}^{\prime}\right)^{\top} \boldsymbol{x}+b^{\prime}=0 (w′)⊤x+b′=0,对于 ( x i , y i ) ∈ D \left(\boldsymbol{x}_{i}, y_{i}\right) \in D (xi,yi)∈D,有 { ( w ′ ) ⊤ x i + b ′ > 0 , y i = + 1 ( w ′ ) ⊤ x i + b ′ < 0 , y i = − 1 \left\{\begin{array}{ll}{\left(\boldsymbol{w}^{\prime}\right)^{\top} \boldsymbol{x}_{i}+b^{\prime}>0,} & {y_{i}=+1} \\ {\left(\boldsymbol{w}^{\prime}\right)^{\top} \boldsymbol{x}_{i}+b^{\prime}<0,} & {y_{i}=-1}\end{array}\right. {(w′)⊤xi+b′>0,(w′)⊤xi+b′<0,yi=+1yi=−1
根据几何间隔,将以上关系修正为:
{
(
w
′
)
⊤
x
i
+
b
′
≥
+
ζ
,
y
i
=
+
1
(
w
′
)
⊤
x
i
+
b
′
≤
−
ζ
,
y
i
=
−
1
\left\{\begin{array}{ll}{\left(\boldsymbol{w}^{\prime}\right)^{\top} \boldsymbol{x}_{i}+b^{\prime} \geq+\zeta,} & {y_{i}=+1} \\ {\left(\boldsymbol{w}^{\prime}\right)^{\top} \boldsymbol{x}_{i}+b^{\prime} \leq-\zeta,} & {y_{i}=-1}\end{array}\right.
{(w′)⊤xi+b′≥+ζ,(w′)⊤xi+b′≤−ζ,yi=+1yi=−1
其中
ζ
\zeta
ζ为某个大于零的常数,两边同除以
ζ
\zeta
ζ,再次修正以上关系为:
{
(
1
ζ
w
′
)
⊤
x
i
+
b
′
ζ
≥
+
1
,
y
i
=
+
1
(
1
ζ
w
′
)
⊤
x
i
+
b
′
ζ
≤
−
1
,
y
i
=
−
1
\left\{\begin{array}{ll}{\left(\frac{1}{\zeta} \boldsymbol{w}^{\prime}\right)^{\top} \boldsymbol{x}_{i}+\frac{b^{\prime}}{\zeta} \geq+1,} & {y_{i}=+1} \\ {\left(\frac{1}{\zeta} \boldsymbol{w}^{\prime}\right)^{\top} \boldsymbol{x}_{i}+\frac{b^{\prime}}{\zeta} \leq-1,} & {y_{i}=-1}\end{array}\right.
⎩⎪⎨⎪⎧(ζ1w′)⊤xi+ζb′≥+1,(ζ1w′)⊤xi+ζb′≤−1,yi=+1yi=−1
令:
w
=
1
ζ
w
′
,
b
=
b
′
ζ
\boldsymbol{w}=\frac{1}{\zeta} \boldsymbol{w}^{\prime}, b=\frac{b^{\prime}}{\zeta}
w=ζ1w′,b=ζb′,则以上关系可写为:
{
w
⊤
x
i
+
b
≥
+
1
,
y
i
=
+
1
w
⊤
x
i
+
b
≤
−
1
,
y
i
=
−
1
\left\{\begin{array}{ll}{\boldsymbol{w}^{\top} \boldsymbol{x}_{i}+b \geq+1,} & {y_{i}=+1} \\ {\boldsymbol{w}^{\top} \boldsymbol{x}_{i}+b \leq-1,} & {y_{i}=-1}\end{array}\right.
{w⊤xi+b≥+1,w⊤xi+b≤−1,yi=+1yi=−1
将上述公式进行整合,可得
y
i
(
w
T
x
i
+
b
)
≥
1
y_i(w^Tx_i+b)\ge1
yi(wTxi+b)≥1
举个栗子:以二维平面为例子
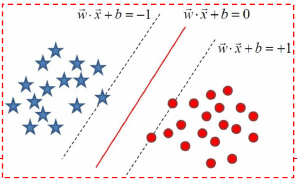
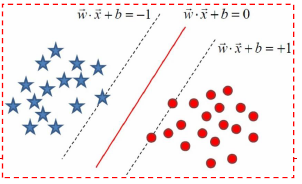
如上图,在上图中使用SVM实现线性可分就是找到各类样本点距离分隔超平面的距离最大,也就是找到最大间隔分离超平面。这个超平面用
w
T
x
+
b
=
0
w^Tx+b=0
wTx+b=0表示(实际上任意超平面都可以用该公式表示)。在二维平面中,点
(
x
,
y
)
(x,y)
(x,y)到超平面
A
x
+
B
y
+
C
=
0
Ax+By+C=0
Ax+By+C=0的距离为
∣
A
x
+
B
y
+
C
∣
A
2
+
B
2
\begin{aligned}\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}\end{aligned}
A2+B2∣Ax+By+C∣
扩展到 n n n维度空间中点 x = ( x 1 , x 2 , x 3 . . . x n ) x = (x_1,x_2,x_3...x_n) x=(x1,x2,x3...xn)到超平面的距离为 ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ 2 \begin{aligned}\frac{|w^Tx+b|}{||w||_2}\end{aligned} ∣∣w∣∣2∣wTx+b∣
向量 w w w的二范数 ∣ ∣ w ∣ ∣ 2 = x 1 2 + x 2 2 + . . . + x n 2 ||w||_2=\sqrt{x_1^2+x_2^2+...+x_n^2} ∣∣w∣∣2=x12+x22+...+xn2
但是这里的 ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ 2 \begin{aligned}\frac{|w^Tx+b|}{||w||_2}\end{aligned} ∣∣w∣∣2∣wTx+b∣应该是 ∣ w T φ ( x ) + b ∣ ∣ ∣ w ∣ ∣ 2 \begin{aligned}\frac{|w^Tφ(x)+b|}{||w||_2}\end{aligned} ∣∣w∣∣2∣wTφ(x)+b∣,因为原公式中的 x x x有可能是经过某种函数映射得到高维空间中得到的,而不是原始的 x x x, φ ( x ) φ(x) φ(x)的最简单的形式就是未经处理的 x x x。
于是得到这样的公式 y i ( w T φ ( x n ) + b ) ∣ ∣ w ∣ ∣ 2 ≥ d \begin{aligned}\frac{y_i(w^Tφ(x_n)+b)}{||w||_2}\ge d\end{aligned} ∣∣w∣∣2yi(wTφ(xn)+b)≥d
那么
y
i
(
w
T
φ
(
x
n
)
+
b
)
∣
∣
w
∣
∣
2
d
≥
1
\begin{aligned}\frac{y_i(w^Tφ(x_n)+b)}{||w||_2d}\ge 1\end{aligned}
∣∣w∣∣2dyi(wTφ(xn)+b)≥1
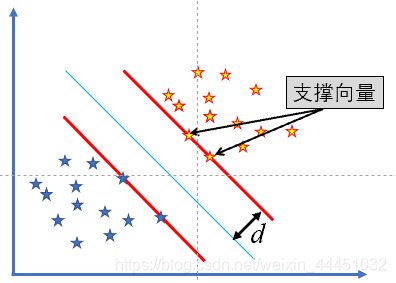
每个支撑向量到超平面的距离为 d = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ 2 d = \begin{aligned}\frac{|w^Tx+b|}{||w||_2}\end{aligned} d=∣∣w∣∣2∣wTx+b∣
我们的目标是求出最大间隔分离超平面,所以最大化这个距离
因为是两边,所以对每边的支撑向量到超平面的距离最大化 m a x 2 ∗ ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ 2 max2*\begin{aligned}\frac{|w^Tx+b|}{||w||_2}\end{aligned} max2∗∣∣w∣∣2∣wTx+b∣
在给定样本后 ∣ w T x + b ∣ |w^Tx+b| ∣wTx+b∣的值是常数,那么这个最大化距离就变成了求 m i n 1 2 ∣ ∣ w ∣ ∣ 2 \begin{aligned}min\frac{1}{2}||w||_2\end{aligned} min21∣∣w∣∣2
为了求导和计算方便我们求的就是 m i n 1 2 ∣ ∣ w ∣ ∣ 2 2 \begin{aligned}min\frac{1}{2}||w||_2^2\end{aligned} min21∣∣w∣∣22
所以我们最终的问题就转化成了求 m i n 1 2 ∣ ∣ w ∣ ∣ 2 2 , s t , y i ( w T x i + b ) ≥ 1 \begin{aligned}min\frac{1}{2}||w||_2^2,\quad st,\quad \begin{aligned}y_i(w^Tx_i+b)\ge1\end{aligned}\end{aligned} min21∣∣w∣∣22,st,yi(wTxi+b)≥1
这不就是不等式约束优化问题吗?——拉格朗日乘数法请查看我的另外的博文拉格朗日乘数法
拉格朗日乘数法求解不等式约束的优化问题
不等式约束就转化为等式约束问题求解, y i ( w T x i + b ) ≥ 1 \begin{aligned}y_i(w^Tx_i+b)\ge1\end{aligned} yi(wTxi+b)≥1,那么
− y i ( w T x i + b ) ≤ − 1 \begin{aligned}-y_i(w^Tx_i+b)\le-1\end{aligned} −yi(wTxi+b)≤−1
进而得到 − y i ( w T x i + b ) + 1 ≤ 0 \begin{aligned}-y_i(w^Tx_i+b)+1\le0 \end{aligned} −yi(wTxi+b)+1≤0
那么利用拉格朗日乘数法构造函数
L
(
w
,
b
,
α
)
=
1
2
∥
w
∥
2
+
∑
i
=
1
m
α
i
(
1
−
y
i
(
w
⊤
x
i
+
b
)
)
L(\boldsymbol{w}, b, \boldsymbol{\alpha})=\frac{1}{2}\|\boldsymbol{w}\|^{2}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{x}_{i}+b\right)\right)
L(w,b,α)=21∥w∥2+i=1∑mαi(1−yi(w⊤xi+b))
原问题求
m
i
n
1
2
∣
∣
w
∣
∣
2
\begin{aligned}min\frac{1}{2}||w||_2\end{aligned}
min21∣∣w∣∣2,转化为求
min
w
,
b
max
α
L
(
w
,
b
,
α
)
\begin{aligned}\min_{\boldsymbol{w},b}\max_{\boldsymbol{\alpha}}L(\boldsymbol{w},b,\boldsymbol{\alpha}) \end{aligned}
w,bminαmaxL(w,b,α)
L
(
w
,
b
,
α
)
=
1
2
∣
∣
w
∣
∣
2
+
∑
i
=
1
m
α
i
(
1
−
y
i
(
w
T
x
i
+
b
)
)
=
1
2
∣
∣
w
∣
∣
2
+
∑
i
=
1
m
(
α
i
−
α
i
y
i
w
T
x
i
−
α
i
y
i
b
)
=
1
2
w
T
w
+
∑
i
=
1
m
α
i
−
∑
i
=
1
m
α
i
y
i
w
T
x
i
−
∑
i
=
1
m
α
i
y
i
b
\begin{aligned} L(\boldsymbol{w},b,\boldsymbol{\alpha}) &= \frac{1}{2}||\boldsymbol{w}||^2+\sum_{i=1}^m\alpha_i(1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)) \\ & = \frac{1}{2}||\boldsymbol{w}||^2+\sum_{i=1}^m(\alpha_i-\alpha_iy_i \boldsymbol{w}^T\boldsymbol{x}_i-\alpha_iy_ib)\\ & =\frac{1}{2}\boldsymbol{w}^T\boldsymbol{w}+\sum_{i=1}^m\alpha_i -\sum_{i=1}^m\alpha_iy_i\boldsymbol{w}^T\boldsymbol{x}_i-\sum_{i=1}^m\alpha_iy_ib \end{aligned}
L(w,b,α)=21∣∣w∣∣2+i=1∑mαi(1−yi(wTxi+b))=21∣∣w∣∣2+i=1∑m(αi−αiyiwTxi−αiyib)=21wTw+i=1∑mαi−i=1∑mαiyiwTxi−i=1∑mαiyib
对
w
\boldsymbol{w}
w和
b
b
b分别求偏导数并令其等于0:
∂ L ∂ w = 1 2 × 2 × w + 0 − ∑ i = 1 m α i y i x i − 0 = 0 ⟹ w = ∑ i = 1 m α i y i x i \frac {\partial L}{\partial \boldsymbol{w}}=\frac{1}{2}\times2\times\boldsymbol{w} + 0 - \sum_{i=1}^{m}\alpha_iy_i \boldsymbol{x}_i-0= 0 \Longrightarrow \boldsymbol{w}=\sum_{i=1}^{m}\alpha_iy_i \boldsymbol{x}_i ∂w∂L=21×2×w+0−i=1∑mαiyixi−0=0⟹w=i=1∑mαiyixi
∂ L ∂ b = 0 + 0 − 0 − ∑ i = 1 m α i y i = 0 ⟹ ∑ i = 1 m α i y i = 0 \frac {\partial L}{\partial b}=0+0-0-\sum_{i=1}^{m}\alpha_iy_i=0 \Longrightarrow \sum_{i=1}^{m}\alpha_iy_i=0 ∂b∂L=0+0−0−i=1∑mαiyi=0⟹i=1∑mαiyi=0
所以得到
w = ∑ i = 1 m α i y i x i 0 = ∑ i = 1 m α i y i \begin{aligned} w &= \sum_{i=1}^m\alpha_iy_i\boldsymbol{x}_i \\ 0 &=\sum_{i=1}^m\alpha_iy_i \end{aligned} w0=i=1∑mαiyixi=i=1∑mαiyi
代入 L ( w , b , α ) = 1 2 ∥ w ∥ 2 + ∑ i = 1 m α i ( 1 − y i ( w ⊤ x i + b ) ) L(\boldsymbol{w}, b, \boldsymbol{\alpha})=\frac{1}{2}\|\boldsymbol{w}\|^{2}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{x}_{i}+b\right)\right) L(w,b,α)=21∥w∥2+i=1∑mαi(1−yi(w⊤xi+b))得到
min
w
,
b
L
(
w
,
b
,
α
)
=
1
2
w
T
w
+
∑
i
=
1
m
α
i
−
∑
i
=
1
m
α
i
y
i
w
T
x
i
−
∑
i
=
1
m
α
i
y
i
b
=
1
2
w
T
∑
i
=
1
m
α
i
y
i
x
i
−
w
T
∑
i
=
1
m
α
i
y
i
x
i
+
∑
i
=
1
m
α
i
−
b
∑
i
=
1
m
α
i
y
i
=
−
1
2
w
T
∑
i
=
1
m
α
i
y
i
x
i
+
∑
i
=
1
m
α
i
−
b
∑
i
=
1
m
α
i
y
i
\begin{aligned} \min_{\boldsymbol{w},b} L(\boldsymbol{w},b,\boldsymbol{\alpha}) &=\frac{1}{2}\boldsymbol{w}^T\boldsymbol{w}+\sum_{i=1}^m\alpha_i -\sum_{i=1}^m\alpha_iy_i\boldsymbol{w}^T\boldsymbol{x}_i-\sum_{i=1}^m\alpha_iy_ib \\ &=\frac {1}{2}\boldsymbol{w}^T\sum _{i=1}^m\alpha_iy_i\boldsymbol{x}_i-\boldsymbol{w}^T\sum _{i=1}^m\alpha_iy_i\boldsymbol{x}_i+\sum _{i=1}^m\alpha_ i -b\sum _{i=1}^m\alpha_iy_i \\ & = -\frac {1}{2}\boldsymbol{w}^T\sum _{i=1}^m\alpha_iy_i\boldsymbol{x}_i+\sum _{i=1}^m\alpha_i -b\sum _{i=1}^m\alpha_iy_i \end{aligned}
w,bminL(w,b,α)=21wTw+i=1∑mαi−i=1∑mαiyiwTxi−i=1∑mαiyib=21wTi=1∑mαiyixi−wTi=1∑mαiyixi+i=1∑mαi−bi=1∑mαiyi=−21wTi=1∑mαiyixi+i=1∑mαi−bi=1∑mαiyi
又
∑
i
=
1
m
α
i
y
i
=
0
\sum\limits_{i=1}^{m}\alpha_iy_i=0
i=1∑mαiyi=0,所以上式最后一项可化为0,于是得:
min
w
,
b
L
(
w
,
b
,
α
)
=
−
1
2
w
T
∑
i
=
1
m
α
i
y
i
x
i
+
∑
i
=
1
m
α
i
=
−
1
2
(
∑
i
=
1
m
α
i
y
i
x
i
)
T
(
∑
i
=
1
m
α
i
y
i
x
i
)
+
∑
i
=
1
m
α
i
=
−
1
2
∑
i
=
1
m
α
i
y
i
x
i
T
∑
i
=
1
m
α
i
y
i
x
i
+
∑
i
=
1
m
α
i
=
∑
i
=
1
m
α
i
−
1
2
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
x
i
T
x
j
\begin{aligned} \min_{\boldsymbol{w},b} L(\boldsymbol{w},b,\boldsymbol{\alpha}) &= -\frac {1}{2}\boldsymbol{w}^T\sum _{i=1}^m\alpha_iy_i\boldsymbol{x}_i+\sum _{i=1}^m\alpha_i \\ &=-\frac {1}{2}(\sum_{i=1}^{m}\alpha_iy_i\boldsymbol{x}_i)^T(\sum _{i=1}^m\alpha_iy_i\boldsymbol{x}_i)+\sum _{i=1}^m\alpha_i \\ &=-\frac {1}{2}\sum_{i=1}^{m}\alpha_iy_i\boldsymbol{x}_i^T\sum _{i=1}^m\alpha_iy_i\boldsymbol{x}_i+\sum _{i=1}^m\alpha_i \\ &=\sum _{i=1}^m\alpha_i-\frac {1}{2}\sum_{i=1 }^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j \end{aligned}
w,bminL(w,b,α)=−21wTi=1∑mαiyixi+i=1∑mαi=−21(i=1∑mαiyixi)T(i=1∑mαiyixi)+i=1∑mαi=−21i=1∑mαiyixiTi=1∑mαiyixi+i=1∑mαi=i=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj
所以根据强对偶性就转化为求 α \alpha α,使得 0 = ∑ i = 1 m α i y i \begin{aligned}0 =\sum_{i=1}^m\alpha_iy_i\end{aligned} 0=i=1∑mαiyi
max α min w , b L ( w , b , α ) = max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j \begin{aligned}\max_{\boldsymbol{\alpha}}\min_{\boldsymbol{w},b} L(\boldsymbol{w},b,\boldsymbol{\alpha}) =\max_{\boldsymbol{\alpha}} \sum_{i=1}^m\alpha_i - \frac{1}{2}\sum_{i = 1}^m\sum_{j=1}^m\alpha_i \alpha_j y_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j \end{aligned} αmaxw,bminL(w,b,α)=αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj
求出 α \alpha α之后代入 w ∗ = ∑ i = 1 m α i y i x i \begin{aligned}w^* = \sum_{i=1}^m\alpha_iy_i\boldsymbol{x}_i\end{aligned} w∗=i=1∑mαiyixi即可解得 w w w,然后 b ∗ = y i − w ∗ x j = ∑ i = 1 m α i y i x i x j b^* = y_i-\begin{aligned}w^*x_j = \sum_{i=1}^m\alpha_iy_i\boldsymbol{x}_i\boldsymbol{x}_j\end{aligned} b∗=yi−w∗xj=i=1∑mαiyixixj
然后求得分离超平面 w ∗ T x + b = 0 {w^*}^Tx+b=0 w∗Tx+b=0
那么分类决策函数就是 f ( x ) = s i g n ( w ∗ T x + b ) \begin{aligned}f(x)=sign({w^*}^Tx+b)\end{aligned} f(x)=sign(w∗Tx+b)