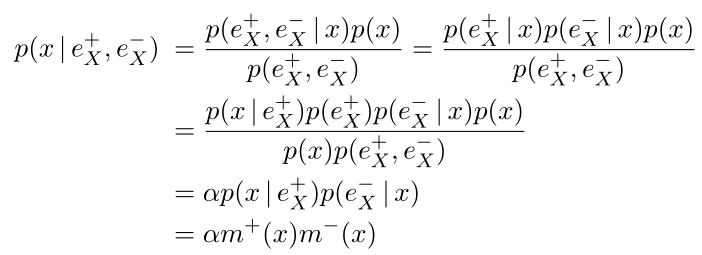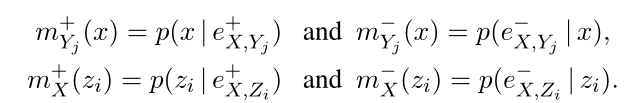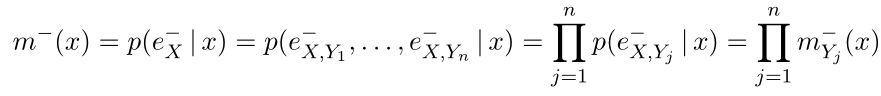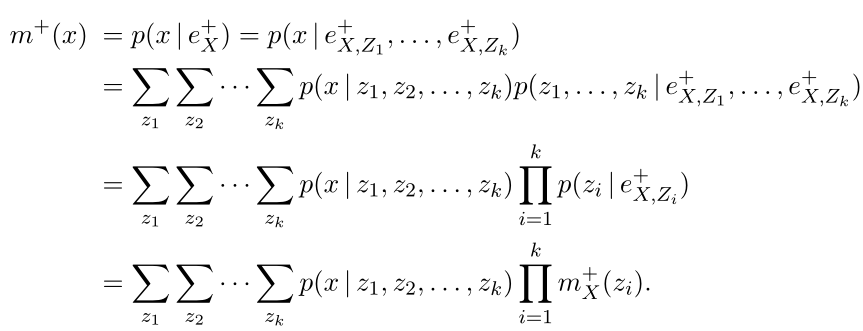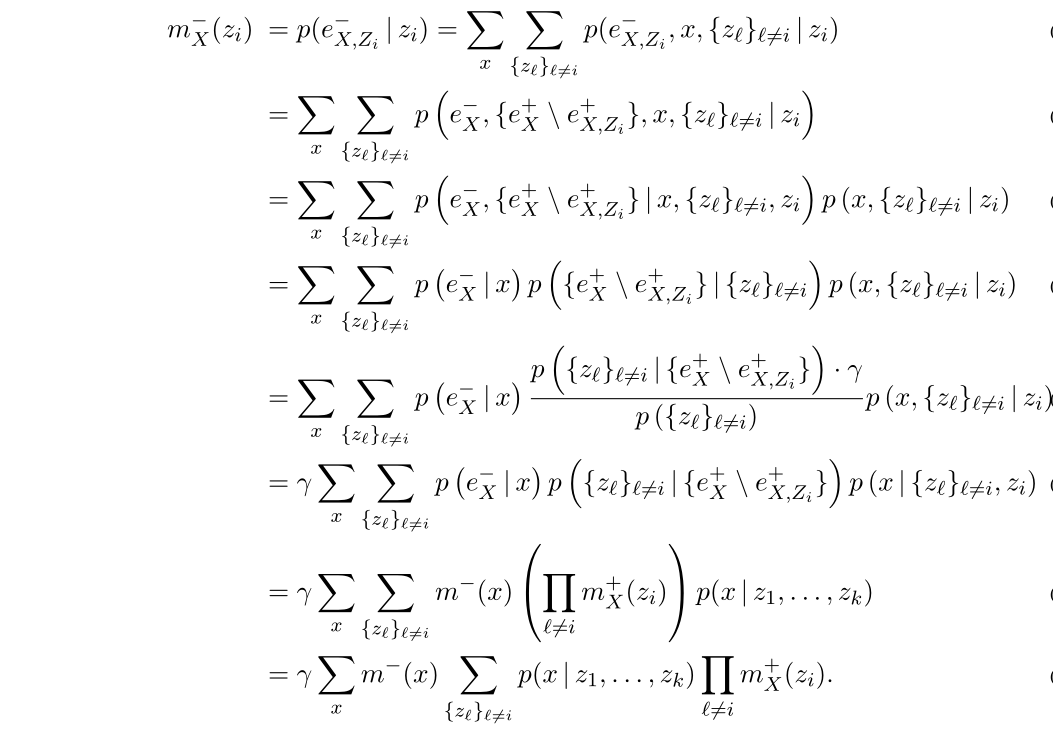有向图模型知识综述
一、图模型基本概念
图为表示一组随机变量之间的独立关系和计算条件概率提供了强有力的支撑。图模型(graphical model) 即为将条件独立结构编码在图中的概率模型,图中的顶点(结点)表示随机变量,而边代表了相关结点之间的条件独立关系。
其中,条件独立性的概念是:设
X
,
Y
,
Z
X,Y,Z
X,Y,Z均为随机变量,当满足
p
(
x
,
y
∣
z
)
=
p
(
x
∣
z
)
p
(
y
∣
z
)
p(x, y|z)=p(x|z)p(y|z)
p(x,y∣z)=p(x∣z)p(y∣z)时,则称
X
,
Y
X,Y
X,Y在给定
Z
Z
Z的条件下相互独立。这意味着,一旦
Z
Z
Z已知,
Y
Y
Y就不提供关于
x
x
x的额外信息。利用条件独立关系可以将联合分布分解简化。
图模型主要分为有向图和无向图,有向图用于表示变量之间的条件独立关系,也可以用来表示因果关系。当图中的边带有方向时,该图就是有向图,反之则为无向图。
二、有向无环图(DAGs)
记有向图
G
=
(
V
,
E
)
G=(V, E)
G=(V,E),其中
V
V
V表示顶点集,
E
E
E表示边集,由于边是有向的,采用有序的顶点对来表示。这里介绍有向图中的几个概念:
(1)相邻:
X
,
Y
X, Y
X,Y 之间有有向边连接,称
X
,
Y
X, Y
X,Y相邻;
(2)父元素/子元素:若
X
→
Y
X→Y
X→Y,称
X
X
X为
Y
Y
Y的父亲,
Y
Y
Y为
X
X
X的孩子;随机变量
X
X
X的所有父元素节点集合记为
π
X
π_X
πX或
π
(
X
)
π(X)
π(X)
(3)祖先/后代:若有一条从
X
X
X到
Y
Y
Y的有向路径,称
X
X
X为
Y
Y
Y的祖先,
Y
Y
Y为
X
X
X的后代
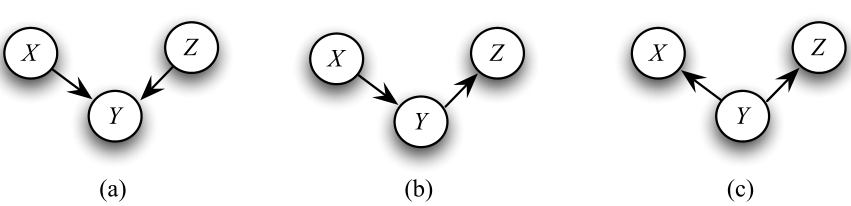
三节点子图基本结构:(1)X→Y←Z(头对头)(2)X→Y→Z(头对尾)(3)X←Y→Z(尾对尾)
碰撞点(collider):路径相关,如图,路径{X,Y,Z}中Y为碰撞点;路径{X,Y,W}中Y不是碰撞点。
有向图中有三个基本的结构,所有的有向图都可以由这三个基本结构拼接而成,如下图所示:
其中,
(
a
)
(a)
(a)图表示的是头对头结构,其中
Y
Y
Y被称为碰撞点(collider);
(
b
)
(b)
(b)图表示的是头对尾结构;
(
c
)
(c)
(c) 图表示的是尾对尾结构。碰撞点指的就是头对头结构中中间的那部分,它是一个路径相关的概念。而当指向碰撞点的两个变量不相邻时,称该碰撞点是非屏蔽的。
开始和结束于同一个变量的有向路径称为循环,如果一个有向图内没有循环,它就是无环的。由于有向有环图上很难提供连贯的概率语义,通常研究有向无环图。
三、概率与DAGs
3.1 DAGs与马尔科夫
令有向无环图
G
=
(
V
,
E
)
,
V
=
(
X
1
,
X
2
,
…
,
X
d
)
G=(V, E), V=(X_1, X_2,…,X_d)
G=(V,E),V=(X1,X2,…,Xd),若
P
P
P为
V
V
V上的概率函数
p
(
x
)
p(x)
p(x)对应的概率分布,当
p
(
x
)
=
∏
j
=
1
d
p
(
x
j
∣
π
x
j
)
p(x)=\prod_{j=1}^{d}p(x_{j}|\pi_{x_j})
p(x)=∏j=1dp(xj∣πxj)时称
G
G
G表征了
P
P
P,
P
P
P到
G
G
G是马尔科夫的,
G
G
G表示的分布集合用
M
(
G
)
M(G)
M(G)表示。
对于图
G
G
G,其分布
P
∈
M
(
G
)
P\in M(G)
P∈M(G)当且仅当马尔科夫条件成立。马尔科夫条件为:对每一变量
W
W
W,在给定
π
W
π_W
πW的条件下,
W
W
W与其他非父元素变量条件独立。
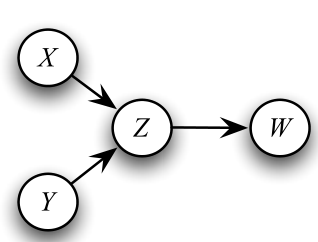
例:如图,当且仅当概率函数满足
p
(
x
,
y
,
z
,
w
)
=
p
(
x
)
p
(
y
)
p
(
z
∣
x
,
y
)
p
(
w
∣
z
)
p(x, y, z, w) = p(x)p(y)p(z | x, y)p(w | z)
p(x,y,z,w)=p(x)p(y)p(z∣x,y)p(w∣z)时,分布
P
∈
M
(
G
)
P\in M(G)
P∈M(G)。
DAGs与马尔科夫的性质有很多应用,如马尔科夫链、隐马尔可夫模型(HMM)、层次模型、随机效应模型(REM)等。
四、独立关系寻找
马尔科夫条件可以帮助列出由DAG隐含的一些独立关系,为了更加全面地找到独立关系,这里引出两个概念
d
−
s
e
p
r
a
t
i
o
n
d-sepration
d−sepration(定向分离)和
d
−
c
o
n
n
e
c
t
e
d
d-connected
d−connected(定向连接)。
判断
d
−
s
e
p
r
a
t
i
o
n
d-sepration
d−sepration 有三条规则:
- 当 Y Y Y不是碰撞点, X , Z X,Z X,Z为 d − c o n n e c t e d d-connected d−connected,但当给定 Y Y Y时, X , Z X,Z X,Z为 d − s e p r a t i o n d-sepration d−sepration
- 当 X , Y X,Y X,Y在 Y Y Y处碰撞, X , Z X,Z X,Z为 d − s e p r a t i o n d-sepration d−sepration,但当给定 Y Y Y时, X , Z X,Z X,Z为 d − c o n n e c t e d d-connected d−connected
- 在碰撞点处的条件作用对碰撞点的后代有相同作用(碰撞点的后代在给定条件集合中时,可消除碰撞点作用)
(参考:http://bayes.cs.ucla.edu/BOOK-2K/d-sep.html)
按照上面三条规则可以判断有向分离,也可以通过更加正式的定义进行判断:
d
−
s
e
p
r
a
t
i
o
n
d-sepration
d−sepration/
d
−
c
o
n
n
e
c
t
e
d
d-connected
d−connected 正式定义:
X
,
Y
X, Y
X,Y为不同的顶点,
W
W
W为若干顶点的集合(不含
X
,
Y
X,Y
X,Y),若在给定
W
W
W的条件下,
X
,
Y
X,Y
X,Y之间存在一条无向路径U满足
①
U
U
U上每个collider的后代都在W中,或 ②
U
U
U上顶点都不在W中,则X, Y在给定W的条件下是
d
−
c
o
n
n
e
c
t
e
d
d-connected
d−connected的;反之,若① ②均不满足,则X, Y在给定W的条件下是
d
−
s
e
p
r
a
t
i
o
n
d-sepration
d−sepration的。
此外,集合间也存在
d
−
s
e
p
r
a
t
i
o
n
d-sepration
d−sepration的概念。集合间的
d
−
s
e
p
r
a
t
i
o
n
d-sepration
d−sepration定义如下:
A
,
B
,
W
A, B, W
A,B,W 是不同顶点集,且
A
A
A 和
B
B
B 不为空。给定
W
W
W的条件下,
A
,
B
A,B
A,B 是
d
−
s
e
p
r
a
t
i
o
n
d-sepration
d−sepration需要满足对每个
X
∈
A
X\in A
X∈A和
Y
∈
B
Y\in B
Y∈B,
X
,
Y
X, Y
X,Y在给定
W
W
W的条件下是
d
−
s
e
p
r
a
t
i
o
n
d-sepration
d−sepration的。
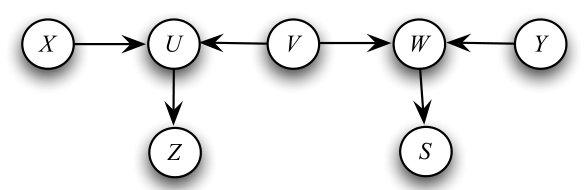
例:如图,由
d
−
s
e
p
r
a
t
i
o
n
d-sepration
d−sepration/
d
−
c
o
n
n
e
c
t
e
d
d-connected
d−connected 的定义和规则可以得出图中存在以下几个有向分离、有向连接关系:
- X X X与 Y Y Y是有向分离的:由于 X X X与 Y Y Y之间存在一条无向路径 X − U − V − W − Y X-U-V-W-Y X−U−V−W−Y,该路径上存在两个collider, U U U和 W W W,由于没有给出额外条件,故这两个collider的后代都不在额外条件里,从而 X X X与 Y Y Y有向分离。
- 给定 Z , S {Z,S} Z,S的条件下, X X X与 Y Y Y是有向连接的:同理,两个collider的后代为 Z , S {Z,S} Z,S,刚好在给定条件的集合内,故 X X X与 Y Y Y是有向连接的。
- 给定
Z
,
S
,
V
{Z,S,V}
Z,S,V的条件下,
X
X
X与
Y
Y
Y是有向分离的:同理,路径上的
V
V
V在给定条件中,故
X
X
X与
Y
Y
Y是有向分离的。
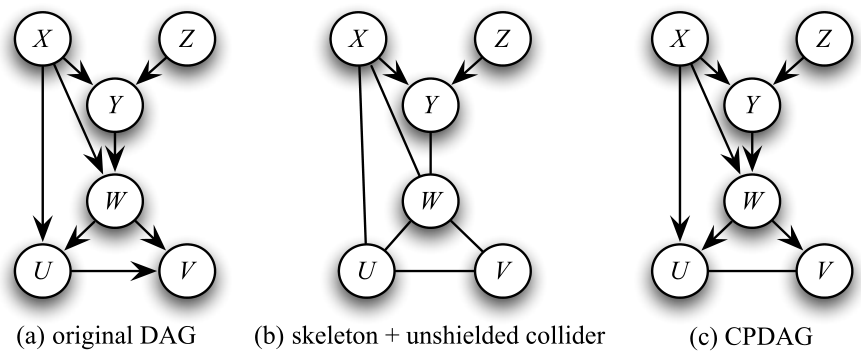
此处,还需要引出一个重要的概念——马尔科夫等价。由于看起来不同的图实际上可能意味着相同的独立关系,这样的两个图是等价的。具体来说, G 1 G_1 G1和 G 2 G_2 G2 为马尔科夫等价当且仅当 ( 1 ) s k e l e t o n ( G 1 ) = s k e l e t o n ( G 2 ) (1)skeleton(G_1)=skeleton(G_2) (1)skeleton(G1)=skeleton(G2),且 ( 2 ) G 1 , G 2 (2)G_1, G_2 (2)G1,G2有相同的非屏蔽collider。
五、高斯DAGs
高斯DAGs目的在于使用有向图模型表示多元高斯分布,这种表示通常是基于线性高斯模型的。首先对几个基本概念进行介绍:
- 线性高斯模型:
Y
Y
Y为DAG中的一个连续变量,其父节点为
X
1
,
…
,
X
k
X_1,…,X_k
X1,…,Xk,当存在参数
β
0
,
β
1
,
…
,
β
k
\beta_0, \beta_1,…, \beta_k
β0,β1,…,βk和
σ
2
\sigma^2
σ2满足下列条件时,称
Y
Y
Y的父节点为线性高斯模型:
Y = β 0 + β 1 X 1 + … + β k X k + ϵ , ϵ ∼ N ( 0 , σ 2 ) Y=\beta_0+\beta_1X_1+…+\beta_kX_k+\epsilon, \epsilon \sim N(0,\sigma^2) Y=β0+β1X1+…+βkXk+ϵ,ϵ∼N(0,σ2) - 高斯有向图模型:若所有变量都连续,且每个变量及其父变量都遵循线性高斯模型,则该有向图模型称为高斯有向图模型(或高斯贝叶斯网络)。(每个节点由其父节点加正态分布随机噪声的线性函数表示)
- 联合多元高斯分布:假设 Y Y Y的父结点 X 1 , … , X k X_1,…,X_k X1,…,Xk满足线性高斯模型,即 Y = β 0 + ∑ j = 1 k β j X j + ϵ , ϵ ∼ N ( 0 , σ 2 ) Y=\beta_0+\sum_{j=1}^{k}\beta_jX_j+\epsilon, \epsilon \sim N(0,\sigma^2) Y=β0+∑j=1kβjXj+ϵ,ϵ∼N(0,σ2),又假设 X = ( X 1 , … , X k ) X=(X_1,…,X_k) X=(X1,…,Xk)满足联合高斯分布 N ( μ , ∑ ) N(\mu,\sum) N(μ,∑),则联合分布 ( Y , X 1 , … , X k ) (Y, X_1,…,X_k) (Y,X1,…,Xk)是协方差为 C o v ( Y , X i ) = ∑ j = 1 k β j ∑ i j Cov(Y,X_i)=\sum_{j=1}^k\beta_j\sum_{ij} Cov(Y,Xi)=∑j=1kβj∑ij的高斯分布,此外,期望 E ( Y ) = β 0 + β T μ E(Y)=\beta_0+\beta^T\mu E(Y)=β0+βTμ,方差 V a r ( Y ) = σ 2 + β T ∑ β Var(Y)=\sigma^2+\beta^T\sum\beta Var(Y)=σ2+βT∑β,其中 β = ( β 1 , … , β k ) \beta=(\beta_1,…,\beta_k) β=(β1,…,βk)。这个定理证明了任何的高斯贝叶斯网络都可以转换为高斯多元分布。
- 反命题(任何多元高斯分布都可以转换为高斯贝叶斯网络): P P P为 d d d维多元高斯随机向量 X = ( X 1 , … , X d ) X=(X_1,…,X_d) X=(X1,…,Xd)的联合分布,对 X X X的任意顺序,可以构造出DAG图 G G G使 P P P到 G G G是马尔科夫的。
基于以上几个概念和定理,此处再引出高斯模型的条件独立性概念:
首先介绍偏相关系数的概念:
ρ
X
,
Y
∣
Z
\rho_{X,Y|Z}
ρX,Y∣Z是变量
X
,
Y
X, Y
X,Y在给定的另一组变量
Z
=
(
Z
1
,
Z
2
,
…
,
Z
k
)
Z=(Z_1,Z_2,…,Z_k)
Z=(Z1,Z2,…,Zk)上,对
X
,
Y
X,Y
X,Y分别进行回归产生的残差之间的相关性。公式为:
ρ
X
,
Y
∣
Z
=
E
(
X
Y
∣
Z
)
−
E
(
X
∣
Z
)
E
(
Y
∣
Z
)
V
a
r
(
X
∣
Z
)
V
a
r
(
Y
∣
Z
)
\rho_{X,Y|Z}=\frac{\mathbb{E}(XY|Z)-\mathbb{E}(X|Z)\mathbb{E}(Y|Z)}{\sqrt{Var(X|Z)}\sqrt{Var(Y|Z)}}
ρX,Y∣Z=Var(X∣Z)Var(Y∣Z)E(XY∣Z)−E(X∣Z)E(Y∣Z)
由多元高斯分布的偏相关系数可以推导出高斯模型的条件独立性,由下面这个定理阐释:
定理:
X
=
(
X
1
,
…
,
X
d
)
X=(X_1,…,X_d)
X=(X1,…,Xd)为高斯随机向量,对
i
≠
j
∈
{
1
,
…
,
d
}
,
K
⊂
{
1
,
…
,
d
}
/
{
i
,
j
}
i\neq j\in\{1,…,d\},K\subset\{1,…,d\} / \{i,j\}
i=j∈{1,…,d},K⊂{1,…,d}/{i,j},定义在给定
{
X
k
:
k
∈
K
}
\{X_k:k\in K\}
{Xk:k∈K}时,
X
i
X_i
Xi和
X
j
X_j
Xj之间的偏相关系数为
ρ
i
,
j
∣
K
\rho_{i,j|K}
ρi,j∣K。
ρ
i
,
j
∣
K
=
0
\rho_{i,j|K}=0
ρi,j∣K=0当且仅当在给定
{
X
k
:
k
∈
K
}
\{X_k:k\in K\}
{Xk:k∈K}的条件下,
X
i
X_i
Xi和
X
j
X_j
Xj条件独立。
六、精确推理
有向图常用于推断,而其中某些结点作为证据节点被设定为固定值,则希望能够计算出其他一些变量的后验分布。通常这样的计算代价很高,而基于DAGs提出了第一个有效的使用消息传递体系结构来进行概率推理的算法——置信度传播算法(信念传播算法/和-积算法)。
首先,介绍置信度传播算法的几个概念:
- 预假设:所有变量离散,求边缘概率等价于求和。(对连续变量,求和即为求积分)
- polytree:polytree是任意两个节点之间最多只有一条无向路径的有向图。(即,polytree为没有无向环的DAG)通常在polytree上进行精确推理。
- 推理问题形式: P ( X = x ∣ E = e ) \mathbb{P}(X=x|E=e) P(X=x∣E=e), X X X是一个查询节点, E E E是被设置为某个值的观察节点(证据节点)的任意子集。
基于此,可以进行信念传播算法的递归关系计算:
设
E
=
E
X
+
∪
E
X
−
E=E^+_X\cup E^-_X
E=EX+∪EX−,其中
E
X
+
E^+_X
EX+是
X
X
X祖先节点的子集,
E
X
−
E^-_X
EX−是
X
X
X后代节点的子集。将每个节点视为一个处理器,它接收来自其邻居的消息,并在经过一些局部计算后将其传递。
设
X
X
X 有
n
n
n 个孩子
Y
1
,
…
,
Y
n
Y_1,…,Y_n
Y1,…,Yn 和
k
k
k 个父亲
Z
1
,
…
,
Z
k
Z_1,…,Z_k
Z1,…,Zk,
X
X
X从孩子
Y
j
Y_j
Yj 处接收到的信息记为
m
Y
j
−
(
X
)
m_{Y_j}^-(X)
mYj−(X),又记
m
Y
j
+
(
X
)
m_{Y_j}^+(X)
mYj+(X)为从
X
X
X发送到
Y
j
Y_j
Yj 处的信息;同理,
m
X
−
(
Z
j
)
m_X^-(Z_j)
mX−(Zj) 为
X
X
X 发送到
Z
j
Z_j
Zj 处的信息,
m
X
+
(
Z
j
)
m_X^+(Z_j)
mX+(Zj) 为父亲
Z
j
Z_j
Zj从
X
X
X处接收到的信息。
令
E
X
+
=
e
X
+
E^+_X=e^+_X
EX+=eX+,
E
X
−
=
e
X
−
E^-_X=e^-_X
EX−=eX−,
p
(
x
∣
e
X
+
,
e
X
−
)
≡
P
(
X
=
x
∣
E
X
+
=
e
X
+
,
E
X
−
=
e
X
−
)
p(x|e^+_X,e^-_X)\equiv\mathbb{P}(X=x|E^+_X=e^+_X,E^-_X=e^-_X)
p(x∣eX+,eX−)≡P(X=x∣EX+=eX+,EX−=eX−) ,
由于
X
X
X 将
E
X
+
E^+_X
EX+ 和
E
X
−
E^-_X
EX−定向分离,
p
(
e
X
+
,
e
X
−
∣
x
)
=
p
(
e
X
+
∣
x
)
p
(
e
X
−
∣
x
)
p(e^+_X,e^-_X|x)=p(e^+_X|x)p(e^-_X|x)
p(eX+,eX−∣x)=p(eX+∣x)p(eX−∣x)
进一步定义
E
X
+
=
E
X
,
Z
1
+
∪
…
∪
E
X
,
Z
k
+
E^+_X=E^+_{X,Z_1}\cup…\cup E^+_{X,Z_k}
EX+=EX,Z1+∪…∪EX,Zk+,其中
E
X
,
Z
i
+
为
E
X
+
E^+_{X,Z_i}为E^+_{X}
EX,Zi+为EX+的一个子集,也是
Z
i
Z_i
Zi的祖先;
同理定义
E
X
−
=
E
X
,
Y
1
−
∪
…
∪
E
X
,
Y
n
−
E^-_X=E^-_{X,Y_1}\cup…\cup E^-_{X,Y_n}
EX−=EX,Y1−∪…∪EX,Yn−,其中
E
X
,
Y
i
−
为
E
X
−
E^-_{X,Y_i}为E^-_{X}
EX,Yi−为EX−的一个子集,也是
Y
j
Y_j
Yj的后代。
定义
m
+
(
x
)
≡
p
(
x
∣
e
X
+
)
m^+(x)\equiv p(x|e^+_X)
m+(x)≡p(x∣eX+)为传播的
E
X
+
=
e
X
+
E^+_X=e^+_X
EX+=eX+,
X
X
X从它的父亲那里得到
E
X
+
=
e
X
+
E^+_X=e^+_X
EX+=eX+并传播给孩子;
同理,
m
−
(
x
)
≡
p
(
x
∣
e
X
−
)
m^-(x)\equiv p(x|e^-_X)
m−(x)≡p(x∣eX−)为传播的
E
X
−
=
e
X
−
E^-_X=e^-_X
EX−=eX−,
X
X
X从它的孩子那里得到
E
X
−
=
e
X
−
E^-_X=e^-_X
EX−=eX−并传播给父亲。
计算时利用了
X
X
X定向分离
Y
1
,
Y
2
,
…
,
Y
n
Y_1,Y_2,…,Y_n
Y1,Y2,…,Yn这一性质。且由上述公式可知,计算通过节点
X
X
X向父节点、子节点传递的消息,可以算出答案。那么问题就转换为如何计算X收发的消息,即计算
m
Y
j
+
(
X
)
m_{Y_j}^+(X)
mYj+(X)和
m
X
−
(
Z
j
)
m_X^-(Z_j)
mX−(Zj)。
X
X
X 发给孩子节点
Y
j
Y_j
Yj的信息包括:
X
X
X从父亲处获得(即
E
X
+
E^+_X
EX+);
X
X
X从其它孩子处获得(即
E
X
−
\
E
X
,
Y
j
−
E^-_X \backslash E^-_{X,Y_j}
EX−\EX,Yj−)则
m
Y
j
+
(
X
)
m_{Y_j}^+(X)
mYj+(X) 可由下式推导:注意:
β
=
1
p
(
{
e
X
−
\
e
X
,
Y
j
−
}
∣
e
X
+
)
\beta=\frac{1}{p(\{e_X^-\backslash e_{X,Y_j}^-\}|e_X^+)}
β=p({eX−\eX,Yj−}∣eX+)1,且
X
X
X 定向分离各孩子节点。
同理,父亲节点
Z
i
Z_i
Zi从
X
X
X收到的信息包括:
X
X
X从孩子处获得的
E
X
−
E_X^-
EX−,
X
X
X从其它父亲处获得的
E
X
−
\
E
X
,
Z
i
−
E_X^-\backslash E_{X,Z_i}^-
EX−\EX,Zi−,同样可以计算出
m
X
−
(
Z
i
)
m^-_X(Z_i)
mX−(Zi)。
在确定递归关系后,还需要确定递归初始值。注意到:叶节点没有孩子;根节点没有父亲;证据节点若被初始化为某个证据值e,则该节点收发信息值均设为1;未初始化的叶节点,将发给其父亲的信息均设为1;未初始化的根结点,发送给其孩子的信息设为
P
(
x
)
\mathbb{P}(x)
P(x)。
至此,信念传播算法的流程就结束了。
而为了解决最大化概率问题,或为某些观察找到最可能的解释(即最大后验估计),一个名为最大积(最大和)的算法被提出。在此算法中,问题被形式化为
x
^
=
a
r
g
m
a
x
x
P
(
X
=
x
∣
E
=
e
)
\widehat{x}=\underset{x}{argmax}\mathbb {P}(X=x|E=e)
x
=xargmaxP(X=x∣E=e)。算法的总体流程类似信念传播算法,只是将计算消息时将结点收到的消息的总和变为消息的最大值。
七、近似推理
为了解决图中包含循环的问题,提出了近似推理的方法,包括变分法(确定性算法);抽样法(随机性算法);疯狂信念传播算法(不能保证收敛)。
八、标准参数估计
标准参数估计是在给定DAG图
G
G
G的情况下,估计联合分布的参数,可以大致分为两类:全观测数据的参数估计和带有隐变量的参数估计。
8.1 全观测数据的参数估计
假设对每个条件密度,参数模型为
p
(
x
j
∣
π
x
j
;
θ
j
)
p(x_j|\pi_{x_j};\theta_j)
p(xj∣πxj;θj),其中,
θ
=
(
θ
1
,
…
,
θ
d
)
\theta=(\theta_1,…,\theta_d)
θ=(θ1,…,θd)为一组参数,则联合分布可表示为:
p
(
x
;
θ
)
=
∏
j
=
1
d
p
(
x
j
∣
π
x
j
;
θ
j
)
p(x;\theta)=\prod_{j=1}^{d}p(x_j|\pi_{x_j};\theta_j)
p(x;θ)=∏j=1dp(xj∣πxj;θj)
若给定
n
n
n 个观测点
{
x
1
,
…
,
x
n
}
\{x_1,…,x_n\}
{x1,…,xn},似然函数可表示为:
L
(
θ
)
=
∏
i
=
1
n
p
(
x
i
;
θ
)
=
∏
i
=
1
n
∏
j
=
1
d
p
(
x
i
j
∣
π
x
j
;
θ
j
)
L(\theta)=\prod_{i=1}^np(x_i;\theta)=\prod_{i=1}^n\prod_{j=1}^dp(x_{ij}|\pi_{x_j};\theta_j)
L(θ)=∏i=1np(xi;θ)=∏i=1n∏j=1dp(xij∣πxj;θj)
通过最大似然可以估计参数,对数似然分解如下:
l
(
θ
)
=
l
o
g
L
(
θ
)
=
∑
j
=
1
d
l
o
g
(
∏
i
=
1
n
p
(
x
i
j
∣
π
x
j
;
θ
j
)
≡
∑
j
=
1
d
l
o
g
L
j
(
θ
j
)
=
∑
j
=
1
d
l
j
(
θ
j
)
l(\theta)=logL(\theta)=\sum_{j=1}^dlog(\prod_{i=1}^np(x_{ij}|\pi_{x_j};\theta_j)\equiv\sum_{j=1}^dlogL_j(\theta_j)=\sum_{j=1}^dl_j(\theta_j)
l(θ)=logL(θ)=∑j=1dlog(∏i=1np(xij∣πxj;θj)≡∑j=1dlogLj(θj)=∑j=1dlj(θj)
其中,
l
j
(
θ
j
)
=
∑
i
=
1
n
l
o
g
p
(
x
i
j
∣
π
x
j
;
θ
j
)
l_j(\theta_j)=\sum_{i=1}^nlogp(x_{ij}|\pi_{x_j};\theta_j)
lj(θj)=∑i=1nlogp(xij∣πxj;θj)是
θ
j
\theta_j
θj的局部条件似然。
8.2 带有隐变量的参数估计
观察到的数据可能不包括DAG中某些变量的值,称这些变量为隐藏变量。
若
Z
Z
Z表示隐变量,则对数似然可写为:
l
(
θ
)
=
∑
i
=
1
n
l
o
g
p
(
x
i
;
θ
)
=
∑
i
=
1
n
l
o
g
∫
z
i
p
(
x
i
,
z
i
;
θ
)
d
z
i
l(\theta)=\sum_{i=1}^nlogp(x_{i};\theta)=\sum_{i=1}^nlog\int_{z_i}p(x_i,z_i;\theta)dz_i
l(θ)=∑i=1nlogp(xi;θ)=∑i=1nlog∫zip(xi,zi;θ)dzi,
由于隐变量的存在,就无法直接进行分解求值,通常采用最大化方法——EM算法
九、结构学习
为了从数据中估计DAG,主流方法有两类:(1)基于约束的方法:使用统计测试从数据中学习条件独立关系(约束),并使用获得的约束修剪图搜索空间;(2)基于分数的算法:给每个候选DAG分配一个反映其拟合优度的分数,然后将其作为一个目标函数进行优化。其中,PC算法作为基于约束的方法,效果非常优越,下面主要介绍PC算法。
首先介绍一个重要的概念——代表等价类。
设
X
X
X为
d
d
d维随机向量,分布为
P
P
P,假设存在一个
G
G
G使
P
P
P关于
G
G
G是忠实的。由马尔科夫等价定理,无需确定单一的
G
G
G,只需确定
G
G
G的等价类。
等价类采用带有非屏蔽碰撞点标记的骨架图来表示,除了对应于非屏蔽碰撞点的边,所有边无向。通过对无向骨架图的非屏蔽碰撞点对应边加方向,得到PDAG,再通过简单的规则可以判断PDAG中某些无向边的方向是否确定,如:不能引入新的collider;不能引入环等得到CPDAG.
- 部分有向无环图(PDAG):包含有向边和无向边的无环图,不能通过跟随有向边的方向和无向边的任何方向来跟踪一个环。
- CPDAG:若G为DAG,K为PDAG,当满足下列两个条件时,K是一个完全PDAG(CPDAG):(1)
s
k
e
l
e
t
o
n
(
K
)
=
s
k
e
l
e
t
o
n
(
G
)
skeleton(K)=skeleton(G)
skeleton(K)=skeleton(G) (2)K所包含一条有向边当且仅当与
G
G
G等价的DAG包含有相同的有向边。
给定一个忠于 G G G的分布 P P P,只能确定 G G G的CPDAG
接下来正式介绍PC算法,PC算法就是输入分布P,输出对应的CPDAG。它分为两个步骤:(1)识别DAG骨架:从完整的无向图,基于条件独立决策递归地删除边,生成无向骨架图;(2)确定CPDAG:对其进行部分定向并进一步扩展以表示CPDAG。
步骤1 识别DAG骨架:
此步骤目标是构建无向图 S S S使得 S = s k e l e t o n ( G ) S=skeleton(G) S=skeleton(G)。这一步骤基于条件独立关系,即在给定不同的变量子集 A A A的条件下, X i X_i Xi和 X j X_j Xj条件独立 ( X i ⊥ X j ∣ A ) (X_i\bot X_j|A) (Xi⊥Xj∣A)。
这里需要引入定理: G G G为DAG,分布 P P P忠实于 G G G,若 X i X_i Xi与 X j X_j Xj在 G G G中相邻,对任意 A A A, X i X_i Xi和 X j X_j Xj条件独立不成立。另一方面,若 X i X_i Xi和 X j X_j Xj不相邻,要么 X i ⊥ X j ∣ π ( X i ) X_i\bot X_j|\pi(X_i) Xi⊥Xj∣π(Xi),要么 X i ⊥ X j ∣ π ( X j ) X_i\bot X_j|\pi(X_j) Xi⊥Xj∣π(Xj)
由这一定理,只需检查是否存在 A ⊂ V \ { i , j } A\subset V\backslash\{i,j\} A⊂V\{i,j} 使 X i ⊥ X j ∣ A X_i\bot X_j|A Xi⊥Xj∣A,若存在, X i X_i Xi和 X j X_j Xj相邻,称 A A A为对应 X i X_i Xi和 X j X_j Xj的分离集。
此外,若 X i ⊥ X j ∣ A X_i\bot X_j|A Xi⊥Xj∣A,对 A A A的任意超集 A ′ A' A′, X i ⊥ X j ∣ A ′ X_i\bot X_j|A' Xi⊥Xj∣A′。由此,可以按照大小递增的顺序搜索可能的分离集。
则步骤1的总体算法如下图:为了确保 X i X_i Xi和 X j X_j Xj相邻,要对所有可能的 A A A遍历检查。算法中, a d j ( C , i ) adj(C,i) adj(C,i)代表初始无向图 C C C中 X i X_i Xi的邻接节点。 k k k为分离集的大小,上限 d d d取决于 s k e l e t o n ( G ) skeleton(G) skeleton(G)的最大度 K K K。有 研究证明 d = K − 1 d=K-1 d=K−1或 d = K d=K d=K。
步骤2:确定CPDAG
确定CPDAG的关键在于识别非屏蔽碰撞点,由此提出非屏蔽collider确定定理:
非屏蔽collider确定定理:假设从PC算法步骤1输出骨架为 C C C,一组分离集为 A A A。候选关系 X i − X k − X j X_i-X_k-X_j Xi−Xk−Xj 当且仅当 X k ∉ A i j X_k\notin A_{ij} Xk∈/Aij :时为非屏蔽collider X i → X k ← X j X_i\rightarrow X_k\leftarrow X_j Xi→Xk←Xj(通过反证法证明)
确定非屏蔽collider后可获得 PDAG。
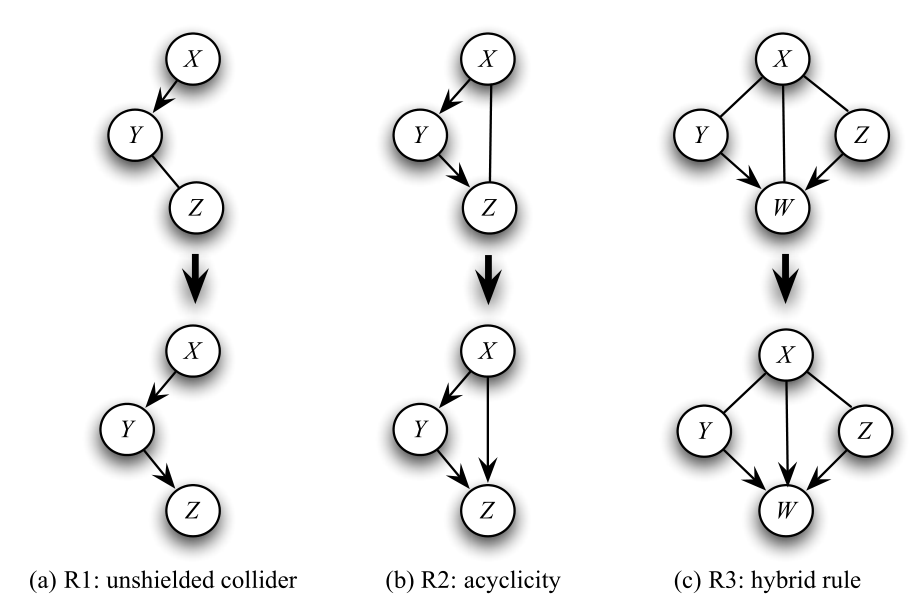
接下来需要继续确定图中某些边的方向:通过三个规则,匹配PDAG中符合条件的三个初始子图应用规则来确定。
●Rule1:若构型 X → Y − Z X\rightarrow Y-Z X→Y−Z不是非屏蔽collider,则必为 X → Y → Z X\rightarrow Y\rightarrow Z X→Y→Z
●Rule2:DAG中不允许环的存在。
●Rule3:Rule1和Rule1的结合,若存在有向边 W → X W\rightarrow X W→X,则必有 Y → X Y\rightarrow X Y→X, Z → X Z\rightarrow X Z→X,而这又导致出现新的非屏蔽collider Y → X ← Z Y\rightarrow X\leftarrow Z Y→X←Z,不成立,故有向边 W → X W\rightarrow X W→X必不存在,只能是 W ← X W\leftarrow X W←X。
PC算法步骤2的收敛性是显然的,其总体算法如下:
样本版本的PC算法
与前述的总体PC算法不同,若只有观测到的部分数据点的情况下,还想检验 X i ⊥ X j ∣ A X_i\bot X_j|A Xi⊥Xj∣A是否成立应该如何实现?
这一问题对于高斯DAG是易于构造实现的。前面提到过,高斯DAG有定理证明: X i ⊥ X j ∣ A X_i\bot X_j|A Xi⊥Xj∣A当且仅当 ρ i , j ∣ A = 0 \rho_{i,j|A}=0 ρi,j∣A=0, ρ i , j ∣ A \rho_{i,j|A} ρi,j∣A为给定 A A A的条件下, X i X_i Xi和 X j X_j Xj的偏相关系数。为了验证 X i ⊥ X j ∣ A X_i\bot X_j|A Xi⊥Xj∣A,只需进行假设检验:
H 0 : ρ i , j ∣ A = 0 v s . H 1 : ρ i , j ∣ A ≠ 0 H_0: \rho_{i,j|A}=0 \space\space\space\space vs.\space\space\space H_1:\rho_{i,j|A}\neq0 H0:ρi,j∣A=0 vs. H1:ρi,j∣A=0
假设检验的方式为:
令 ρ ^ i , j ∣ A \widehat\rho_{i,j|A} ρ i,j∣A为通过递归公式求解出的样本偏相关系数,
采用费雪变换来进行假设检验,即
令 z ^ i j ∣ A = 1 2 l o g ( 1 + ρ ^ i , j ∣ A 1 − ρ ^ i , j ∣ A ) , z i j ∣ A = 1 2 l o g ( 1 + ρ i , j ∣ A 1 − ρ i , j ∣ A ) \widehat z_{ij|A}=\frac{1}{2}log(\frac{1+\widehat\rho_{i,j|A}}{1-\widehat\rho_{i,j|A}}),z_{ij|A}=\frac{1}{2}log(\frac{1+\rho_{i,j|A}}{1-\rho_{i,j|A}}) z ij∣A=21log(1−ρ i,j∣A1+ρ i,j∣A),zij∣A=21log(1−ρi,j∣A1+ρi,j∣A)。
经典分布理论在高斯情况下刻画了 z ^ i j ∣ A \widehat z_{ij|A} z ij∣A的渐进分布
( n − ∣ A ∣ − 3 ) ( z ^ i j ∣ A − z i j ∣ A ) → D N ( 0 , 1 ) (\sqrt{n-|A|-3})(\widehat z_{ij|A}-z_{ij|A})\overset{D}{\rightarrow}N(0,1) (n−∣A∣−3)(z ij∣A−zij∣A)→DN(0,1), ∣ A ∣ |A| ∣A∣表示 A A A的基数,
而在零假设下, z i j ∣ A = 0 z_{ij|A}=0 zij∣A=0,则利用 α \alpha α测试,但满足下列式子时拒绝零假设:
( n − ∣ A ∣ − 3 ) ∣ z ^ i j ∣ A ∣ > ϕ − 1 ( 1 − α 2 ) (\sqrt{n-|A|-3})|\widehat z_{ij|A}|>\phi^{-1}(1-\frac{\alpha }{2}) (n−∣A∣−3)∣z ij∣A∣>ϕ−1(1−2α),
其中 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅)为标准高斯随机变量的累积函数。
十、DAG应用
故障分析
DAG是一个对不确定性进行推理的工具,几乎所有的领域涉及到预测、智能推理、诊断、决策、风险/可靠性分析的问题都可以运用它来处理。
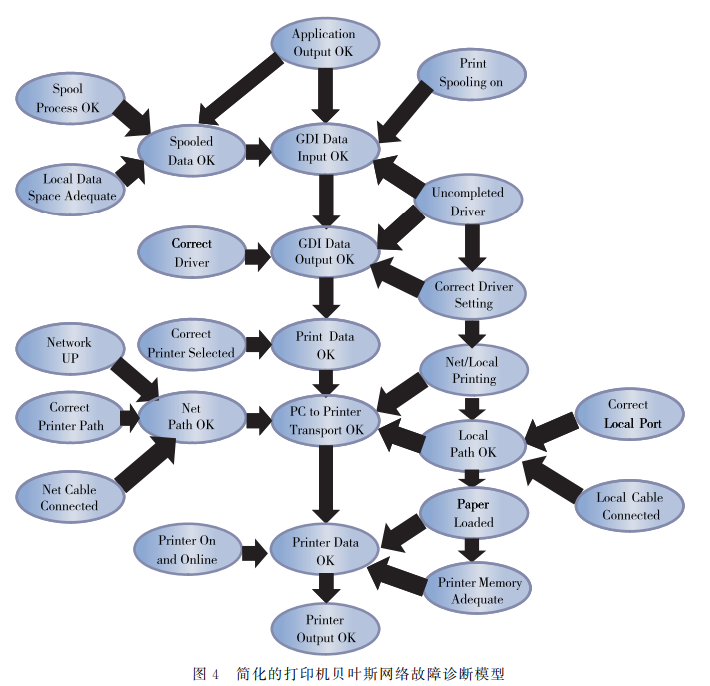
DAG在故障诊断方面有着很大用处,如打印机故障诊断。有研究者提出了一个确定询问-测试修理顺序的框架性的方法。通过不断计算在不同步骤下可能需要的维修方案的功效确定最优的维修路径。在此运用中,DAG 用于更新给定观察证据后的各个故障源的概率,同时诊断过程将修复故障源所需的花费和故障源可能发生的概率综合加以考虑来给出优化的诊断方案。上图就是用于打印机故障诊断的简化的 DAG模型。
常规的DAG诊断模型通常只采用领域专家提供的前向条件概率(从故障源到征兆),还存在利用专家提供的双向条件概率去建立诊断模型,使模型更完备、准确。