目录
一、回溯法理论基础
回溯是递归的副产品,只要有递归就会有回溯,所以回溯法也经常和二叉树遍历,深度优先搜索混在一起,因为这两种方式都是用了递归。
回溯法就是暴力搜索,并不是什么高效的算法,最多再剪枝一下。
回溯算法能解决如下问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 棋盘问题:N皇后,解数独等等
参考代码随想录,针对大部分回溯问题都可以用回溯三部曲来分析并解决问题,模板如下:
void backTrack(需要遍历的原数据,每层遍历的起始参数)
{
if(终止当前层继续遍历的条件)
{
存放结果;
return;
}
for(遍历本层集合的中元素)
{
处理节点;
backTrack(需要遍历的原数据,每层遍历的起始参数);//递归
回溯,撤销处理结果;
}
}二、组合问题
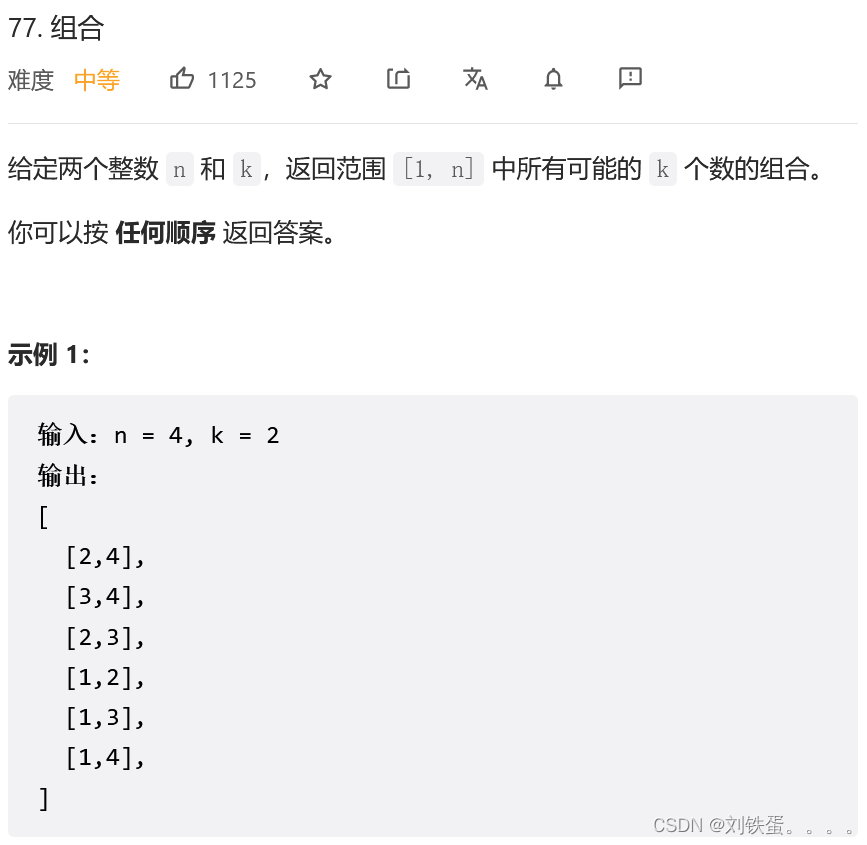
题目:77.组合
class Solution {
public:
vector<vector<int>> result;
vector<int>array;
void backTrack(int n, int k,int start)
{
//退出条件:收集结果的数组元素个数==k
if(array.size()>=k)
{
result.push_back(array);
return;
}
//对于当前层进行遍历
for(int i=start;i<=n;i++)
{
//将当前层贡献节点压入收集结果数组
array.push_back(i);
//递归,为避免多层之间贡献相同索引元素,采用startIndex=i+1
backTrack(n, k, i+1);
//回溯,撤回当前层的操作
array.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
int start=1;
backTrack(n, k, start);
return result;
}
};题目:216.组合总和|||
class Solution {
public:
vector<vector<int>> result;
vector<int> array;
int sum=0;
void backTrack(int start,int k,int target)
{
if(sum>target||(array.size()==k&&sum<target))
return;
if(sum==target&&array.size()==k)
{
result.push_back(array);
return;
}
for(int i=start;i<=9;i++)
{
array.push_back(i);
sum+=i;
backTrack(i+1,k,target);
array.pop_back();
sum-=i;
}
}
vector<vector<int>> combinationSum3(int k, int n) {
backTrack(1,k,n);
return result;
}
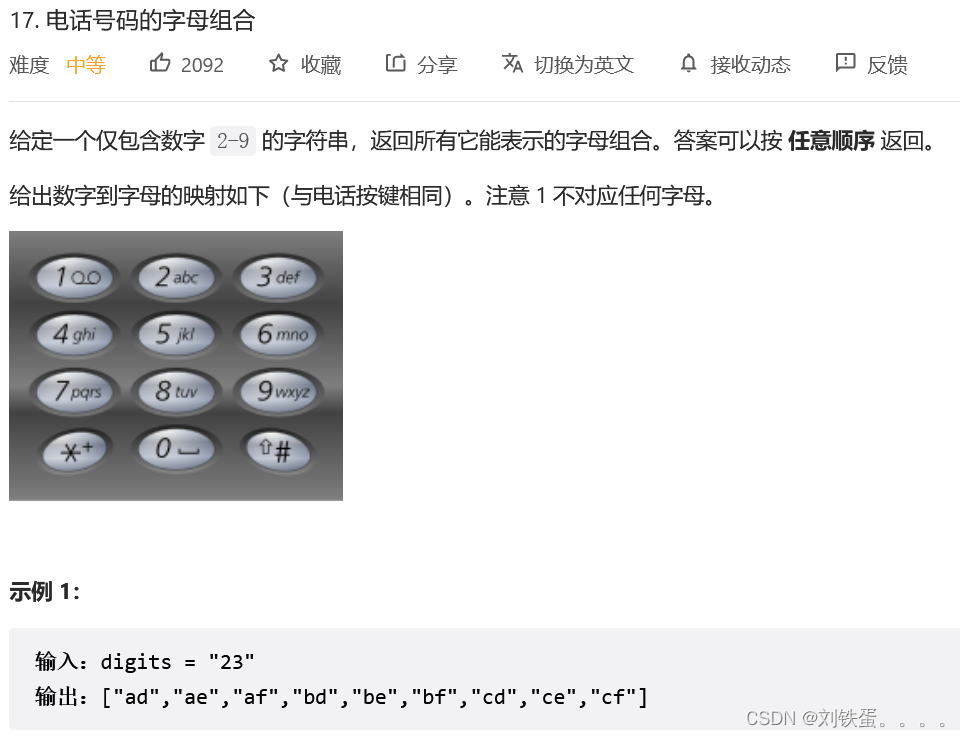
};题目:17.电话号码的字母组合
class Solution {
public:
//每个电话号码代表一层,初始化每一层的元素
vector<string> sample={"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
vector<string> result;
string temp;
void backTrack(string digits,int start)
{
//退出条件:收集结果的字符串长度==给定电话号码个数
if(temp.length()==digits.length())
{
result.push_back(temp);
return;
}
//遍历号码层
for(int i=start;i<digits.length();i++)
{
int num=(digits[i]-'0')-2;
//遍历每个号码对应的字符
for(int j=0;j<sample[num].length();j++)
{
temp+=sample[num][j];//获取当前字符
//递归,,为避免多层之间贡献相同索引元素,采用startIndex=i+1
backTrack(digits,i+1);
temp.resize(temp.size()-1);//删除字符串最后一个子字符
}
}
}
vector<string> letterCombinations(string digits) {
int start=0;
if(digits.length()==0)
return result;
backTrack(digits,start);
return result;
}
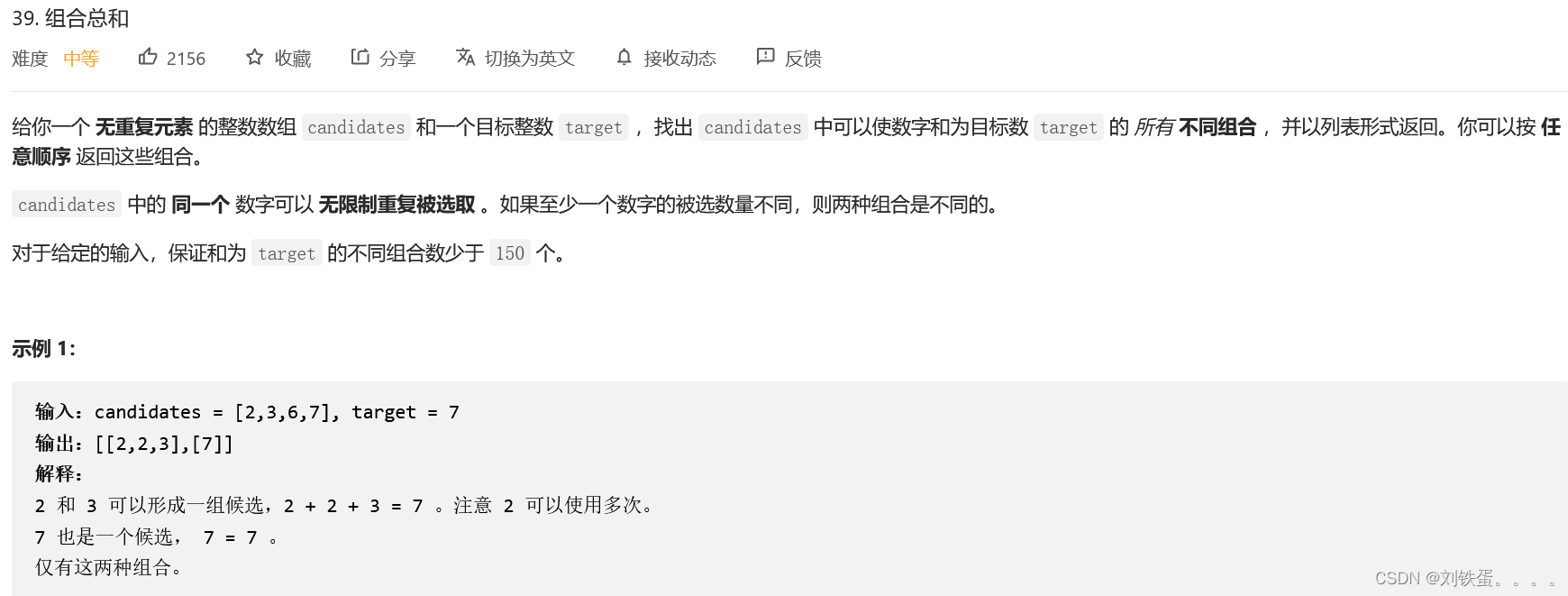
};题目:39.组合总和
class Solution {
public:
vector<int>array;
vector<vector<int>> result;
int sum=0;
void backTrack(vector<int>& candidates, int target,int start)
{
//退出条件:收集结果数组中的元素之和==target
if(sum==target)
{
result.push_back(array);
return;
}
//注意:如果选取的组合元素总和不是恰好等于target,而是大于target则退出当前层
else if(sum>target)
return;
//遍历当前层
for(int i=start;i<candidates.size();i++)
{
sum+=candidates[i];
array.push_back(candidates[i]);
//此处的startIndex==i,是因为需要重复计算同一元素,且要求的是组合,不是排列,
//所以要避免[2,2,3]和[2,3,2]重复出现
backTrack(candidates, target, i);
//回溯,撤回对当前层的操作
sum-=candidates[i];
array.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
int start=0;
backTrack(candidates, target, start);
return result;
}
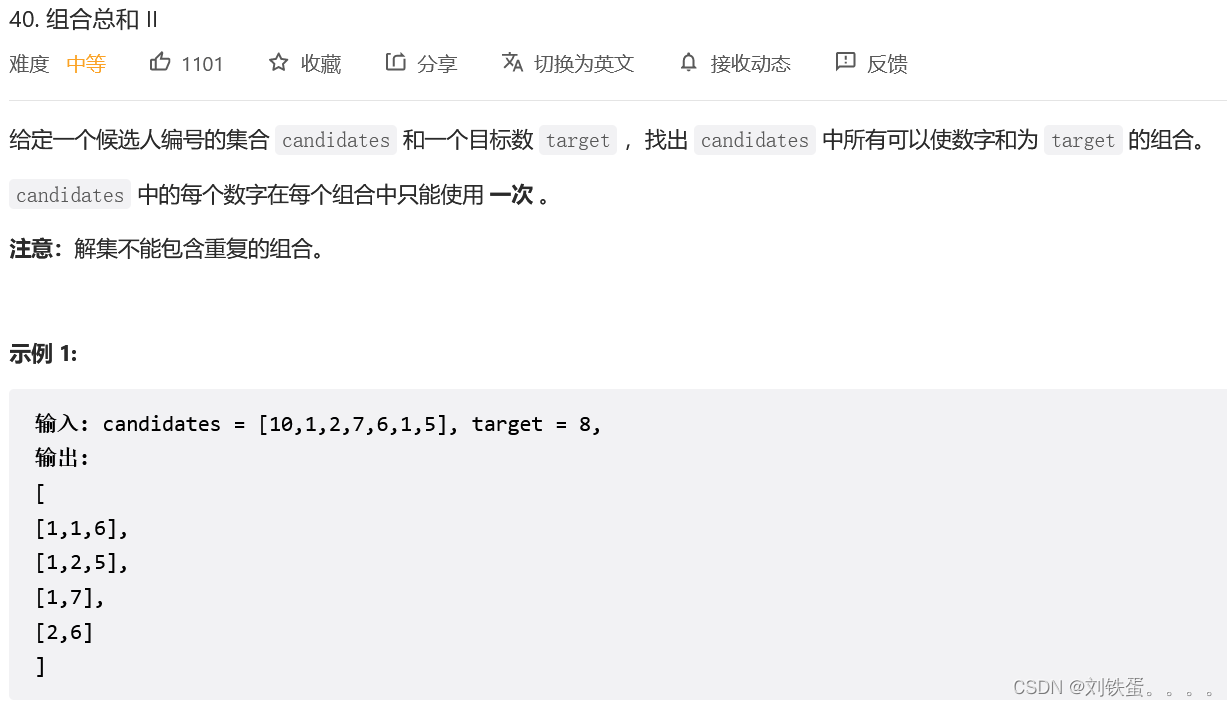
};题目:40.组合总和||
class Solution {
public:
vector<int>array;
vector<vector<int>> result;
int sum=0;
void backTrack(vector<int>& candidates, int target,int start)
{
//退出条件:收集结果数组中的元素之和==target
if(sum==target)
{
result.push_back(array);
return;
}
//注意:如果选取的组合元素总和不是恰好等于target,而是大于target则退出当前层
else if(sum>target)
return;
//遍历当前层
for(int i=start;i<candidates.size();i++)
{
//如果原数据集中存在相同的元素,则这一句很重要【a、b仅用于区别两个3】
//eg:candidates={1,2,3a,3b,4,5} target=9
//会出现[1,3a,5],[1,3b,5]两种重复的情况
if(i>start&&candidates[i]==candidates[i-1])
continue;
sum+=candidates[i];
array.push_back(candidates[i]);
//递归,,为避免多层之间贡献相同索引元素,采用startIndex=i+1
backTrack(candidates, target, i+1);
//回溯,撤回对当前层的操作
sum-=candidates[i];
array.pop_back();
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
int start=0;
//【注意:如果是原数组中出现重复元素,需要同层元素去重,则必须先将原数组继续排序】
sort(candidates.begin(),candidates.end());
backTrack(candidates, target, start);
return result;
}
};题目:494.目标和
有以下两点需要主要:
1.在满足sum==aim后,累加满足目标和的集合个数,此时不可return返回,因为如果aim==0,当sum=aim后,可能此时该数后面还有元素nums[i]=0,可以加入到该集合中,组成新的集合。如果return将会错失这种情况;
2.此处不需要同层去重,同层去重也会导致情况丢失,如:nums={1,1,1,1,1},aim=3;
如果同层去重将会导致类似于{nums[0],nums[1],nums[2]},{nums[0],nums[1],nums[3]}两种情况不可兼得。
class Solution {
private:
int sum;
int count;
void backtracking(vector<int>& nums, int aim,int start)
{
if(sum==aim)
{
count++;
// return;//求数组中元素和为target的集合个数,特殊情况
//当target=0且原数组中存在多个0时,此时不需要返回条件中的return
}
for(int i=start;i<nums.size();i++)
{
sum+=nums[i];
backtracking(nums, aim,i+1);
sum-=nums[i];
}
}
public:
int findTargetSumWays(vector<int>& nums, int target) {
int SUM=0;
for(int i=0;i<nums.size();i++)
{
SUM+=nums[i];
}
//计算原数组的元素之和-target后的数
//检查原数组中是否存在集合满足集合中的元素=(原数组的元素之和-target后的数)/2
//统计该类集合的个数
if((SUM-target)%2!=0)
return 0;
SUM=(SUM+target)/2;
sort(nums.begin(),nums.end());
backtracking(nums, SUM,0);
return count;
}
};特殊情况:当target=0且原数组中存在多个0时,此时不需要返回条件中的return。
三、子集问题
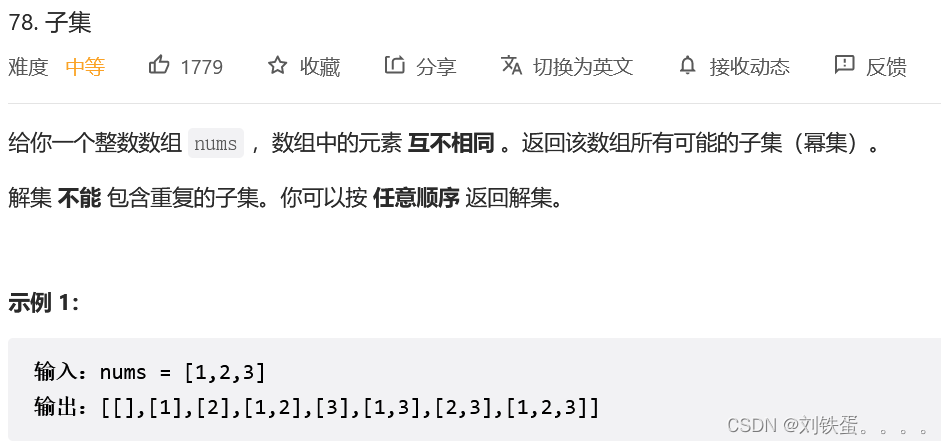
题目:78.子集
class Solution {
public:
vector<int> array;
vector<vector<int>> result;
int length=0;//用于记录结果数组中元素个数,其实也可以直接用array.size()
void backTrack(vector<int>& nums,int start)
{
//【注意:此处没有退出条件,因为他保存结果并不需要满足什么条件】
result.push_back(array);
//遍历当前层
for(int i=start;i<nums.size();i++)
{
array.push_back(nums[i]);
length++;
//递归,,为避免多层之间贡献相同索引元素,采用startIndex=i+1
backTrack(nums,i+1);
//回溯: 撤回当前层操作
array.pop_back();
length--;
}
}
vector<vector<int>> subsets(vector<int>& nums) {
int start=0;
backTrack(nums,start);
return result;
}
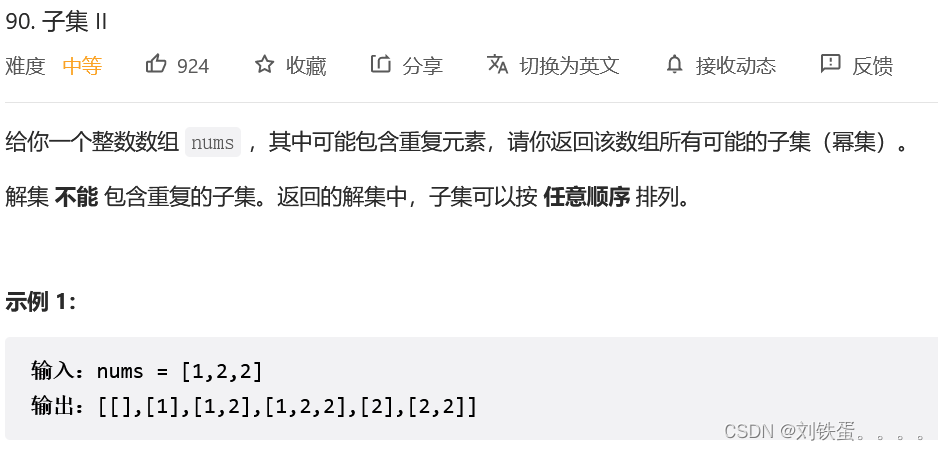
};题目:90.子集||
class Solution {
public:
vector<int> array;
vector<vector<int>> result;
void backTrack(vector<int>& nums,int start)
{
//【注意:此处没有退出条件,因为他保存结果并不需要满足什么条件】
result.push_back(array);
for(int i=start;i<nums.size();i++)
{
//当原数组中出现相同元素,且结果求的是集合不是排列时,需要去重
//i>start表示当前层如果出现前后两元素相同,则需要跳过,避免出现以下情况:
//原:[1,2a,2b,3,4] 结果:[1,2a,2] [1,2b,3]这种重复结果
if(i>start&&nums[i]==nums[i-1])
continue;//注意此处时continue不是break!!!!
array.push_back(nums[i]);
//递归,,为避免多层之间贡献相同索引元素,采用startIndex=i+1
backTrack(nums,i+1);
array.pop_back();
}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
int start=0;
//【注意,类似于求集合或者组合的题目,当需要同层去重时,则需要保证原数组是有序的】
sort(nums.begin(),nums.end());
backTrack(nums,start);
return result;
}
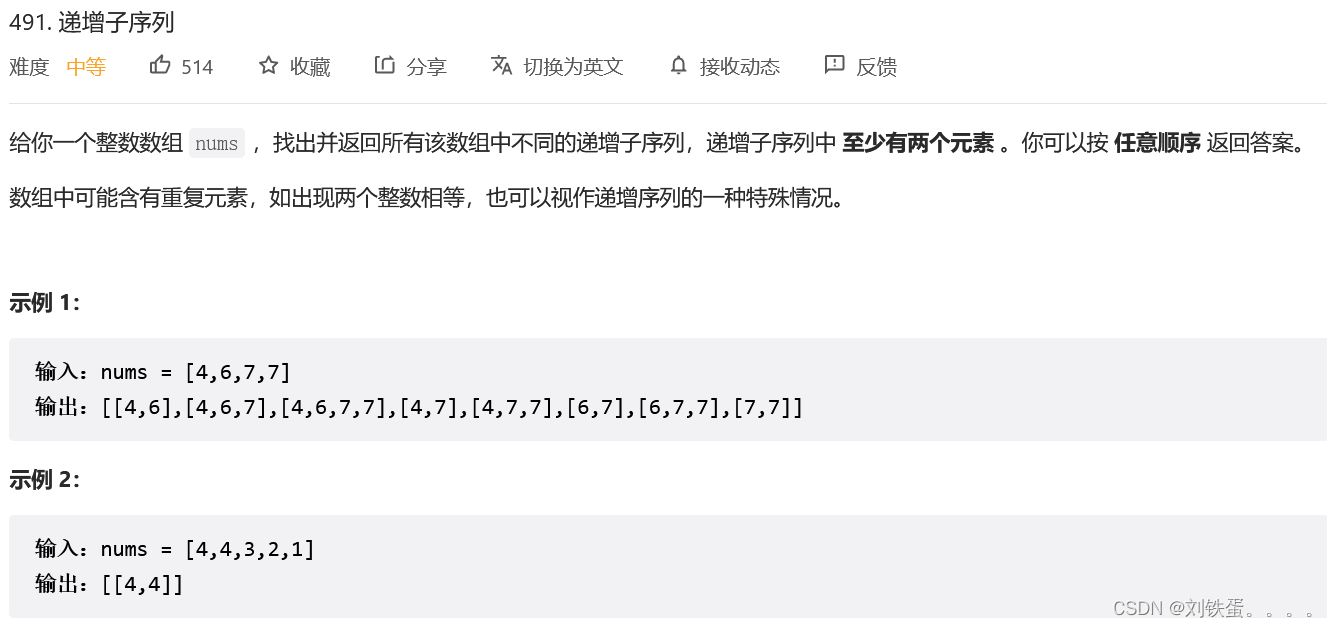
};题目:491.递增子序列
此处由于原数组是无序的,且不能将其排序,则同层去重只能使用局部unordered_set。
class Solution {
public:
vector<int> array;
vector<vector<int>> result;
void backTrack(vector<int>& nums,int start)
{
//【注意:此处没有退出条件,只要满足收集结果数组中的元素个数>1&&<nums.size()就将其压入result数组中】
if(array.size()>1&&array.size()<=nums.size())
result.push_back(array);
unordered_set<int> set;
for(int i=start;i<nums.size();i++)
{
//注意!!!,此处的同层去重不是用
//if(i-start>0&&nums[i]==nums[i-1])
//continue;
//【因为原数组并不是有序数组,同层中重复的元素并不一定是相邻,可以采用哈希表去重】
if(set.find(nums[i])!=set.end())
continue;
else
set.insert(nums[i]);
//判断当前层的该元素是否可以压入结果收集数组中,如果不行则continue,遍历下一个元素
if(array.size()==0||nums[i]>=array[array.size()-1])
array.push_back(nums[i]);
else
continue;
//递归,,为避免多层之间贡献相同索引元素,采用startIndex=i+1
backTrack(nums,i+1);
array.pop_back();
}
}
vector<vector<int>> findSubsequences(vector<int>& nums) {
int start=0;
backTrack(nums,start);
return result;
}
};四、分割问题
题目:131.分割回文串
class Solution {
private:
vector<string> array;
vector<vector<string>> result;
int length=0;
public:
//判断字符串s是否为回文字符串
bool isValid(string s)
{
int start=0;
int end=s.length()-1;
while(start<=end)
{
if(s[start]==s[end])
{
start++;
end--;
}
else
return false;
}
return true;
}
//回溯算法
void backTrack(string s,int start)
{
//当临时数组array中保存的字符串总长度等于s时,将该数组保存入结果数组中
if(length==s.length())
{
result.push_back(array);
return;
}
//每层依次截取短的回文字符串存入临时数组array中
for(int i=start;i<s.length();i++)
{
//【注意:分割使用的是截取字符串长度的方式获取每一层的贡献】
string temp(s.begin()+start,s.begin()+i+1);
if(isValid(temp))
{
array.push_back(temp);
length+=temp.size();
}
else
continue;
//递归:为了避免多层重复分割同一元素,所以采用startIndex=i+1
backTrack(s, i+1);
//回溯,撤回当前层的操作
array.pop_back();
length-=temp.size();
}
}
vector<vector<string>> partition(string s) {
int start=0;
backTrack(s, start);
return result;
}
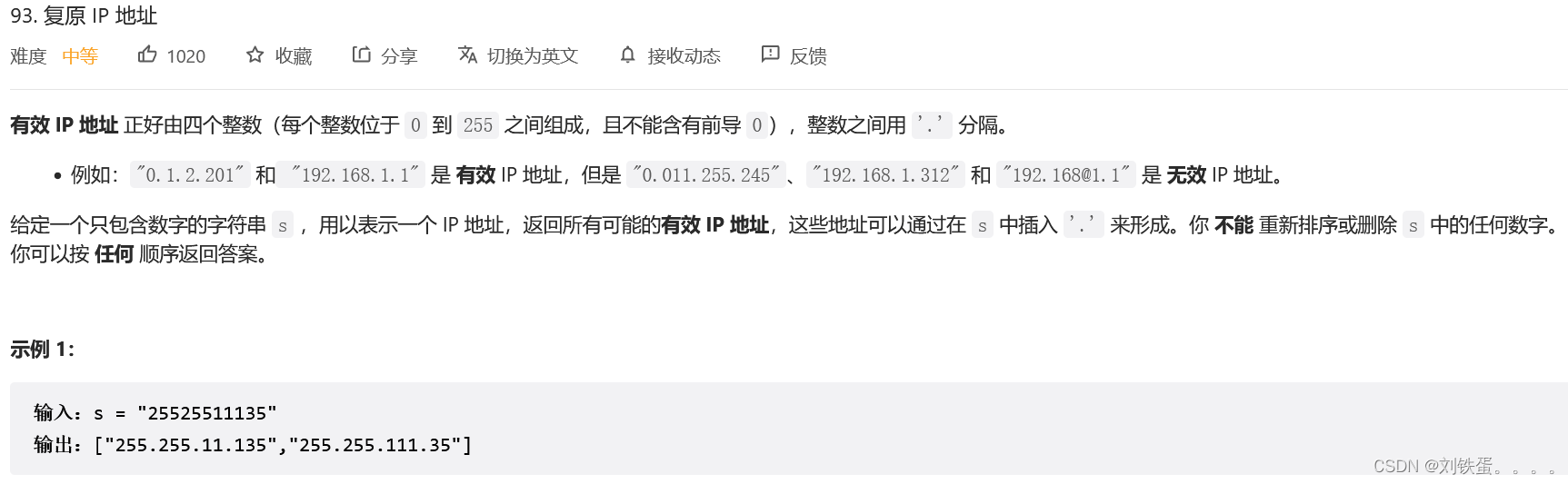
};题目:93.复原IP地址
class Solution {
public:
//字符串转整数
int ston(string s)
{
int result=0;
for(int i=0;i<s.length();i++)
{
result=10*(result+(s[i]-'0'));
}
return result/10;
}
//判断当前层的元素是否满足要求
bool valid(string s)
{
if(s.length()>1&&s[0]=='0')
return false;
if(ston(s)>255)
return false;
if(s.size()<1)
return false;
return true;
}
vector<string> result;
vector<string> array;
int length=0;
//回溯
void backTrack(string s,int start)
{
//退出条件:结果数组中元素个数不能超过四个,超过退出
if(array.size()>4)
return;
//当结果数组中元素个数小于4时,不能将所有ip都用完
if(array.size()<4&&length>=s.length())
return;
//当结果数组元素个数=4,且刚好用完所有ip,则保存该结果数组
if(array.size()==4&&length==s.length())
{
string temp=array[0];
for(int j=1;j<4;j++)
{
temp+='.';
temp+=array[j];
}
result.push_back(temp);
return;
}
//遍历当前层,截取字符串
for(int i=start;i<s.length();i++)
{
//分割字符串问题,每一层的贡献是用截取字符串的方式进行的
string temp1(s.begin()+start,s.begin()+i+1);
if(valid(temp1))
{
length+=temp1.length();
array.push_back(temp1);
//递归:为了避免多层重复分割同一元素,所以采用startIndex=i+1
backTrack(s,i+1);
}
//此处需要注意:如果当前层出现不满足分割要求的情况,直接break
else
break;
//回溯:撤回当前层的操作
length-=temp1.length();
array.pop_back();
}
}
vector<string> restoreIpAddresses(string s) {
int start=0;
backTrack(s,start);
return result;
}
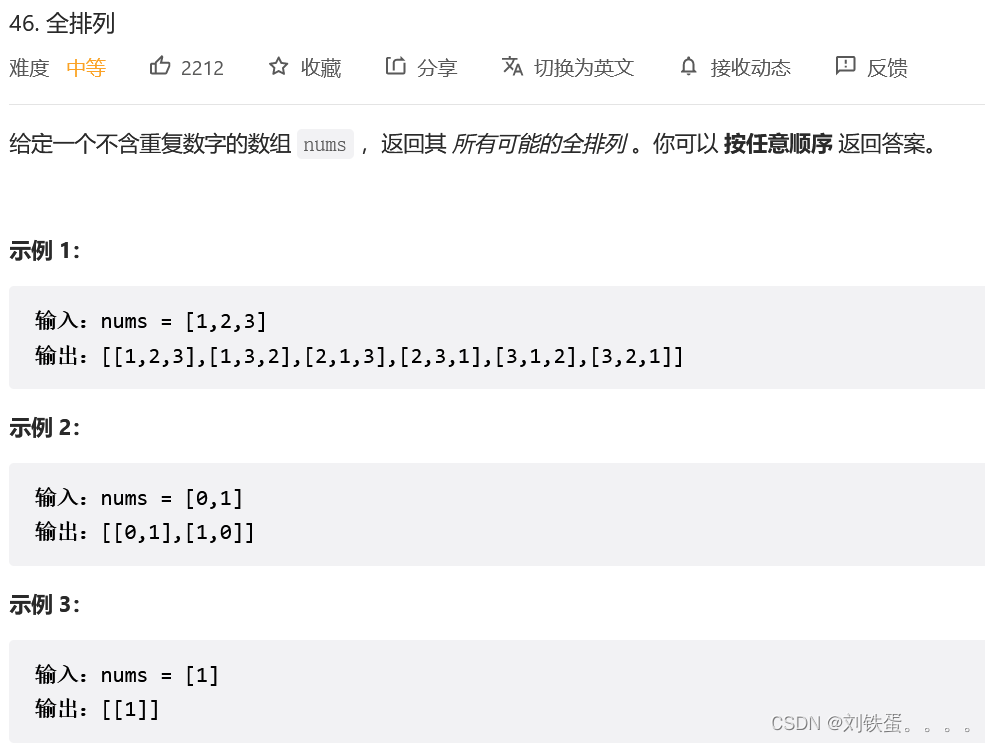
};五、排列问题
题目:46.全排列
class Solution {
public:
vector<int> array;
vector<vector<int>> result;
unordered_set<int> set;
void backTrack(vector<int>& nums)
{
//退出条件:当收集结果的数组元素个数于原数组的元素个数相同时,保存结果,退出
if(array.size()==nums.size())
{
result.push_back(array);
return;
}
//因为是全排列,所以每层都是从索引0开始索引
for(int i=0;i<nums.size();i++)
{
if(set.find(nums[i])!=set.end())
continue;
//为了多层之间贡献相同的元素,则需要用一个全局哈希表进行去重服务
set.insert(nums[i]);
array.push_back(nums[i]);
//递归
backTrack(nums);
//回溯,撤销当前层的操作
set.erase(nums[i]);
array.pop_back();
}
}
vector<vector<int>> permute(vector<int>& nums) {
backTrack(nums);
return result;
}
};题目:47.全排列||
注意:由于原数组中每个元素可能是重复的,因此为了避免不同层对同一元素进行多次获取,无法使用元素作为哈希键,此处采用数组索引作为全局哈希的键。确保不同层之间不会对同一元素多次获取。
每一层采用一个局部哈希,放置同一层中多次取同一元素,此时局部哈希只关心元素的值是否被多次重复获取,所以局部哈希的键为元素的值。
//用两个哈希表来去重
//一个全局哈希:用于保证同一结果数组中,各层贡献的元素在数组中的索引不重合;
//一个局部哈希:用于保证每一层中遍历使用的元素数值不重合;
class Solution {
public:
vector<int> array;
vector<vector<int>> result;
//全局哈希
unordered_set<int> set;
void backTrack(vector<int>& nums)
{
if(array.size()==nums.size())
{
result.push_back(array);
return;
}
//局部哈希
unordered_set<int> eset;
for(int i=0;i<nums.size();i++)
{
//局部哈希,报当前节点值相同的元素在当前层是第一次用
if(eset.find(nums[i])!=eset.end())
continue;
//全局哈希,用于确保正在收集的结果的数组中没有当前正在处理的数组序号元素
if(set.find(i)!=set.end())
continue;
eset.insert(nums[i]);
set.insert(i);
array.push_back(nums[i]);
//递归
backTrack(nums);
//回溯,撤回当前层操作
set.erase(i);
array.pop_back();
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
backTrack(nums);
return result;
}
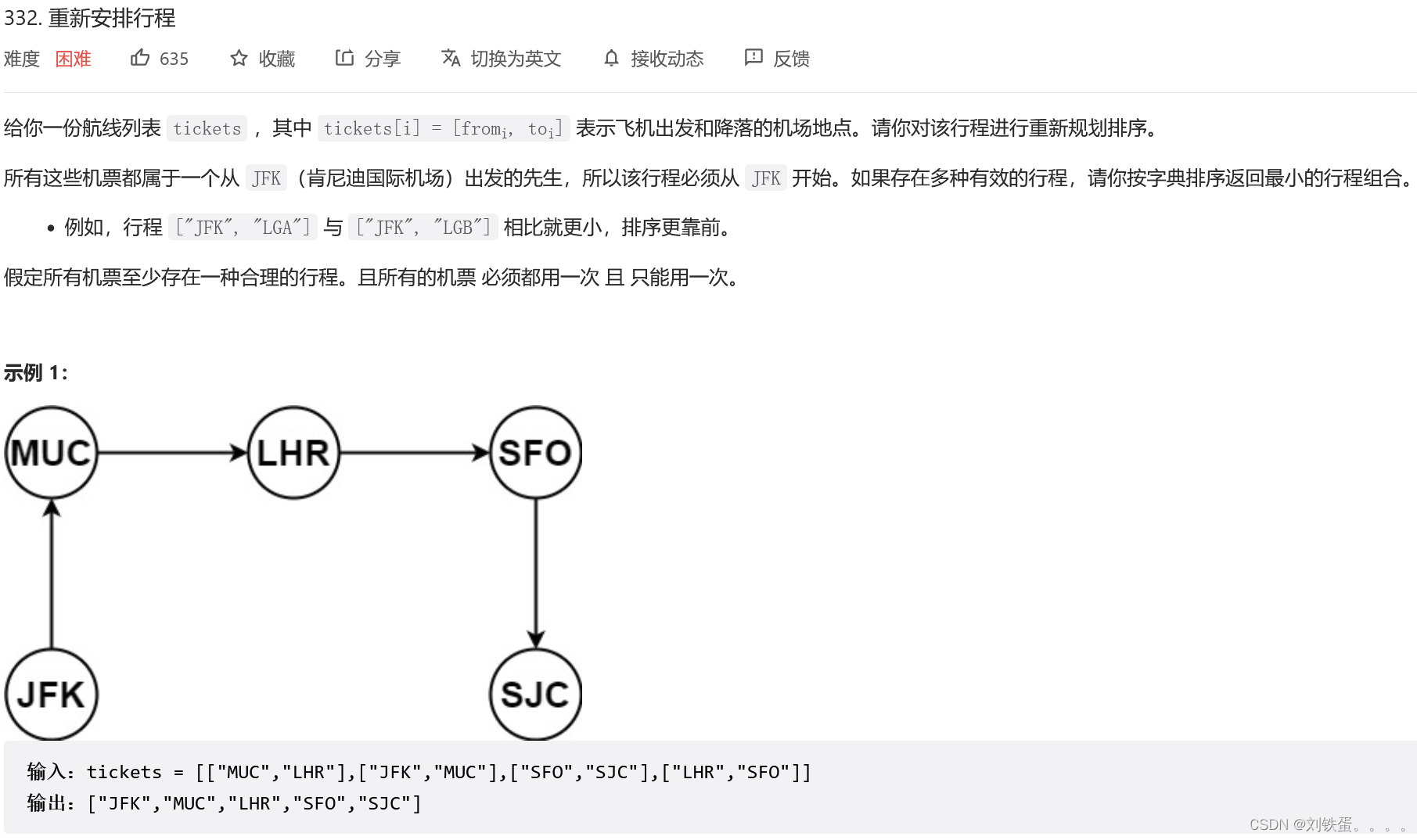
};六、行程问题
题目:332.重新安排行程问题
class Solution {
public:
int count=0;
vector<string> array;
unordered_set<int> set;
bool backTrack(vector<vector<string>>& tickets)
{
//退出条件:当所有的票都用完则退出
if(count==tickets.size())
return true;
//循环遍历,因为并不确定每一张票后面接哪张票,因此每次循环遍历都要从i=0开始
for(int i=0;i<tickets.size();i++)
{
//保证行程是以‘JFK’为起始
if(array.size()==0)
{
array.push_back("JFK");
}
//使用哈希表,避免同一张票在多层中重复使用
if(set.find(i)!=set.end())
continue;
//遍历到可以接上上张票的目的地的车票这压入结果数组中,否则继续遍历下一张票
if(tickets[i][0]==array[array.size()-1])
{
array.push_back(tickets[i][1]);
set.insert(i);
count++;
}
else
continue;
if(backTrack(tickets)) return true;
//回溯,撤回当前层操作
set.erase(i);
count--;
array.pop_back();
}
return false;
}
vector<string> findItinerary(vector<vector<string>>& tickets) {
sort(tickets.begin(),tickets.end());
backTrack(tickets);
return array;
}
};七、棋盘问题
题目:51.N皇后
//该题步骤:
//1.写出判断落子处是否合理的函数,方便回溯时直接调用
//2.使用正常回溯写就行
//有两点注意,详见题中注释
class Solution {
public:
unordered_set<int> set;
vector<string> array;
vector<vector<string>> result;
int row=0;
bool isValid(int n,int row, int col)
{
//判断该列之前是否存在皇后直接中哈希表来判断
//对同一行中的皇后不进行判断,因为每一行一旦落子1个皇后以后,就直接跳到下一行
if(set.find(col)!=set.end())
return false;
//左上角斜线【注意一:】i>=0&&j>=0条件要用&&符号,必须同时满足
for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--)
{
if(array[i][j]=='Q')
return false;
}
//右上角斜线
for(int i=row-1,j=col+1;i>=0&&j<n;i--,j++)
{
if(array[i][j]=='Q')
return false;
}
return true;
}
void backTrack(int n)
{
//退出条件:收集结果的数组大小等于n
if(array.size()==n)
{
result.push_back(array);
return;
}
//由于每一行的落子列数并无顺序,因此每行遍历都是从i=0开始
for(int j=0;j<n;j++)
{
//【注意二:】这个临时字符串必须放到这for循环的里面,放到外面会造成循环过程中temp[i]被多次赋值
string temp(n,'.');
if(isValid(n,row, j))
{
temp[j]='Q';
row++;//行++
set.insert(j);//使用过的列的哈希
array.push_back(temp);
}
else
continue;
backTrack(n);
//回溯,撤回当前层操作
row--;
set.erase(j);
array.pop_back();
}
}
vector<vector<string>> solveNQueens(int n) {
backTrack(n);
return result;
}
};题目:37.解数独
//解数独步骤
//1.写出一个判断当前落子是否有效的函数,方便回溯调用
//2.按照正常回溯写法就行
//退出条件需要注意,此处的退出条件并不是在回溯函数的开头,而是在判断当前点需要填数,但是找不到合适的数时才retrun false,或者在遍历完整个二维数组后直接return true
class Solution {
private:
int n=0;
vector<char> array={'0','1','2','3','4','5','6','7','8','9'};
public:
//判断当前空格填数n是否可行
bool isValid(int row,int col,char n,vector<vector<char>>& board)
{
for(int i=0;i<9;i++)
{
if(board[row][i]==n)
return false;
}
for(int i=0;i<9;i++)
{
if(board[i][col]==n)
return false;
}
for(int i=row/3*3;i-row/3*3<3;i++)
{
for(int j=col/3*3;j-col/3*3<3;j++)
{
if(board[i][j]==n)
return false;
}
}
return true;
}
bool backTrack(vector<vector<char>>& board)
{
//双层循环定位到当前需要填写的数字的空格
for(int i=0;i<9;i++)
{
for(int j=0;j<9;j++)
{
if(board[i][j]=='.')
{
//当前空格需要填数,遍历合适的数字填入
for(int k=1;k<=9;k++)
{
if(isValid(i,j,array[k],board))
{
//填入合适的数
board[i][j]=array[k];
//递归
if(backTrack(board))return true;
//回溯
board[i][j]='.';
}
}
return false;//【注意:本题的退出条件在此-->当前点需要填数,但是找不到合适的数】
}
}
}
return true;// 【注意:本题的退出条件在此】遍历完没有返回false,说明找到了合适棋盘位置了
}
void solveSudoku(vector<vector<char>>& board) {
backTrack(board);
}
};退出条件需要注意,此处的退出条件并不是在回溯函数的开头,而是在判断当前点需要填数,但是找不到合适的数时才retrun false,或者在遍历完整个二维数组后直接return true。