图像降噪算法——中值滤波/均值滤波/高斯滤波/双边滤波

图像降噪算法——中值滤波/均值滤波/高斯滤波/双边滤波

图像降噪算法——中值滤波/均值滤波/高斯滤波/双边滤波

空间域滤波器是最传统最简单的一类图像降噪算法，简单到我都有点不太想做写这篇博客（傲娇了…），但是为了内容的完整性，我还是在此总结下，空间域滤波器可以分为局部滤波器和非局部滤波器，其中局部滤波器又分为线性滤波器和非线性滤波器。本博客介绍几种比较经典的局部滤波器：中值滤波、均值滤波、高斯滤波、双边滤波。其中均值滤波和高斯滤波为线性滤波器，中值滤波和双边滤波为非线性滤波。

1. 基本原理

因为这些滤波器原理相对都比较简单，因为以我的理解简单描述下：
(1) 中值滤波
以目标像素周围 $3\times3$ 的邻域为例，就是将 $3\times3$ 邻域中九个像素灰度值进行排序，将中间灰度值作为目标像素的灰度值。椒盐噪声影响的像素的灰度值通常都非常大或者非常小，因此通过排序会被消除掉。

(2) 均值滤波
同样以目标像素周围 $3\times3$ 的邻域为例，就是将 $3\times3$ 邻域中九个像素灰度值的平均值作为目标像素的灰度值

(3) 高斯滤波
高斯滤波就是将均值滤波中的平局值改为高斯加权平均值，邻域中年距离目标像素越远的像素灰度值权重越小，通常通过生成一个高斯模板实现

(4) 双边滤波
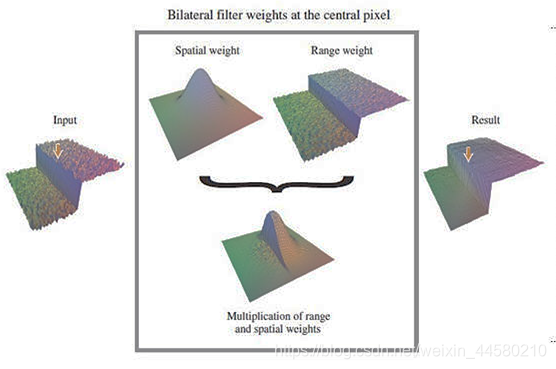
双边滤波是在高斯滤波的基础上在权重设计中进一步考虑了像素灰度梯度的影响，首先考虑高斯部分权重（下图中的Spatial weight）： $w_{d}(i, j, k, l)=\exp \left(-\frac{(i-k)^{2}+(j-l)^{2}}{2 \sigma_{d}^{2}}\right)$ 然后考虑像素灰度梯度部分权重（下图中的Range weight）： $w_{r}(i, j, k, l)=\exp \left(-\frac{\|f(i, j)-f(k, l)\|^{2}}{2 \sigma_{r}^{2}}\right)$ 其中 $(i, j)$ 为模板中邻域像素坐标， $(i, j)$ 为模板中心像素坐标， $f (i, j)$ 为坐标 $(i, j)$ 处的像素值， $\sigma_d$ 和 $\sigma_r$ 分别为两个权重的方差，将两部分权重相乘即获得双边滤波的权重： $l)=w_{d}(i, j, k, l) * w_{r}(i, j, k, l)=\exp \left(-\frac{(i-k)^{2}+(j-l)^{2}}{2 \sigma_{d}^{2}}-\frac{\|f(i, j)-f(k, l)\|^{2}}{2 \sigma_{r}^{2}}\right)$ 可以参看下图进行理解：

在这里插入图片描述

2. C++代码实现

下面是基于OpenCV对以上四种滤波器的实现：

Mat Denoise::MedeanFilter(const Mat &src, int size)
{
    Mat dst = src.clone();
    int start = size/2;
    for(int i = start; i < dst.rows-start; i++)
    {
        for(int j = start; j < dst.cols-start; j++)
        {
            vector<uchar> model;
            for(int m = i-start; m <= i+start; m++)
            {
                for(int n = j-start; n <= j+start; n++)
                {
                    model.push_back(src.at<uchar>(m,n));
                }
            }
            sort(model.begin(), model.end());
            dst.at<uchar>(i,j) = model[size*size/2];
        }
    }
    return dst;
}

//均值滤波
Mat Denoise::MeanFilter(const Mat &src, int size)
{
    Mat dst = src.clone();
    int start = size/2;
    for(int i = start; i < dst.rows-start; i++)
    {
        for(int j = start; j < dst.cols-start; j++)
        {
            int sum = 0;
            for(int m = i-start; m <= i+start; m++)
            {
                for(int n = j-start; n <= j+start; n++)
                {
                   sum += src.at<uchar>(m,n);
                }
            }
            dst.at<uchar>(i,j) = (uchar)(sum/size/size);
        }
    }
    return dst;
}

//高斯滤波
Mat Denoise::GaussianFilter(const Mat &src, int size, double sigma)
{
    vector<vector<double>> gaussianTemplate = GaussianTemplate(size, sigma);
    Mat dst = src.clone();
    int start = size/2;
    for(int i = start; i < dst.rows-start; i++)
    {
        for(int j = start; j < dst.cols-start; j++)
        {
            int sum = 0;
            for(int m = i-start; m <= i+start; m++)
            {
                for(int n = j-start; n <= j+start; n++)
                {
                    sum += src.at<uchar>(m,n)*gaussianTemplate[m-i+start][n-j+start];
                }
            }
            dst.at<uchar>(i,j) = (uchar)sum;
        }
    }
    return dst;
}

vector<vector<double>> Denoise::GaussianTemplate(int size, double sigma)
{
    vector<vector<double>> temp;
    double base = 1.0 / 2.0 / CV_PI / sigma / sigma;
    for(int i = 0; i < size; i++)
    {
        vector<double> vec;
        for(int j = 0; j < size; j++)
        {
            double a = (pow(i - size/2, 2) + pow(j - size/2, 2)) / 2.0 / sigma / sigma;
            double b = base * exp(-a);
            vec.push_back(b);
        }
        temp.push_back(vec);
    }
    return temp；
}

//双边滤波
Mat Denoise::BilateralFilter(const Mat &src, int size, double sigmaD, double sigmaR)
{
    vector<vector<double>> tempD;
    vector<double> tempR;
    Mat dst = src.clone();

    //生成定义域模板
    for(int i = 0; i < size; i++)
    {
        vector<double> vec;
        for(int j = 0; j < size; j++)
        {
            double a = (pow(i - size/2, 2) + pow(j - size/2, 2)) / 2.0 / sigmaD / sigmaD;
            double b = exp(-a);
            vec.push_back(b);
        }
        tempD.push_back(vec);
    }

    //生成值域模板
    for(int i = 0; i < 256; i++)
    {
        double a = (i * i / 2.0 / sigmaR / sigmaR);
        double b = exp(-a);
        tempR.push_back(b);
    }

    int start = size/2;
    for(int i = start; i < dst.rows-start; i++)
    {
        for(int j = start; j < dst.cols-start; j++)
        {
            double sum = 0;
            double weightSum = 0;
            for(int m = i-start; m <= i+start; m++)
            {
                for(int n = j-start; n <= j+start; n++)
                {
                    double weight = tempD[m-i+start][n-j+start] * tempR[abs(src.at<uchar>(m,n)-src.at<uchar>(i,j))];
                    sum += src.at<uchar>(m,n)*weight;
                    weightSum += weight;
                }
            }
            dst.at<uchar>(i,j) = (uchar)sum/weightSum;
        }
    }
    return dst;
}

运行结果如下：
首先，原图如下图所示：在这里插入图片描述
我们首先看看中值滤波对椒盐噪声的效果:
添加椒盐噪声后图像如下：

中值滤波后效果如下：

然后我们来对比下均值滤波、高斯滤波和双边滤波对高斯噪声的效果：
添加高斯噪声的图像如下：在这里插入图片描述
均值滤波后效果如下：

高斯滤波后效果如下：

双边滤波效果如下：