双目深度算法——基于Cost Volume的方法(GC-Net / PSM-Net / GA-Net)
双目深度算法——基于Cost Volume的方法(GC-Net / PSM-Net / GA-Net)
在之前的工作中有接触过Stereo Depth这个方向,在读书期间也有用过ZED这样的传感器,但是一直没有对这个方向进行过系统的学习,因此我打算这段时间花点时间学习下这方面的知识,之前有写过一篇相关的文档双目视觉深度——SGM中的动态规划,SGM主要思想是基于动态优化,NN发展后逐渐衍生出了基于Feature进行Match的方法,再后来就是基于Correlation和Cost Volume方法的提出,以及最近这两年比较火的基于Transformer的方法。
本篇博客主要介绍以Cost Volume为基础的相关网络框架。以GC-Net为例搞清楚什么是Cost Volume,然后根据介绍两篇基于GC-Net优化的网络。
1. GC-Net
GC-Net发表于2017年CVPR,原论文名为《End-to-End Learning of Geometry and Context for Deep Stereo Regression》,是最开始提出Cost Volume的方法之一
1.1 网络结构及损失函数
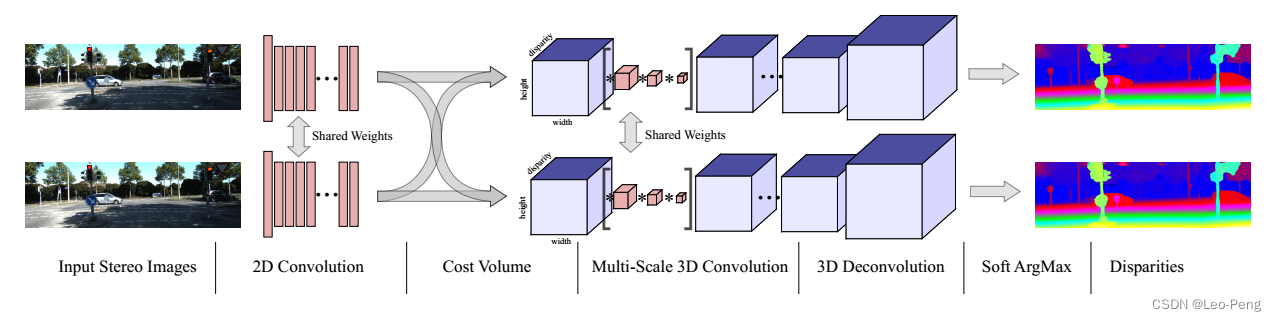
GC-Net网络结构如下图所示:
具体的参数如下表:
网络主要分为三部分:用于提取Feature的2D卷积、Cost Volume的构造以及3D卷积,下面我们结合代码来开拿下具体是如何实现的(代码参考的是zyf12389/GC-Net,因为是复现的代码,代码实现和原论文可能稍微有些细微差别):
特征提取部分第一层首先对输入图片 H × W × 3 H\times W\times 3 H×W×3进行一个下采样,然后接了一个ResNet的Backbone,从ResNet输出的特征大小为 H 2 × W 2 × F \frac{H}{2}\times \frac{W}{2} \times F 2H×2W×F,代码如下:
imgl0=F.relu(self.bn0(self.conv0(imgLeft)))
imgr0=F.relu(self.bn0(self.conv0(imgRight)))
imgl_block=self.res_block(imgl0)
imgr_block=self.res_block(imgr0)
imgl1=self.conv1(imgl_block)
imgr1=self.conv1(imgr_block)
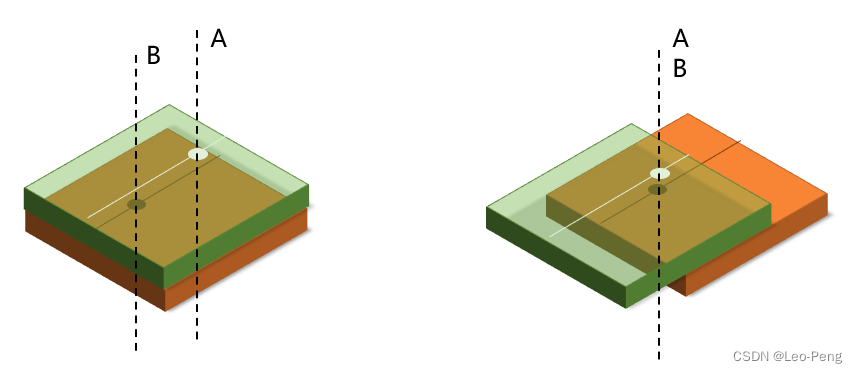
然后就是利用特征构建Cost Volume,构建Cost Volume的目的是为了将视差这一概念表达在网络结构中,这其实很好理解,如下图所示,如果我们仅仅将两张图的图像特征简单地叠到一起,网络怎么知道A处和B处有特征有对应关系呢,可想而知是很困难的,而我们如果能够根据视差将A处和B处的的特征进行对齐,然后再进行卷积,网络学习到A处和B处的对应关系就会简单很多,而Cost Volume就是将所有可能的视差遍历一遍,让网络更容易学习到不同视差下的特征的对应关系:
Cost Volume部分的代码如下:
cost_volum = self.cost_volume(imgl1,imgr1)
def cost_volume(self,imgl,imgr):
xx_list = []
pad_opr1 = nn.ZeroPad2d((0, self.maxdisp, 0, 0))
xleft = pad_opr1(imgl)
for d in range(self.maxdisp): # maxdisp+1 ?
pad_opr2 = nn.ZeroPad2d((d, self.maxdisp - d, 0, 0))
xright = pad_opr2(imgr)
xx_temp = torch.cat((xleft, xright), 1)
xx_list.append(xx_temp)
xx = torch.cat(xx_list, 1)
xx = xx.view(self.batch, self.maxdisp, 64, int(self.height / 2), int(self.width / 2) + self.maxdisp)
xx0=xx.permute(0,2,1,3,4)
xx0 = xx0[:, :, :, :, :int(self.width / 2)]
return xx0
我们可以看到实际的构建流程是:
(1)先利用ZeroPad2d将左图特征从
H
2
×
W
2
×
D
\frac{H}{2}\times \frac{W}{2} \times D
2H×2W×D大小填充为
H
2
×
(
W
2
+
M
)
×
D
\frac{H}{2}\times (\frac{W}{2} +M) \times D
2H×(2W+M)×D大小,其中
D
D
D为入参定义的最大视差;
(2)然后将右图特征也填充为
H
2
×
(
W
2
+
M
)
×
F
\frac{H}{2}\times (\frac{W}{2} +M) \times F
2H×(2W+M)×F大小,与左图特征不同的是,左图特征是将填充集中在原始特征的右侧,而右图则是按照视差从小达到的变化逐渐调整原始特征左右的填充列数;
(3)接着将左右特征按行方向Concat到一起;
(4)最后拼接成的特征图调整为
D
×
2
F
×
H
2
×
W
2
D \times 2F \times \frac{H}{2}\times \frac{W}{2}
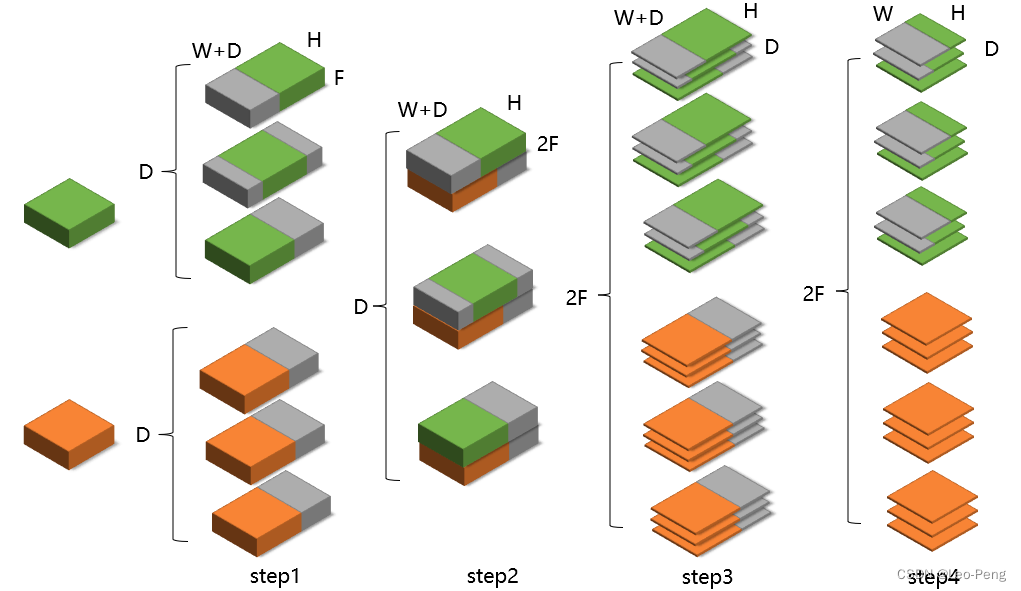
D×2F×2H×2W大小,具体流程如下图所示:
绿色和橙色分别表示左图和右图的图像feature,灰色代表zero padding的部分,由于我参考的代码是复现代码,我担心复现的老哥写的代码有Bug,因此我又参考了PSM-Net的官方实现,如下所示:
cost = Variable(torch.FloatTensor(refimg_fea.size()[0], refimg_fea.size()[1]*2, self.maxdisp/4, refimg_fea.size()[2], refimg_fea.size()[3]).zero_(), volatile= not self.training).cuda()
for i in range(self.maxdisp/4):
if i > 0 :
cost[:, :refimg_fea.size()[1], i, :,i:] = refimg_fea[:,:,:,i:]
cost[:, refimg_fea.size()[1]:, i, :,i:] = targetimg_fea[:,:,:,:-i]
else:
cost[:, :refimg_fea.size()[1], i, :,:] = refimg_fea
cost[:, refimg_fea.size()[1]:, i, :,:] = targetimg_fea
cost = cost.contiguous()
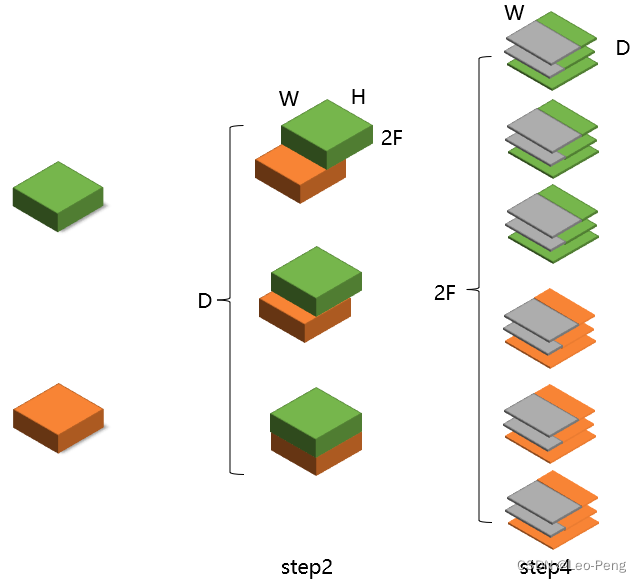
仔细对比可以发现其实构建的Cost Volume是大同小异的,如下图所示:
区别是,PSM-Net官方代码构建的Cost Volume中“橙色”特征在没有和“绿色”特征重合部分填充的是0,而GC-Net复现代码中“橙色”特征保留的是原始的图像特征,以我以往的经验来说,这种区别应该对最终结构的影响不大。
通过上述Cost Volume,我们得到的是 2 F 2F 2F个 D × H 2 × W 2 D \times \frac{H}{2}\times \frac{W}{2} D×2H×2W大小的3D特征图,紧接着我们就是在上述3D特征图进行3D卷积,如下所示:
conv3d_out=F.relu(self.bn3d_1(self.conv3d_1(cost_volum)))
conv3d_out=F.relu(self.bn3d_2(self.conv3d_2(conv3d_out)))
conv3d_block_1=self.block_3d_1(cost_volum)
conv3d_21=F.relu(self.bn3d_3(self.conv3d_3(cost_volum)))
conv3d_block_2=self.block_3d_2(conv3d_21)
conv3d_24=F.relu(self.bn3d_4(self.conv3d_4(conv3d_21)))
conv3d_block_3=self.block_3d_3(conv3d_24)
conv3d_27=F.relu(self.bn3d_5(self.conv3d_5(conv3d_24)))
conv3d_block_4=self.block_3d_4(conv3d_27)
deconv3d=F.relu(self.debn1(self.deconv1(conv3d_block_4))+conv3d_block_3)
deconv3d=F.relu(self.debn2(self.deconv2(deconv3d))+conv3d_block_2)
deconv3d=F.relu(self.debn3(self.deconv3(deconv3d))+conv3d_block_1)
deconv3d=F.relu(self.debn4(self.deconv4(deconv3d))+conv3d_out)
为了减小计算量,3D卷积的过程是一个类似U-Net的结构,先对特征图进行Down Sample,然后通过再通过转置卷积进行Up Sample,对于转置卷积不了解的同学可以参考下计算机视觉算法——图像分割网络总结,其中我对2D转置卷积的原理和计算过程进行了详细的分析,这里就不再赘述(其中ConvTranspose3d的output_padding设置为1是为了保证输入输出特征图大小一致)。
最后就是从输出特征中获取视差,论文中还特地提到了他们建立的是一种Soft Argmin获取视差,3D卷积最后的输出特征图大小为 D × H × W D \times {H}\times {W} D×H×W,我们很直接想到的一种方式是在输出特征的视差维度上取Argmin或者Argmax,但是论文中提到,这种方式无法获得亚像素级的视差以且不可微,因此论文通过Soft Argmin获取视差,其实就是在视差维度进行Softmax后然后进行加权平均: s o f t _ a r g m a x = Σ d = 0 D m a x d × σ ( − c d ) soft\_argmax=\Sigma^{D_{max}}_{d=0}d\times\sigma(-c_d) soft_argmax=Σd=0Dmaxd×σ(−cd)其中, d d d为视差, σ \sigma σ为Softmax操作, c d c_d cd为输出的特征,具体代码如下:
loss_mul_list = []
for d in range(maxdisp):
loss_mul_temp = Variable(torch.Tensor(np.ones([batch, 1, h, w]) * d)).cuda()
loss_mul_list.append(loss_mul_temp)
loss_mul = torch.cat(loss_mul_list, 1)
x = net(left_image, right_image)
result = torch.sum(x.mul(loss_mul), 1)
获得视差后最后构建 L 1 L1 L1损失,至此就完成了整个网络结构的介绍。
2. PSM-Net
PSM-Net原论文名为《Pyramid Stereo Matching Network》,发表于2018年,PSM-Net的网络Pipeline和和GC-Net的几乎一致,只是在特征提取的BackBone和3D卷积部分使用了特殊结构,使得网络具备更大的感受野,从而在一些细节上能取得更好的效果,如下所示:
在计算速度上,PSM-Net也要优于GC-Net
2.1 网络结构及损失函数
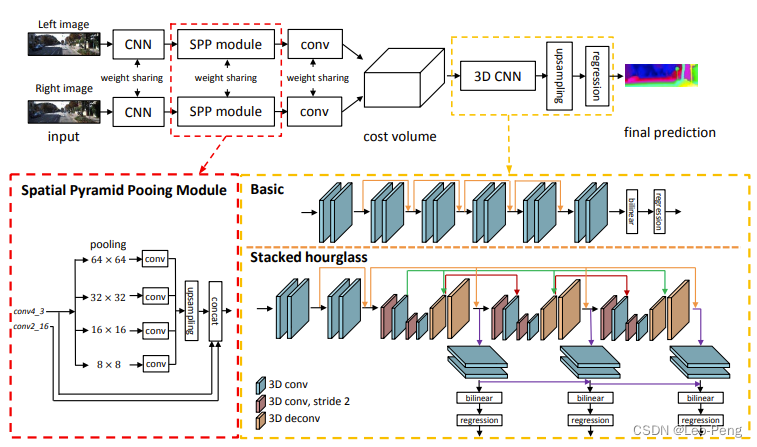
PSM-Net网络结构如下图所示:
从上图中可以看出,在特征提取部分,PSM-Net将原本的ResNet更换为了SPP Modlue,在3D卷积部分,PSM-Net将原本类似U-Net的网络结构更换为了Stacked Hourglass结构,除此之外,在Loss方面,PSM-Net将原本的L1 Loss更换为了Smooth L1 Loss,公式如下:
L
(
d
,
d
^
)
=
1
N
∑
i
=
1
N
smooth
L
1
(
d
i
−
d
^
i
)
L(d, \hat{d})=\frac{1}{N} \sum_{i=1}^{N} \operatorname{smooth}_{L_{1}}\left(d_{i}-\hat{d}_{i}\right)
L(d,d^)=N1i=1∑NsmoothL1(di−d^i)其中
smooth
L
1
(
x
)
=
{
0.5
x
2
,
if
∣
x
∣
<
1
∣
x
∣
−
0.5
,
otherwise
\text { smooth }_{L_{1}}(x)= \begin{cases}0.5 x^{2}, & \text { if }|x|<1 \\ |x|-0.5, & \text { otherwise }\end{cases}
smooth L1(x)={0.5x2,∣x∣−0.5, if ∣x∣<1 otherwise 下面我们来复习下SPP Module和Stacked Hourglass结构
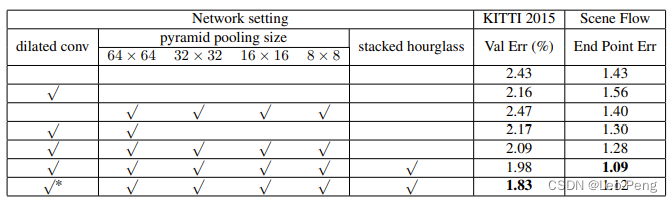
SPP Module首次提出于论文《Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition》,SPP Module的原理就是通过多路不同尺度的Pooling实现多尺度特征融合,该模块被广泛应用于各种网络中,例如在分割网络中,DeepLab V2结合膨胀卷积和SPP模块提出ASPP模块,用于解决目标多尺度的问题;在目标检测网络中,YOLO v3结合SPP模块提出了YOLO v3 SPP模型,有效提高了目标检测精度。在PSM-Net中也是如此,通过消融实验对比可以看出SPP模块还是很有的:
Stacked Hourglass首次提出于论文《Stacked Hourglass Networks for Human Pose Estimation》,该论文中原始的Stacked Hourglass结构相对复杂,但是最核心的思想就是叠加的Encoder-Decoder结构以及中继监督,在PSM-Net中也是如此,在3D卷积的部分中使用三层类似UNet的Encoder-Decoder结构,并且在每一层的输出处都进行了监督(中继监督)。
总而言之,PSM-Net在原理上相对GC-Net并没有差异,仅仅是在网络结构上使用了更加优雅的Backbone从而取得了更好的效果
3. GA-Net
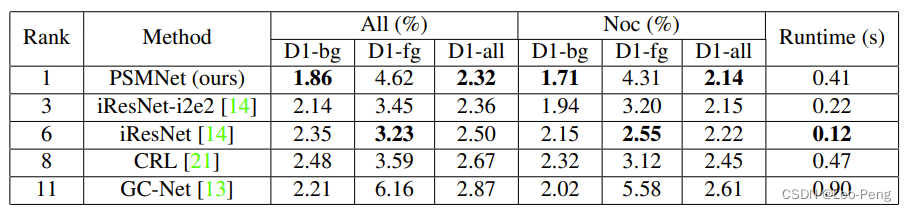
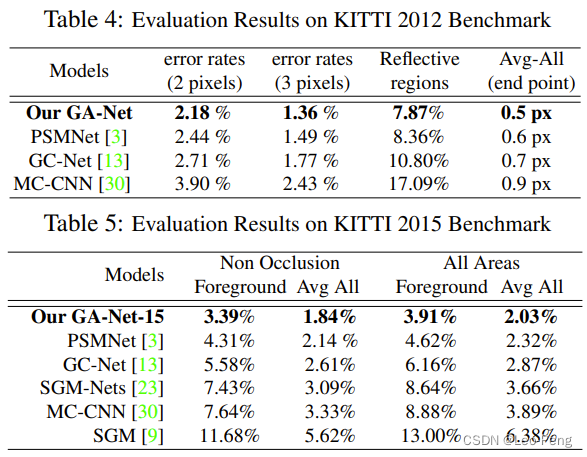
GA-Net原论文名为《GA-Net: Guided Aggregation Net for End-to-end Stereo Matching》,发表于2019年,在论文中提到,尽管PSM-Net通过优化网络结构使得计算量和显存占用相对减小,但是Encoder-Decoder这样的结构使得网路精度损失,GA-Net则是借鉴传统SGM算法中Aggregation原理设计了LGA层和SGA层来替代3D卷积以达到更好的效果。如下图所示,GA-Net相对于GC-Net和PSM-Net都有更好的效果(速度和计算量并没有太大提升)。
3.1 网络结构及损失函数
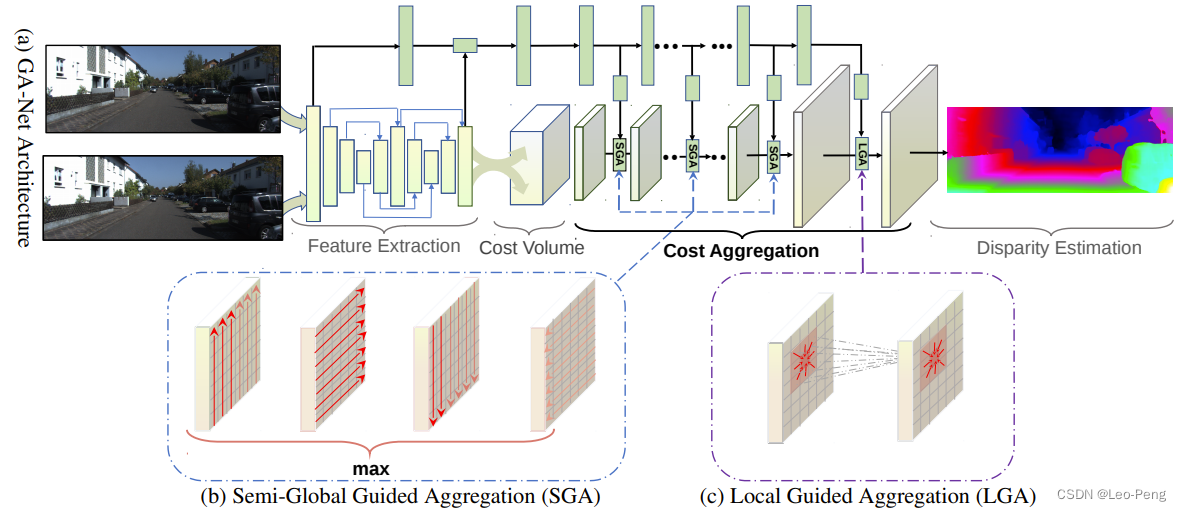
GA-Net网络结构如下图所示:
从上图中我们可以看出主要流程仍然是先提取特征,然后构建Cost Volume,再进行代价聚合,最后计算Smooth L1损失。但与之前方法主要不同的是,GA-Net通过子网络学习这个惩罚系数来进一步指导网络进行代价聚合,这就是GA-Net中Guided的由来,这部分子网络就是网络结构图中上方绿色方框部分,实际实现上就是一些2D卷积,输入是原始的RGB图像,输出是聚合过程中的惩罚系数。GA-Net在3D卷积部分加入了SGA和LGA两种代价聚合模块,下面我们主要来分析下SGA和LGA模块的原理:
SGA指的是Semi-Global Aggregation,这部分算法思路主要借鉴的是SGM算法中代价聚合原理,这部分细节读者可以参考双目视觉深度——SGM中的动态规划,在此我就不再重复,在SGM中代价聚合损失函数定义如下:
C
r
A
(
p
,
d
)
=
C
(
p
,
d
)
+
min
{
C
r
A
(
p
−
r
,
d
)
,
C
r
A
(
p
−
r
,
d
−
1
)
+
P
1
,
C
r
A
(
p
−
r
,
d
+
1
)
+
P
1
,
min
i
C
r
A
(
p
−
r
,
i
)
+
P
2
C_{\mathbf{r}}^{A}(\mathbf{p}, d)=C(\mathbf{p}, d)+\min \left\{\begin{array}{l} C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, d), \\ C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, d-1)+P_{1}, \\ C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, d+1)+P_{1}, \\ \min _{i} C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, i)+P_{2} \end{array}\right.
CrA(p,d)=C(p,d)+min⎩
⎨
⎧CrA(p−r,d),CrA(p−r,d−1)+P1,CrA(p−r,d+1)+P1,miniCrA(p−r,i)+P2该代价聚合公式在深度神经网络中是无法使用的,原因是:
(1)惩罚项
P
1
P_{1}
P1、
P
2
P_{2}
P2是超参数,在网络训练过程中是不稳定的且难调优的;
(2)公式中的阈值和惩罚项对不同的区域和像素都是固定的,这导致算法适应能力较差;
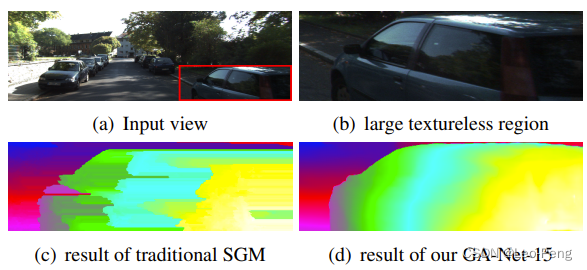
(3)硬阈值对导致估计出来的深度中存在大量的平行曲面,如下图所示:
GA-Net对此进行了改进:
C
r
A
(
p
,
d
)
=
C
(
p
,
d
)
+
sum
{
w
1
(
p
,
r
)
⋅
C
r
A
(
p
−
r
,
d
)
w
2
(
p
,
r
)
⋅
C
r
A
(
p
−
r
,
d
−
1
)
w
3
(
p
,
r
)
⋅
C
r
A
(
p
−
r
,
d
+
1
)
w
4
(
p
,
r
)
⋅
max
i
C
r
A
(
p
−
r
,
i
)
C_{\mathbf{r}}^{A}(\mathbf{p}, d)=C(\mathbf{p}, d)+\operatorname{sum}\left\{\begin{array}{l} \mathbf{w}_{1}(\mathbf{p}, \mathbf{r}) \cdot C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, d) \\ \mathbf{w}_{2}(\mathbf{p}, \mathbf{r}) \cdot C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, d-1) \\ \mathbf{w}_{3}(\mathbf{p}, \mathbf{r}) \cdot C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, d+1) \\ \mathbf{w}_{4}(\mathbf{p}, \mathbf{r}) \cdot \max _{i} C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, i) \end{array}\right.
CrA(p,d)=C(p,d)+sum⎩
⎨
⎧w1(p,r)⋅CrA(p−r,d)w2(p,r)⋅CrA(p−r,d−1)w3(p,r)⋅CrA(p−r,d+1)w4(p,r)⋅maxiCrA(p−r,i)其中
w
\mathbf{w}
w是通过子网络学习的惩罚系数/权重,
C
(
p
,
d
)
∈
R
H
×
W
×
D
max
×
F
C(p, d) \in R^{H \times W \times D_{\max \times F}}
C(p,d)∈RH×W×Dmax×F为匹配代价体,对比可以看出,与SGM的代价聚合函数不同的地方有:
(1)所有参数都是可学习的,因此增强了算法的适应能力;
(1)使用加权平均代替求原始函数最外部的求最小,保留算法精度;
(2)使用求最大代替原始函数内部的求最大,因为GA-Net中
C
(
p
,
d
)
C(\mathbf{p}, d)
C(p,d)表示的和真值的相似度,而不是原始函数的直接的损失函数。
上式由于是一个累加公式,其中第四个公式可能会导致一些非常大的异常值出现,这对网络的收敛也是不利的,因此GA-Net进一步将代价聚合公式优化为:
C
r
A
(
p
,
d
)
=
sum
{
w
0
(
p
,
r
)
⋅
C
(
p
,
d
)
w
1
(
p
,
r
)
⋅
C
r
A
(
p
−
r
,
d
)
w
2
(
p
,
r
)
⋅
C
r
A
(
p
−
r
,
d
−
1
)
w
3
(
p
,
r
)
⋅
C
r
A
(
p
−
r
,
d
+
1
)
w
4
(
p
,
r
)
⋅
max
i
C
r
A
(
p
−
r
,
i
)
C_{\mathbf{r}}^{A}(\mathbf{p}, d)=\operatorname{sum}\left\{\begin{array}{l} \mathbf{w}_{0}(\mathbf{p}, \mathbf{r}) \cdot C(\mathbf{p}, d) \\ \mathbf{w}_{1}(\mathbf{p}, \mathbf{r}) \cdot C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, d) \\ \mathbf{w}_{2}(\mathbf{p}, \mathbf{r}) \cdot C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, d-1) \\ \mathbf{w}_{3}(\mathbf{p}, \mathbf{r}) \cdot C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, d+1) \\ \mathbf{w}_{4}(\mathbf{p}, \mathbf{r}) \cdot \max _{i} C_{\mathbf{r}}^{A}(\mathbf{p}-\mathbf{r}, i) \end{array}\right.
CrA(p,d)=sum⎩
⎨
⎧w0(p,r)⋅C(p,d)w1(p,r)⋅CrA(p−r,d)w2(p,r)⋅CrA(p−r,d−1)w3(p,r)⋅CrA(p−r,d+1)w4(p,r)⋅maxiCrA(p−r,i)
s.t.
∑
i
=
0
,
1
,
2
,
3
,
4
w
i
(
p
,
r
)
=
1
\text { s.t. } \quad \sum_{i=0,1,2,3,4} \mathbf{w}_{i}(\mathbf{p}, \mathbf{r})=1
s.t. i=0,1,2,3,4∑wi(p,r)=1其中
∑
i
=
0
,
1
,
2
,
3
,
4
w
i
(
p
,
r
)
=
1
\quad \sum_{i=0,1,2,3,4} \mathbf{w}_{i}(\mathbf{p}, \mathbf{r})=1
∑i=0,1,2,3,4wi(p,r)=1对参数进行了归一化,限制了
C
(
p
,
d
)
C(\mathbf{p}, d)
C(p,d)的元素大小。为了节省计算量,SGA模块只在四个方向上进行代价聚合,即
r
∈
{
(
0
,
1
)
,
(
0
,
−
1
)
,
(
1
,
0
)
,
(
−
1
,
0
)
}
\mathbf{r} \in\{(0,1),(0,-1),(1,0),(-1,0)\}
r∈{(0,1),(0,−1),(1,0),(−1,0)},代价最后输出为四个方向代价聚合结果的最大值
C
A
(
p
,
d
)
=
max
r
C
r
A
(
p
,
d
)
C^{A}(\mathbf{p}, d)=\max _{\mathbf{r}} C_{\mathbf{r}}^{A}(\mathbf{p}, d)
CA(p,d)=rmaxCrA(p,d)在传统的SGM算法中是通过求和获得最后的代价聚合结果,而在SGA模块中通过四个方向选择最大值的这种方式可以避免其他方向的干扰,而这种方式可以通过多次叠加来后来获得更好的代价体,是一种更适合网络的方式。由于一共有四个方向,且公式中有五种权重值,因此SGA输出的权重矩阵大小为
4
×
H
×
W
×
K
×
F
(
K
=
5
)
4 \times H \times W \times K \times F(K=5)
4×H×W×K×F(K=5)。
LGA指的是Local Cost Aggregation,局部代价聚合我理解其实就是一种滤波方法,目的是使得深度图中边缘结构更加清晰,传统算法中的局部滤波公式如下: C A ( p , d ) = ∑ q ∈ N p ω ( p , q ) ⋅ C ( q , d ) C^{A}(\mathbf{p}, d)=\sum_{\mathbf{q} \in N_{\mathbf{p}}} \omega(\mathbf{p}, \mathbf{q}) \cdot C(\mathbf{q}, d) CA(p,d)=q∈Np∑ω(p,q)⋅C(q,d)对于某一点,在其领域内对各个代价加权求和,这个权重和RGB有关,在GA-Net中,该公式优化为: C A ( p , d ) = sum { ∑ q ∈ N p ω 0 ( p , q ) ⋅ C ( q , d ) ∑ q ∈ N p ω 1 ( p , q ) ⋅ C ( q , d − 1 ) , ∑ q ∈ N p ω 2 ( p , q ) ⋅ C ( q , d + 1 ) C^{A}(\mathbf{p}, d)=\operatorname{sum}\left\{\begin{array}{l} \sum_{\mathbf{q} \in N_{\mathbf{p}}} \omega_{0}(\mathbf{p}, \mathbf{q}) \cdot C(\mathbf{q}, d) \\ \sum_{\mathbf{q} \in N_{\mathbf{p}}} \omega_{1}(\mathbf{p}, \mathbf{q}) \cdot C(\mathbf{q}, d-1), \\ \sum_{\mathbf{q} \in N_{\mathbf{p}}} \omega_{2}(\mathbf{p}, \mathbf{q}) \cdot C(\mathbf{q}, d+1) \end{array}\right. CA(p,d)=sum⎩ ⎨ ⎧∑q∈Npω0(p,q)⋅C(q,d)∑q∈Npω1(p,q)⋅C(q,d−1),∑q∈Npω2(p,q)⋅C(q,d+1) s.t. ∑ q ∈ N p ω 0 ( p , q ) + ω 1 ( p , q ) + ω 2 ( p , q ) = 1 \text { s.t. } \sum_{\mathbf{q} \in N_{\mathbf{p}}} \omega_{0}(\mathbf{p}, \mathbf{q})+\omega_{1}(\mathbf{p}, \mathbf{q})+\omega_{2}(\mathbf{p}, \mathbf{q})=1 s.t. q∈Np∑ω0(p,q)+ω1(p,q)+ω2(p,q)=1其中 ∑ q ∈ N p ω 0 ( p , q ) + ω 1 ( p , q ) + ω 2 ( p , q ) = 1 \sum_{\mathbf{q} \in N_{\mathbf{p}}} \omega_{0}(\mathbf{p}, \mathbf{q})+\omega_{1}(\mathbf{p}, \mathbf{q})+\omega_{2}(\mathbf{p}, \mathbf{q})=1 ∑q∈Npω0(p,q)+ω1(p,q)+ω2(p,q)=1同样是对参数进行了归一化,保证了 C ( p , d ) C(\mathbf{p}, d) C(p,d)的元素大小, ω \omega ω是一个 K × K K \times K K×K大小可学习卷积核,从上式可以看出,该卷积核一共有三个,分别对应视差 d , d − 1 , d + 1 d, d-1, d+1 d,d−1,d+1,也就是在当前像素的视察的上下层也进行代价聚合,最后加权求和得到最后的视察值,因此对于LGA而言,其输出的权重矩阵大小为 H × W × 3 K 2 × F ( K = 5 ) H \times W \times 3 K^{2} \times F(K=5) H×W×3K2×F(K=5)。
在立体匹配论文笔记(五):GA-Net博客的评论中,有位同学问为什么网络必须加上一个子网络来出SGA和LGA的权重,而不能通过主网络自己学习,作者解释到:
“ 因为卷积核相当于是空间各个位置相同的,但是这里面的SGA和LGA的核应该是空间位置不共享的,应该是和RGB有关的,所以就通过输入一个RGB输出一个各个位置的核”
以上核不共享的观点之后看下源码再确认下,目前我的表面理解是,学习视差其实是一个较难的学习任务,尽管我们通过Cost Volume尽可能减少了难度,但是仍然需要堆积大量的3D卷积来学习中间的关系,GA-Net做的则是通过加入SGA和LGA这样的模块来引入一些先验的规则,进一步降低学习难度,而规则中间涉及的一些参数则通过子网络进行学习。对于该问题的理解,欢迎读者进一步补充。
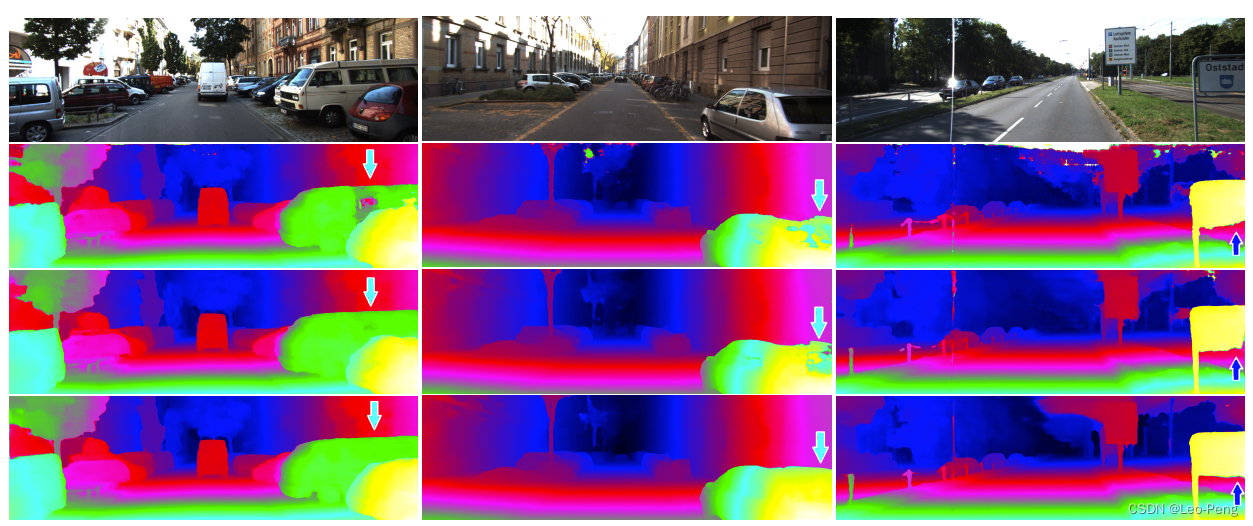
在原论文中,作者对比了通过加入子网络带来的优势,其中第一行为GC-Net的结果,第二行为PSM-Net的结果,第三行为GA-Net的结果