负载调制平衡放大器LMBA理论分析与ADS理想架构仿真
负载调制平衡放大器Load Modulation Balanced PA,简称LMBA是2016年Cripps大佬分析实践的:
An Efficient Broadband Reconfigurable Power Amplifier Using Active Load Modulation
本文ADS工程下载链接:负载调制平衡放大器LMBA理论分析与ADS理想架构仿真-ADS仿真资源
目录
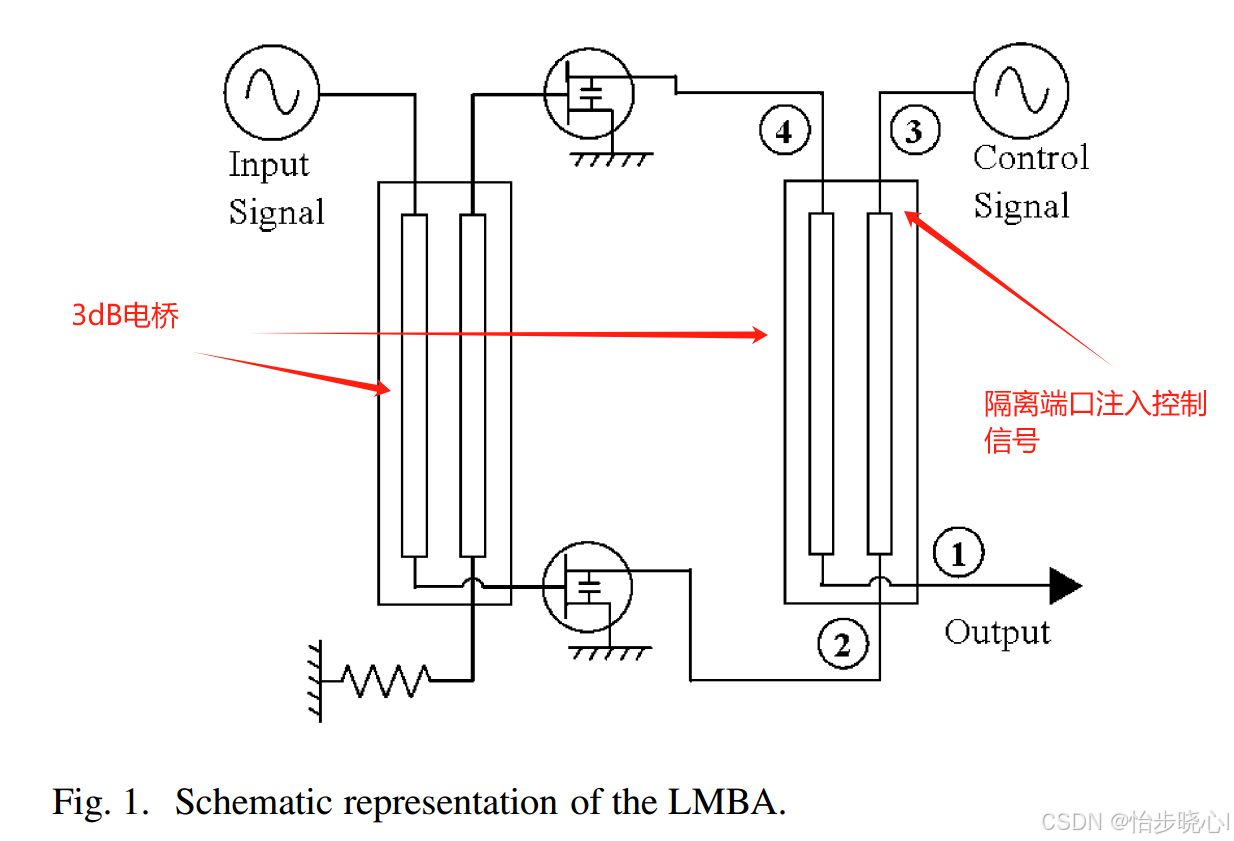
0、LMBA架构简述
0.1、LMBA架构
LMBA本质是是一种双输入的架构,在实现宽带和高回退方面具备优势。但是与常规的双输入的Doherty、Outphasing这种不同,LMBA使用单独的控制信号(CA)对平衡放大器(BA)组进行调制,依据控制信号相位和幅度的不同,可以将平衡功放对的输出阻抗调制到任意位置,即实现完美匹配。
0.2、LMBA架构优势
那么,简单来说,假设我们直接获得了输入信号和控制信号,我们进行LBMA设计时,有如下优势:
1、无需设计输出匹配电路,依靠控制信号将阻抗调为完美匹配点
2、对于宽带情况,使用不同幅度、相位的控制信号就行,宽带能力极强,除了结构中的3dB电桥外无结构限制
但是,宽带电桥是非常常见的,超倍频程也是轻轻松松。
0.3、架构优势原因
实际上,LBMA的特殊性是从隔离端口注入的控制信号,这样平衡功放对可以认为和控制信号隔离,控制信号的输入阻抗恒定50欧姆。对于其他一些DPA或者异相架构,由于使用的是非隔离合路器,多路之间相互调制,复杂度高。
1、LMBA理论推导
1.1 推导理论
LMBA的理论推导非常简单,下面简单说明。
在 LMBA 情况下,两个平衡设备表示为电流吸收器,具有相等的幅度
I
b
{I}_{b}
Ib和适当的90°相位偏移。
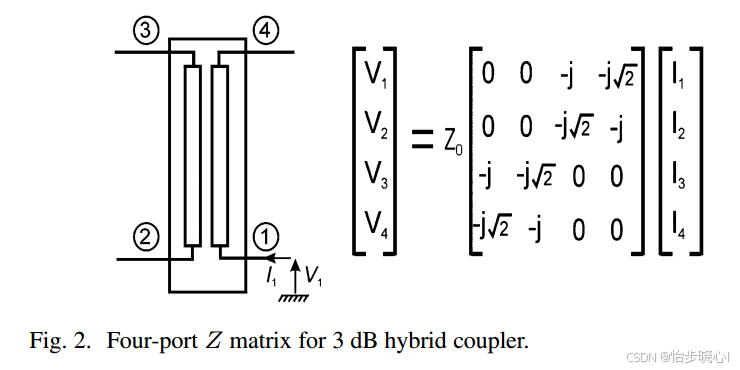
因此,假设如上架构图中3dB电桥2端口电流为 I 2 = − I b I_{2}=-I_{b} I2=−Ib,对应的4端口电流为 I 4 = − j I b I_{4}=-jI_{b} I4=−jIb,两者相位差90°。
控制信号从3端口注入,其电流假设为 I 3 = I c o n = − j I c e j ϕ I_{3}=I_{\mathrm{con}}=-jI_{c}e^{j\phi} I3=Icon=−jIcejϕ。 自然, I c I_{c} Ic是控制信号的幅值, ϕ \phi ϕ是控制信号的相位。
电桥的1端口是输出端口,接的是50欧姆负载,因此有: V 1 = − Z 0 I 1 {V}_{1}=-Z_{0}I_{1} V1=−Z0I1
而对于一个理想的电桥,其4端口的电压、电流关系如下所示:
结合上面的方程,即可求解得到平衡功放对的输出阻抗(ZA和ZB其实就是电桥2、3端口的输出阻抗):
Z
A
=
Z
0
(
1
−
2
I
c
e
j
ϕ
I
b
)
Z
B
=
Z
0
(
1
−
2
I
c
e
j
ϕ
I
b
)
Z_{A}=Z_{0}\left(1-\sqrt2\frac{I_{c}e^{j\phi}}{I_{b}}\right)\\Z_{B}=Z_{0}\left(1-\sqrt2\frac{I_{c}e^{j\phi}}{I_{b}}\right)
ZA=Z0(1−2IbIcejϕ)ZB=Z0(1−2IbIcejϕ)
1.2 Matlab推导代码
使用Matlab进行自动的公式推导,求解得到的Matlab代码如下:
clc
clear
syms Ib Ic phi Z0 I1 ZA ZB
I2=-Ib;
I4=-1j*Ib;
I3=-1j*Ic*exp(1j*phi);
V1=(-1j*I3-1j*sqrt(2)*I4)*Z0;
V2=(-1j*I4-1j*sqrt(2)*I3)*Z0;
V3=(-1j*I1-1j*sqrt(2)*I2)*Z0;
V4=(-1j*I2-1j*sqrt(2)*I1)*Z0;
eqn(1)=V1==-I1*Z0;
eqn(2)=ZA==V2/I2;
eqn(3)=ZB==V4/I4;
sol = solve(eqn, [ZA ZB I1], 'ReturnConditions', true);
pretty(simplify(sol.ZA))
pretty(simplify(sol.ZB))
从最终的结果来看,似乎和原作者差了一个负号,可以是哪边参考方向搞错了,在此不深究了。
2、ADS对理想LMBA仿真
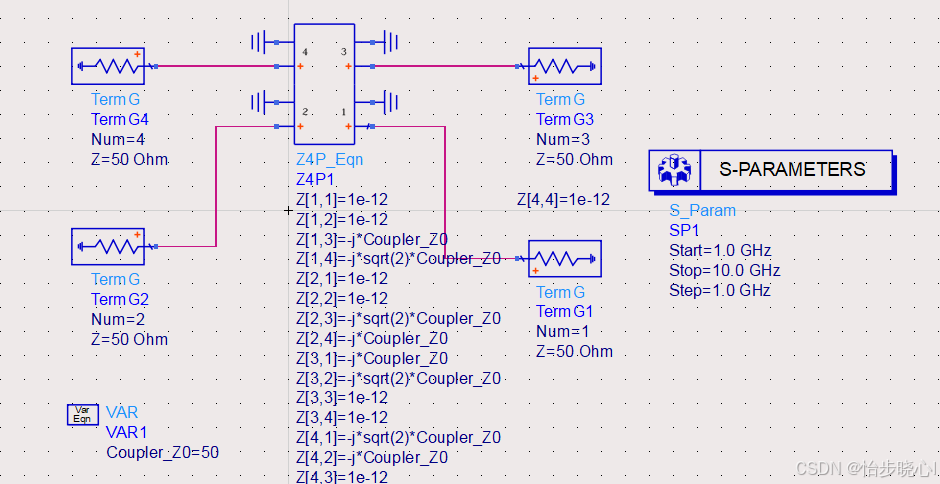
2.1 ADS理想3dB电桥构建
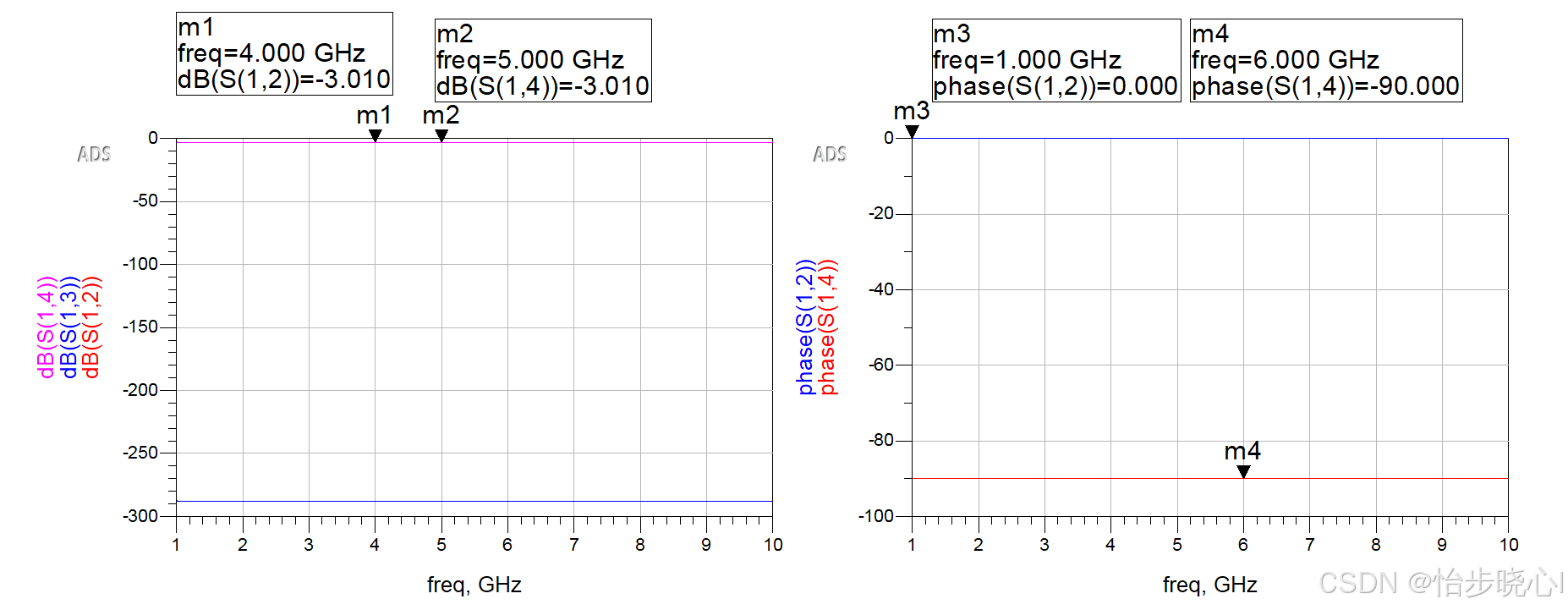
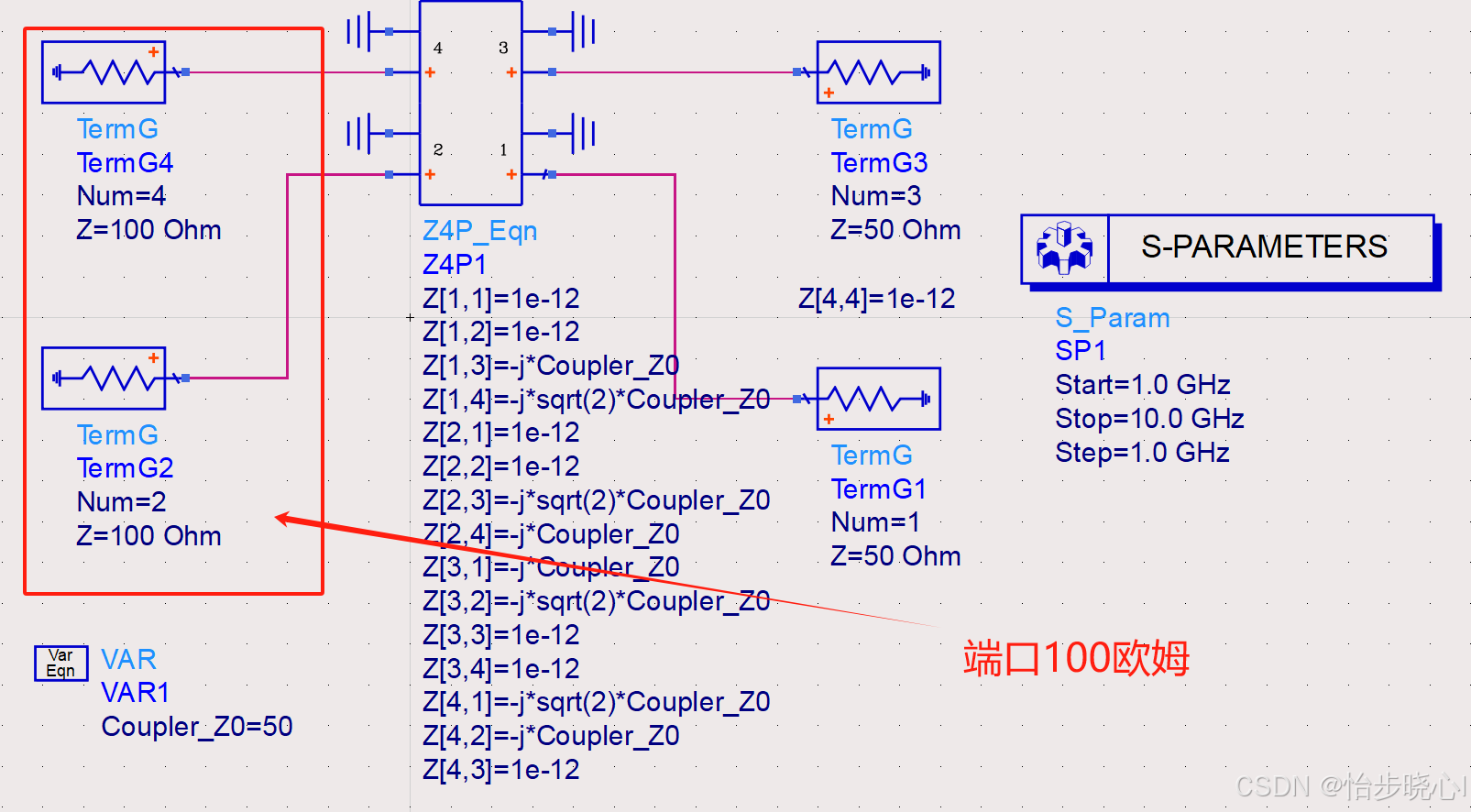
把论文中给出的Z参数矩阵带入到ADS的控件之中,模拟理想3dB电桥器件。这部分具体操作可以参考:在ADS中使用传输端口参数构建理想元器件模型—以3dB电桥为例。最终的结果如下所示:
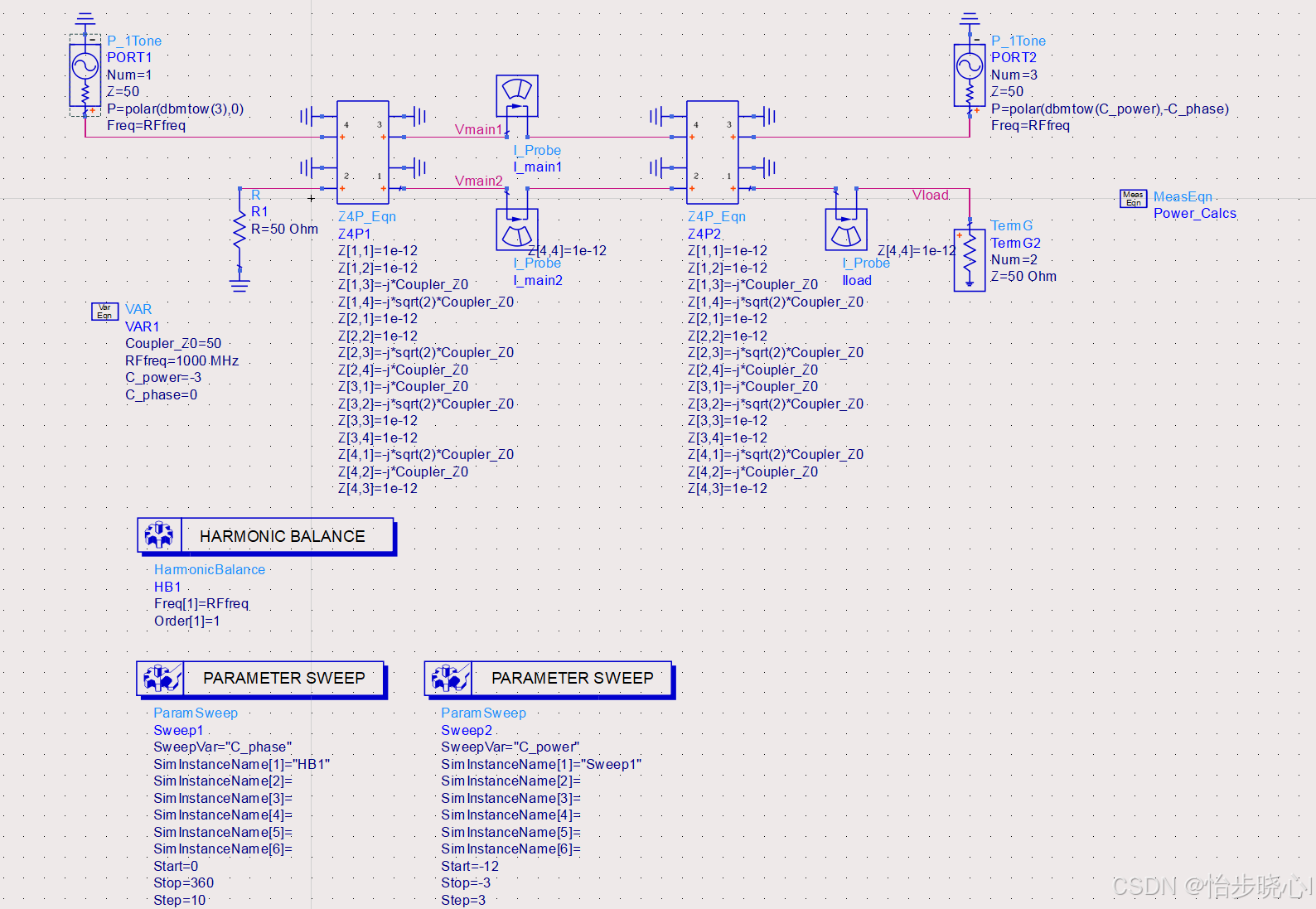
2.2 ADS理想LMBA架构搭建
按照大佬论文中的框架图,可以搭建为如下的LMBA理想架构。可以看到,需要对控制信号的幅度和相位进行扫描:
2.3 ADS理想LMBA仿真结果分析
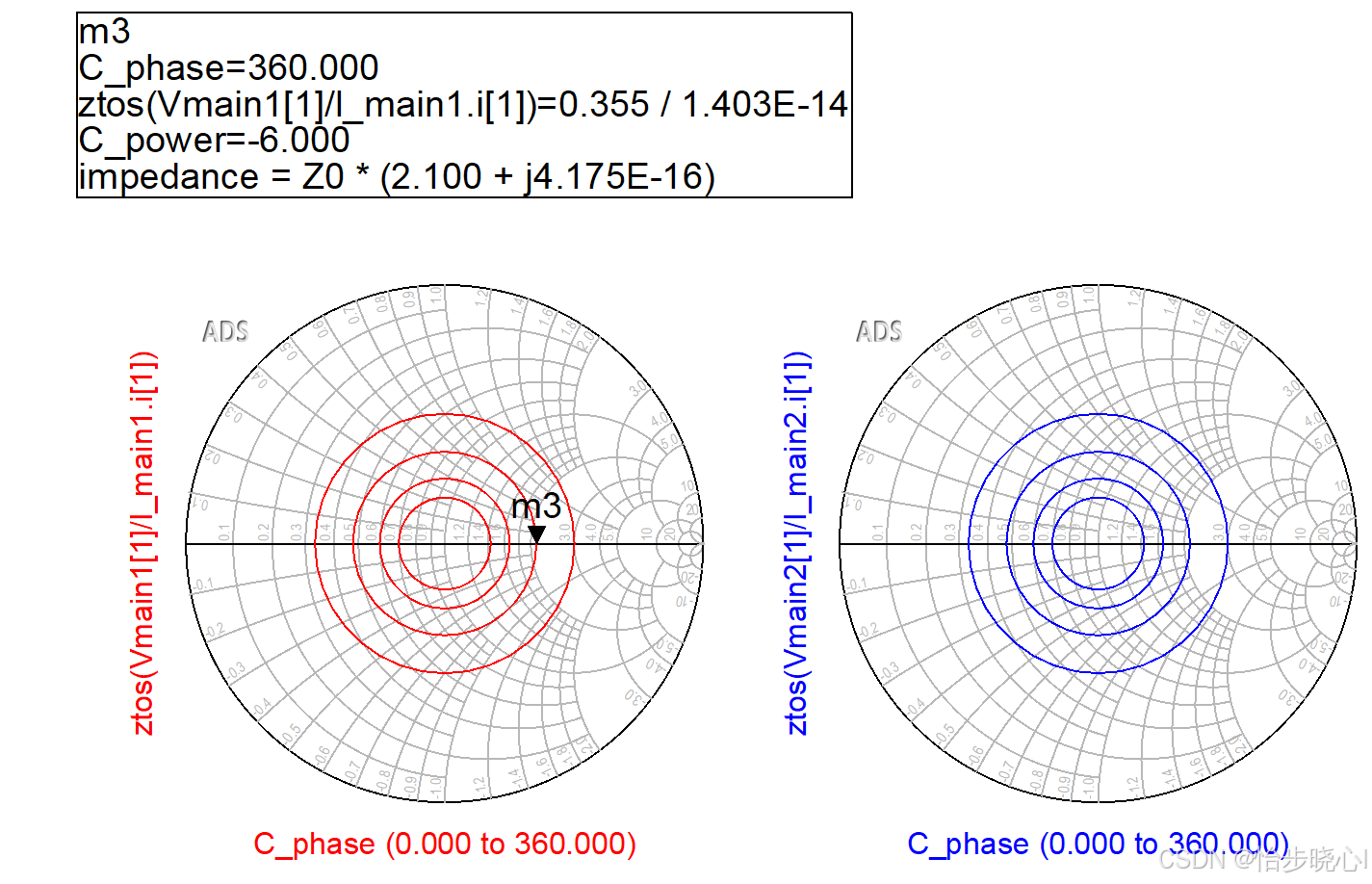
2.3.1 阻抗调制分析
通过仿真可以看到在控制信号幅度、相位改变时两个平衡功放的阻抗曲线。可以看到在控制PA输出功率比平衡对单个PA输出功率小6dB时,即可将输出阻抗调制到100欧姆,可以理解为从Ropt调制到2Ropt,这也是经典Doherty在回退时的调制能力。
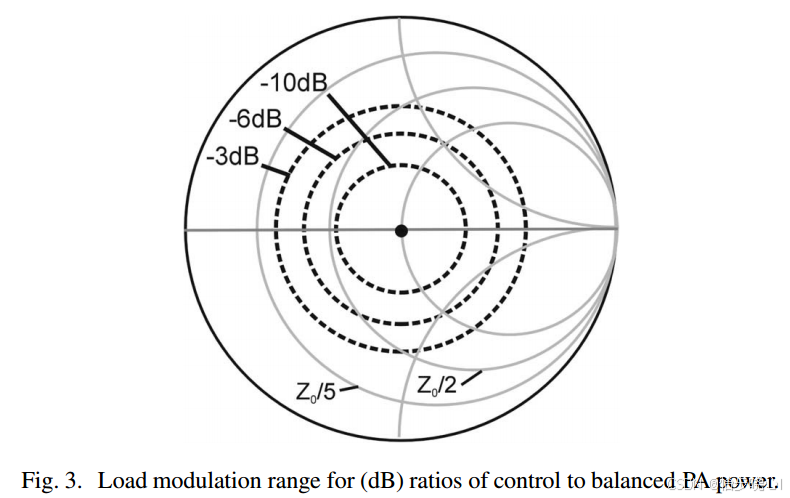
可以看到得到的仿真结果和Cripps论文中的一致,下面这是论文原图:
2.3.2 输出效率分析
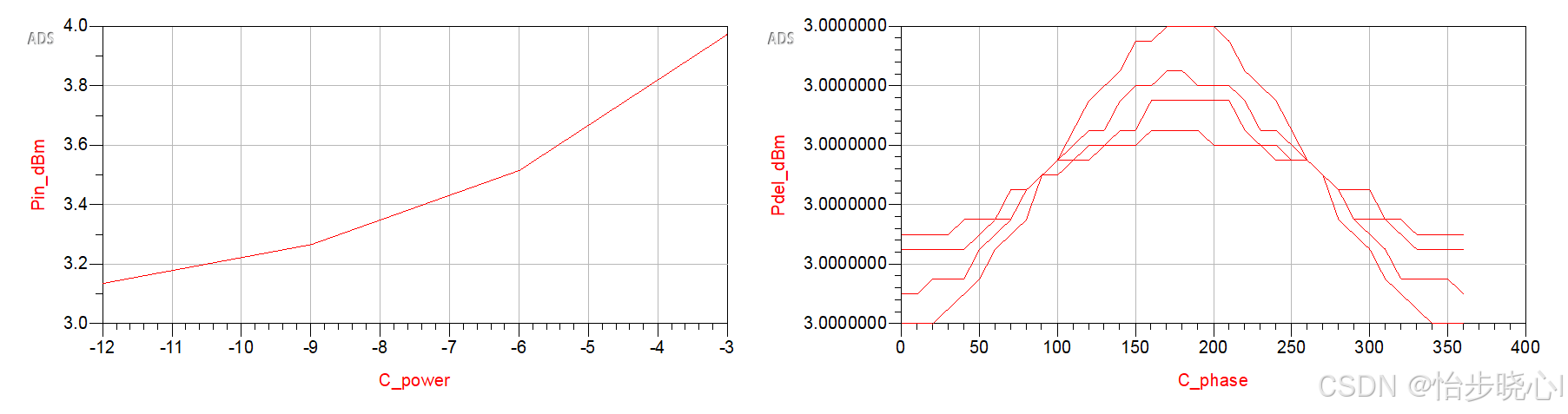
Cripps原文中这样描述:可以通过调整控制信号的幅度和相位来“调制”每个平衡设备输出端的负载,并且对于每个平衡端口,产生的阻抗具有相同的幅度和相位。此外,辅助放大器产生的功率作为端口 1 输出的一部分完全恢复。
也就是说,控制信号的输入功率会到最终的输出端口,但是实际的仿真结果却有出入。从下图可以看到,无论输入的总功率是多少,输出都是恒定在3dBm:
经过分析,这是由于失配导致的,将在下面进行分析。但是对于原文所描述的辅助放大器产生的功率作为端口 1 输出的一部分完全恢复,依旧是无法理解,懂行的可以指导一下。
2.3.3 输出效率分析结果验证-3dB耦合器失配仿真
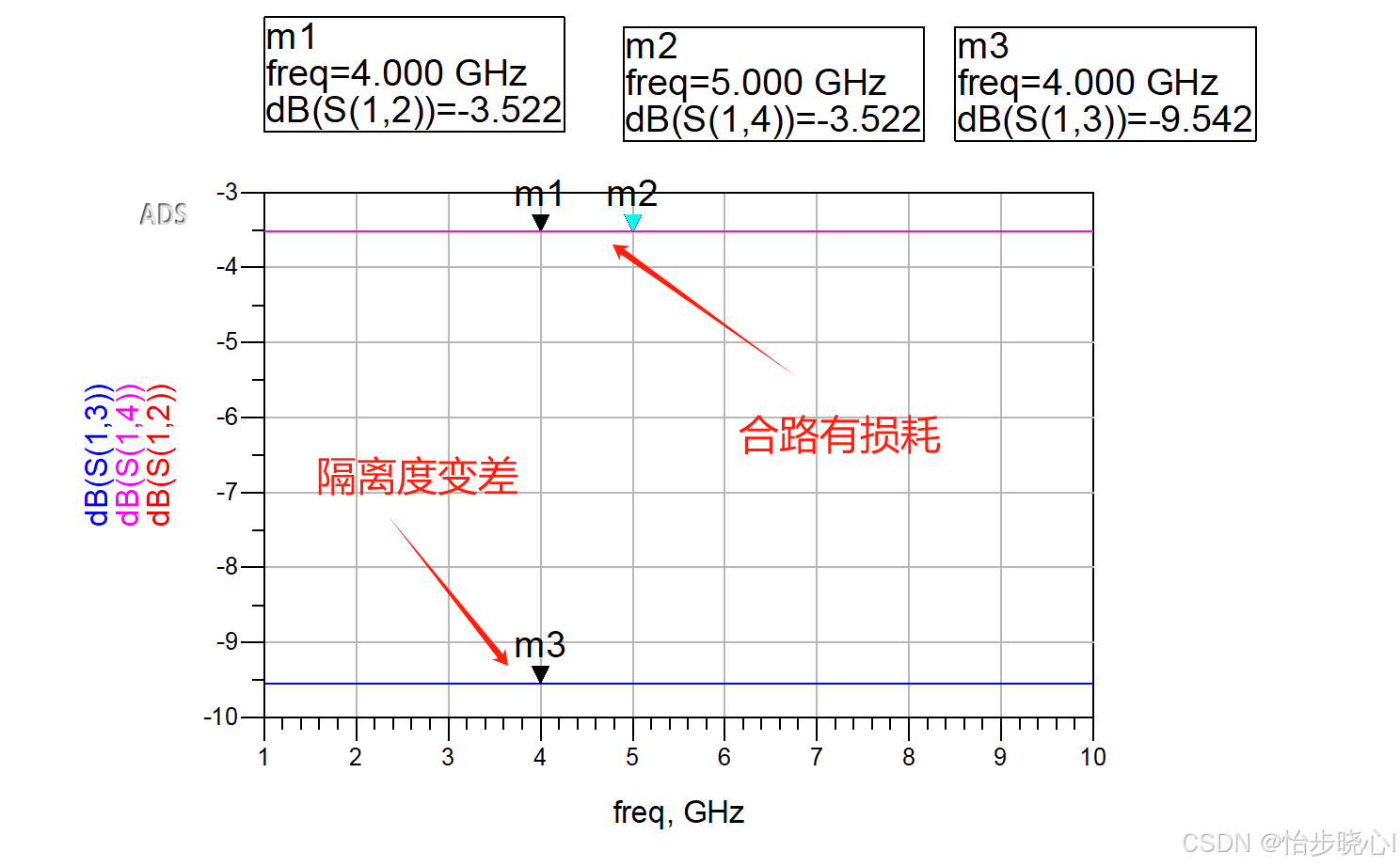
假设在控制放大器输出-6dBm信号的情况下,此时平衡功放对的阻抗都被调制到100欧姆,也就是2Ropt的6dB回退状态。此时对合路所使用的耦合器进行分析:
显而易见,实际上此时的3dB合路电桥工作在失配的状态,此时会存在无可避免的合路损耗,可以看到每路合路是-3.5dB左右,正常来说-3dB才是完美合路。在失配状态,虽然合路效率变差,但是控制信号到输出端口的隔离度也变差了,部分控制信号成为了输出端口的输出,因此合路依旧维持了3dBm的输出:
总之,从分析和仿真来看,控制信号好像不会全部注入到输出中去。对平衡功放的阻抗调制会导致3dB电桥端口的失配,导致合路效率降低,但是此时失配也会有部分控制信号注入到合路,导致最终合路的输出功率恒定。
分析有问题敬请指出,因为部分分析结果和原文有出入。