0. 写在前面

这学期的多元统计分析课程安排了个presentation，主题任意，我就想到了一个我感兴趣的东西——kmeans算法的一大问题在于最优k值不好确定，那我能不能改进一下这个算法，使它能够自动寻找最优的k值并聚类呢？

说干就干，我也确实做出了一些结果，但感觉做得一般，就不水论文了，干脆开源发出来。

1. Kmeans聚类算法

与分类算法不用，聚类算法在未知样本标签的前提下，通过数据之间的内在关系将样本划分为若干类别，使同一类别之间的样本尽可能相似，不同类别之间的样本尽可能不同。

K均值（kmeans）算法是一个应用广泛的聚类算法，属于无监督学习算法的一种。其主要思想为随机选取k个样本点作为初始聚类（簇）中心点；对剩余的每个样本，根据其与各簇中心的相似度（距离），将它划分给与其最相似的簇中心所对应的簇；然后重新计算每个簇中心所有样本的平均值作为新的簇中心。

不断重复以上过程，直到代价函数收敛，即簇中心不再发生明显的变化。通常采用均方误差，也就是各个样本距离所属簇中心点的误差平方和（SSE）作为代价函数。

$$J(c,\mu )=\sum _{i=1}^N||x_i-{\mu }_{c_i}|{|}^2$$

其中，$x_i$表示第i个样本，$c_i$是$x_i$所属的簇，${\mu }_{c_i}$代表簇对应的中心点，$N$为样本总数。

算法流程如下：

1. 数据预处理，包括标准化，异常值处理等；
2. 随机选取k个样本作为初始簇中心，记为${\mu }_1^{(0)},{\mu }_2^{(0)},\cdots ,{\mu }_k^{(0)}$；
3. 计算代价函数：$J(c,\mu )=\underset{\mu }{\min }\underset{c}{\min }\sum _{i=1}^N||x_i-{\mu }_{c_i}|{|}^2$；
4. 令$t=0,1,2,\dots$为迭代步数，重复以下过程直至代价函数收敛。
   • 对于每一个样本$x_i$，将其划分到距离最近的簇：$c_i^{(t)}\leftarrow \underset{k}{\mathrm{argmin}}||x_i-{\mu }_k^{(t)}|{|}^2$；
   • 对于每一个类簇$k$，重新计算该类簇的中心:${\mu }_k^{t+1}\leftarrow \underset{\mu }{\mathrm{argmin}}\sum _{i:c_i^{(t)}=k}||x_i-\mu |{|}^2$。

相比于其他聚类算法，kmeans聚类算法计算速度快，高效，可伸缩，可应用于大规模数据集。但也存在以下一些缺点：

• k值需要预先人为给定；
• 不同的初始聚类中心会得到不同的聚类结果；
• 由于采用欧氏距离作为距离度量，容易受离群点影响，因此必须先对数据做归一化。

2. 聚类评估指标

聚类评估指标分为两种，一种是内部评估指标，评价聚类结果的凝聚性和分离性；另一种是外部评估指标，如兰德系数等，由于引入了样本的真实标签，所以此时的聚类实际上是分类问题，为有监督学习。本文主要讨论在没有真实标签情况下的聚类问题。

2.1 内部评价指标

• 轮廓系数（Silhouette Coefficient）：
  $$s=\frac{b-a}{max(a,b)}$$
  其中$a$为簇内凝聚度，定义为样本点与同类其他点之间的平均距离；$b$为簇间分离度，定义为样本与相邻簇中所有样本点之间的平均距离。由计算公式可以看到，轮廓系数的取值范围在$[-1,1]$，且轮廓系数越接近于1，说明两个簇之间分离得越远，簇内分布越密集，聚类效果越好。
  

• CH指标（Calinski-Harabasz index）：
  定义类内离差矩阵为$$W_k=\sum _{q=1}^k\sum _{x\in C_q}(x-c_q)(x-c_q{)}^T$$ 类间离差矩阵为 $$B_k=\sum _{q=1}^k{n}_q(c_q-c_E)(c_q-c_E{)}^T$$ 其中$C_q$表示簇$q$的点集，$c_q$表示簇$q$的中心点，$c_E$表示簇$E$的中心点，$n_q$表示簇$q$的点的个数。则CH指数的计算公式为：$$\begin{array}{r}CH=\frac{tr(B_k)}{tr(W_k)}\times \frac{n_E-k}{k-1}\end{array}$$其中$tr(B_k)$和$tr(W_k)$分别为类间离差矩阵$B_k$和类内离差矩阵$W_k$的迹（trace）。CH指标由分离度与紧密度的比值得到，且CH指标越大，说明类自身越紧密，类与类之间越分散，聚类结果越好。
  

• 戴维森堡丁指标（Davies-Bouldin Index）：
  DB指标用类内样本点到其聚类中心的距离估计类内的紧密度，用聚类中心之间的距离表示类间的分离度。其计算公式为：
  $$DB=\frac{1}{k}\sum _{i=1}^k\underset{j\ne i}{\max }\frac{\overline{C_i}+\overline{C_j}}{||w_i-w_j|{|}_2}$$
  DB指标越小，说明类自身的点分布越紧密，类与类之间越分散，聚类效果越好。
  

2.2 外部评价指标

• 兰德系数（Rand Index）
  给定真实标签$C$，聚类标签$K$，定义$a$为在 $C$中的相同集合与$K$中的相同集合中的元素对数，换句话说，$a$表示两个点在$C$中属于统一类别，且在$K$中属于同一簇；定义$b$为在$C$中的不同集合与$K$中的不同集合中的元素对数，即两个点不属于$C$中同一类别，且在$K$中不属于同一簇。
  兰德系数计算公式如下：
  $$RI=\frac{a+b}{C_2^{n_{sample}}}$$
  其中$C_2^{n_{sample}}$表示数据中的所有可能组合的对数。
  兰德系数类似于准确率，取值范围在$[0,1]$，取值越接近于1说明聚类划分越准确，效果越好。
  

  但是, 兰德系数并不能保证随机标签分配会得到接近于0的值。为去除随机标签对于兰德系数的影响，一般常用调整兰德系数来衡量聚类效果，其定义如下：
  $$ARI=\frac{RI-E[RI]}{max(RI)-E[RI]}.$$

• V-measure
  V-measure类似于分类评估指标中的F-score，是融合同质性和完整性的综合评价指标。
  同质性（homogeneity）：每个簇只包含一个类的成员。
  完整性（completeness）：给定类的所有成员都分配给同一个簇。
  同质性和完整性的具体计算公式参见参考资料[1]。V-measure的计算公式如下：
  $$v=\frac{(1+\beta )\times homogeneity\times completeness}{(\beta \times homogeneity+completeness)}$$
  其中$\beta$为权重参数，$\beta$越大，同质性的比重则越大。V-measure得分越接近于1，同质性和完整性越强，聚类划分越趋近于理想状态，效果越好。
  
  

• 互信息（mutual information）：
  互信息是度量两个标签分配一致性的函数，忽略排列，且有两个不同的归一化版本，Normalized Mutual Information (NMI) 和 Adjusted Mutual Information (AMI)。具体的计算公式参见参考资料[1]。调整互信息（AMI）有两个好处，一是对于随机的标签分配，AMI评分接近于0；二是它是有界的，AMI趋于0说明标签分配之间是独立的，即聚类结果和真实结果完全不匹配；AMI恰好为1时，说明两个标签是完全相等的（无论是否排列过），即聚类结果和真实结果完全匹配。
  
  

3. 寻找最优k值的方法

k值的选择一直是kmeans算法的一大难题。k值越大，聚类数量越多，每个类会越紧密，但也伴随着更高的计算量，且聚类数量过多有时候反而不利于实际应用。常见的寻找最优k值的方法主要有手肘法、最大化轮廓系数法和Gap Statistic等。限于篇幅，这里只介绍前两种方法：

3.1 手肘法

手肘法是基于多次实验的结果。随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。并且，当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。

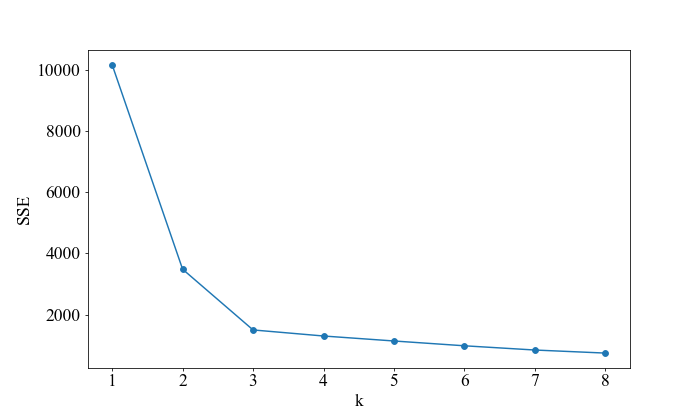
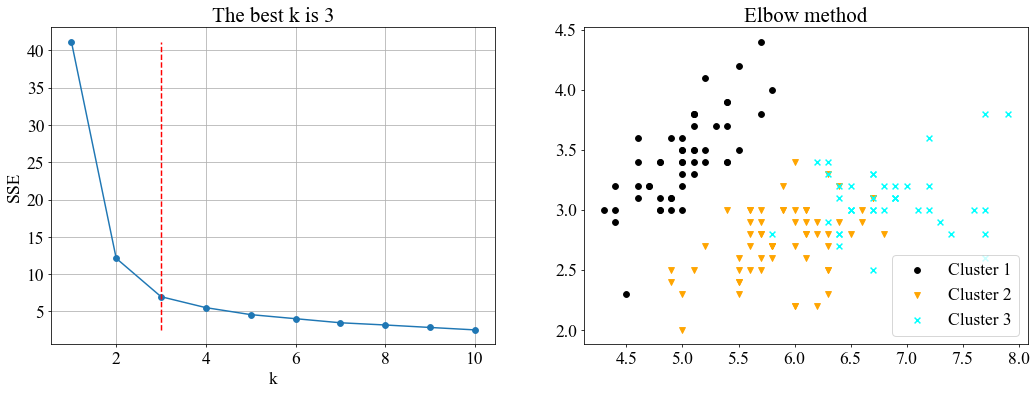
尝试不同的k值，并将不同k值对应的损失函数（SSE）画成折线，横轴为k值，纵轴为误差平方和（SSE）定义的损失函数。

由图可见，k值越大，距离平方和越小，聚类越紧密；当$k\le 3$时，误差平方和迅速减小；当$k>3$时，误差平方和曲线变得平缓，衰减缓慢。此时手肘法认为$k=3$是最优k值。

手肘法虽然简单直接，但不够自动化，选取最优k值需要人用肉眼去观察，不同人得出的最优k值可能不同，存在一定的主观性。

3.2 最大化轮廓系数法

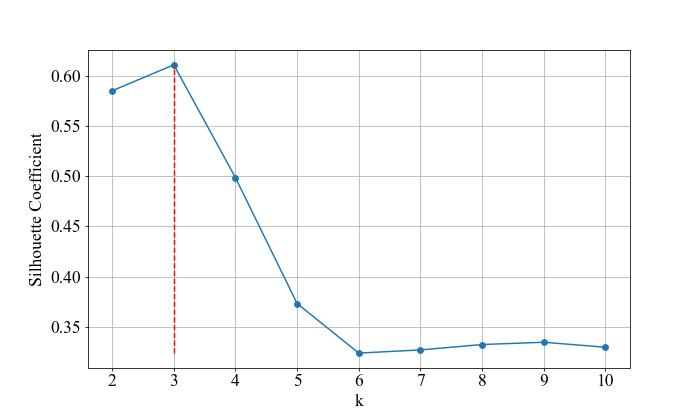
顾名思义，选取使轮廓系数最大的k值作为最优k值。轮廓系数越接近于1，说明类自身分布越紧密，类与类之间相隔越远，聚类效果越好。

上图可以看出，轮廓系数最大的值对应的k值为3，故最优k值为3。

4. 算法改进尝试

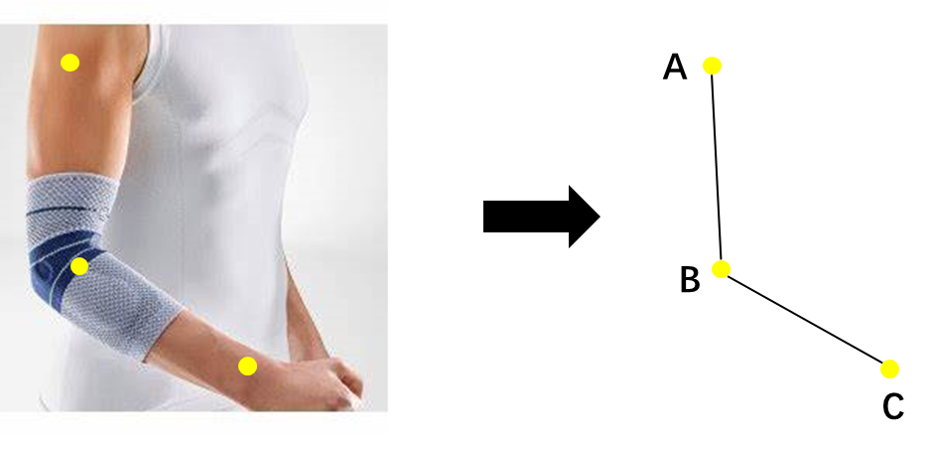
手肘法是一个较为不错的选取最优k值的经验方法，但不够自动化，为此，本文重点将手肘法选k值的过程自动化。手肘法关键在于找到位于手肘位置的点，简称手肘点。手肘点有何特征呢？先来上一张图：

从大臂、小臂、手肘部位各选取一个点，然后连接成线，如上图右侧所示。可以看到，手肘点为点B，且手肘点前后线段斜率相差较大，线段AB较为陡峭，其斜率绝对值较大；线段BC较为平缓，其斜率绝对值较小。由此，我们可以定义手肘点为前后线段斜率相差较大的点。进一步，斜率在数学上是什么？一阶导数。某点前后线段斜率的比值是什么？二阶导数。因此，直观上看，手肘点也就是二阶导数最大的点。

按照这个思想，我设计出了改进手肘法的第一个版本：

Version 1

设k的取值集合为 K = { k 1 , k 2 , ⋯   , k n } K = \{k_1, k_2, \cdots, k_n\} K={k1​,k2​,⋯,kn​}，记
$$SSE(k_j)=\sum _{i=1}^N||x_i-{\mu }_{c_i}|{|}^2,j=1,2,\dots ,n\text{\hspace{1em}(1)}$$
为$k_j$对应的损失函数值，即误差平方和。定义一阶导数为
$$SS{E}^{\prime }(k_j)=\{\begin{array}{ll}\frac{SSE(k_{j+1})-SSE(k_j)}{2}& j=1,2,\dots ,n-1\\ 0& j=n\end{array}\text{\hspace{1em}(2)}$$
集合$K$的首尾端点$k_1,k_n$的两端均只有一条线段，如上图中的点A，C，分别只能求出一条线段的斜率，故这里我们将首尾端点的二阶导数的值定义为0。具体定义如下：
$$SS{E}^{\prime \prime }(k_j)=\{\begin{array}{ll}\frac{SS{E}^{\prime }(k_j)-SS{E}^{\prime }(k_{j-1})}{2}& j=2,3,\dots ,n-1\\ 0& j=1,n\end{array}\text{\hspace{1em}(3)}$$

算法步骤如下：

1. 对数据进行min-max标准化；
2. k从设定的最小k值 $mi{n}_k$ 到最大k值 $ma{x}_k$ 轮流取值，训练k-means模型，并记录误差平方和 S S E = { S S E ( k 1 ) , S S E ( k 2 ) , … , S S E ( k n ) } SSE = \{SSE(k_1),SSE(k_2), \dots, SSE(k_n) \} SSE={SSE(k1​),SSE(k2​),…,SSE(kn​)}；
3. 用公式（2）计算SSE的一阶导数： S S E ′ = { S S E ′ ( k 1 ) , S S E ′ ( k 2 ) , … , S S E ′ ( k n ) } SSE' = \{SSE'(k_1),SSE'(k_2), \dots, SSE'(k_{n}) \} SSE′={SSE′(k1​),SSE′(k2​),…,SSE′(kn​)}；
4. 用公式（3）计算SSE的二阶导数： S S E ′ ′ = { S S E ′ ′ ( k 1 ) , S S E ′ ( k 2 ) , … , S S E ′ ( k n ) } SSE'' = \{SSE''(k_1),SSE'(k_2), \dots, SSE'(k_{n}) \} SSE′′={SSE′′(k1​),SSE′(k2​),…,SSE′(kn​)}；
5. 选取最优k值：$k^{\ast }=argmax(SS{E}^{\prime \prime })$。

算法代码如下：

def Elbow_v1(X, max_k=10, min_k=2):
    '''
    改进手肘法版本1：用SSE的二阶导数绝对值最大值所在的k值作为最优k值。

    parameter:
    X: input data, ndarray.
    max_k: the maximum value of k, should be smaller than the number of samples, positive integer.
    min_k: the minimum value of k, should be at least 1, postive integer.

    '''
    
    assert min_k >= 1
    assert max_k < X.shape[0]-1

    Scaler = StandardScaler()
    X = Scaler.fit_transform(X)
    # X = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
    k_list = list(range(min_k, max_k+1))

    SSE = [] 
    estimator_history = []
    for k in k_list:
        estimator = KMeans(n_clusters=k)  
        estimator.fit(X)  
        estimator_history.append(estimator)
        SSE.append(estimator.inertia_)

    SSE = np.array(SSE)
    
    SSE_delta = [] #一阶导数的绝对值
    for i in range(len(SSE)-1):
        SSE_delta.append((SSE[i+1] - SSE[i]) / 2)

    SSE_delta2 = [0]  #二阶导数的绝对值
    for i in range(len(SSE_delta)-1):
        SSE_delta2.append((SSE_delta[i+1] - SSE_delta[i]) / 2)

    SSE_delta.append(0)
    SSE_delta2 += [0]
    for i in range(len(k_list)):
        print('k = %d, SSE = %.4f, SSE_delta = %.4f, SSE_delta2 = %.4f'%(k_list[i], SSE[i], SSE_delta[i], SSE_delta2[i]))

    SSE_delta2 = np.array(SSE_delta2)
    ind_max = np.argmax(SSE_delta2)
    best_k = k_list[ind_max]
    best_estimator = estimator_history[ind_max]
    print('Best k = ', best_k)

    return best_estimator, best_k, SSE

接下来我们做实验来验证算法的可靠性。首先生成含有3个类别的模拟数据：

from sklearn.datasets import make_blobs
centers = [[1, 2], [-1, -1], [1, -1]]
n_clusters = len(centers)
X2, labels_true = make_blobs(n_samples=3000, centers=centers, cluster_std=0.5)

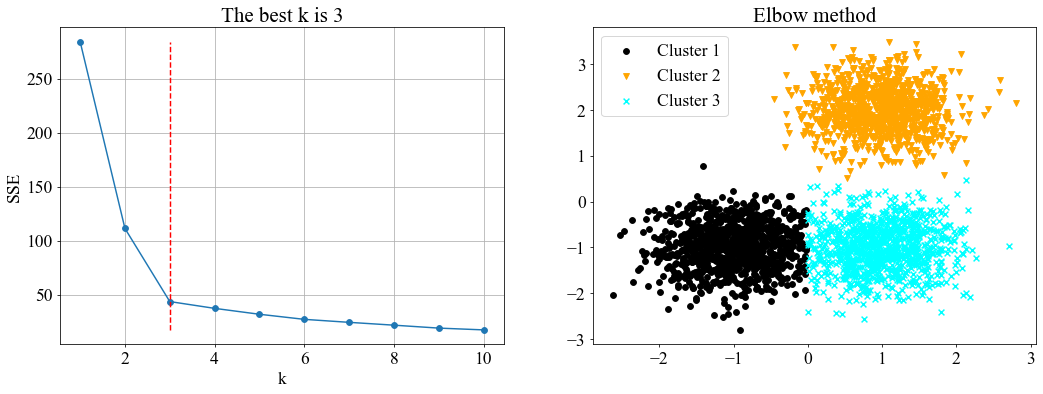
算法结果如下：

可以看到这个结果并不好。从左侧图可以看出最优k值应该为3，但算法却将最优k值给到了2；右图也可以看出数据的实际分布应该有3个类别。从算法流程结果可以看到，当$k=1,2$时，对应的一阶导数$SS{E}^{\prime }$的绝对值都比较大，两者相减后的绝对值仍然较大，导致得到的二阶导数数值较大，促使算法把最优k值赋给了2。

进一步分析，上文定义的二阶导数是绝对指标，不是相对指标，难以刻画某点前后线段斜率的变化。为此，我重新定义了各阶变化率，采用相对指标来描述某点前后线段斜率的变化大小，设计出了改进手肘法的第二个版本：

Version 2

设k的取值集合为 K = { k 1 , k 2 , ⋯   , k n } K = \{k_1, k_2, \cdots, k_n\} K={k1​,k2​,⋯,kn​}，仍然记
$$SSE(k_j)=\sum _{i=1}^N||x_i-{\mu }_{c_i}|{|}^2,j=1,2,\dots ,n$$
为$k_j$对应的损失函数值，即误差平方和。定义SSE的一阶相对变化率为
$$SS{E}^{\prime }(k_j)=\{\begin{array}{ll}\frac{|SSE(k_{j+1})-SSE(k_j)|}{SSE(k_j)}& j=1,2,\dots ,n-1\\ 0& j=n\end{array}\text{\hspace{1em}(4)}$$
注意这里采用了相对指标，且对分子取了绝对值，由此可以看出k值每增加1时SSE的变化百分比。
类似地，定义SSE的二阶相对变化率如下：
$$SS{E}^{\prime \prime }(k_j)=\{\begin{array}{ll}\frac{|SS{E}^{\prime }(k_j)-SS{E}^{\prime }(k_{j-1})|}{SS{E}^{\prime }(k_{j-1})}& j=2,3,\dots ,n-1\\ 0& j=1,n\end{array}\text{\hspace{1em}(5)}$$
SSE随着k的增大而单调递减。当k小于最优k值时，SSE会迅速下降，此时斜率的绝对值较大；当k大于最优k值时，SSE衰减缓慢，趋于平缓，此时斜率的绝对值较小；当k为最优k值时，前后两段线段的斜率相差较大，即该点的二阶相对变化率最大，这就是改进手肘法版本2的核心思想。

算法步骤如下：

1. 对数据进行min-max标准化；
2. k从设定的最小k值 $mi{n}_k$ 到最大k值 $ma{x}_k$ 轮流取值，训练k-means模型，并记录误差平方和 S S E = { S S E ( k 1 ) , S S E ( k 2 ) , … , S S E ( k n ) } SSE = \{SSE(k_1),SSE(k_2), \dots, SSE(k_n) \} SSE={SSE(k1​),SSE(k2​),…,SSE(kn​)}；
3. 用公式（4）计算SSE的一阶变化率： S S E ′ = { S S E ′ ( k 1 ) , S S E ′ ( k 2 ) , … , S S E ′ ( k n ) } SSE' = \{SSE'(k_1),SSE'(k_2), \dots, SSE'(k_{n}) \} SSE′={SSE′(k1​),SSE′(k2​),…,SSE′(kn​)}；
4. 用公式（5）计算SSE的二阶变化率： S S E ′ ′ = { S S E ′ ′ ( k 1 ) , S S E ′ ′ ( k 2 ) , … , S S E ′ ′ ( k n ) } SSE'' = \{SSE''(k_1),SSE''(k_2), \dots, SSE''(k_{n}) \} SSE′′={SSE′′(k1​),SSE′′(k2​),…,SSE′′(kn​)}；
5. 选取最优k值：$k^{\ast }=argmax(SS{E}^{\prime \prime })$。

代码如下：

def Elbow(X, max_k=10, min_k=2):
    '''
    手肘法版本2，用二阶相对变化率最大的点作为作为最优k值。

    parameters:
    input:
    X: input data, ndarray.
    max_k: the maximum value of k, should be smaller than the number of samples, positive integer.
    min_k: the minimum value of k, should be at least 1, postive integer.

    output:
    best_estimator: the best kmeans estimator corresponding to the optimal k.
    best_k: the optimal value of k.
    SSE: the history of SSE corresponding to the k_list: [min_k, min_k+1, ..., max_k].
    '''
    
    assert min_k >= 1
    assert max_k < X.shape[0]-1

    Scaler = StandardScaler()
    X = Scaler.fit_transform(X)
    # X = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
    k_list = list(range(min_k, max_k+1))

    SSE = [] 
    estimator_history = []
    for k in k_list:
        estimator = KMeans(n_clusters=k)  
        estimator.fit(X)  
        estimator_history.append(estimator)
        SSE.append(estimator.inertia_)

    SSE = np.array(SSE)
    
    SSE_delta = [] #一阶相对变化率
    for i in range(len(SSE)-1):
        SSE_delta.append(abs(SSE[i+1] - SSE[i]) / SSE[i])

    SSE_delta2 = [0]  #二阶相对变化率
    for i in range(len(SSE_delta)-1):
        SSE_delta2.append(abs(SSE_delta[i+1] - SSE_delta[i]) / SSE_delta[i])

    SSE_delta.append(0)
    SSE_delta2 += [0]
    for i in range(len(k_list)):
        print('k = %d, SSE = %.4f, SSE_delta = %.4f, SSE_delta2 = %.4f'%(k_list[i], SSE[i], SSE_delta[i], SSE_delta2[i]))

    SSE_delta2 = np.array(SSE_delta2)
    ind_max = np.argmax(SSE_delta2)
    best_k = k_list[ind_max]
    best_estimator = estimator_history[ind_max]
    print('The best k is: ', best_k)

    return best_estimator, best_k, SSE

5. 实验

接下来做几个实验来验证版本2算法的可靠性。

• 实验一：继续采用版本1的数据，结果如下：

其中，MAX SH-score表示最大化轮廓系数法。注意这个时间是最佳k值对应的kmeans模型的拟合时间，不是本文提出的算法的耗时。

从上表的结果可以看到，最大化轮廓系数法和手肘法版本2都找到了最优k值，评价指标的结果基本相同。

• 实验二：鸢尾花数据集。

from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target

算法结果：

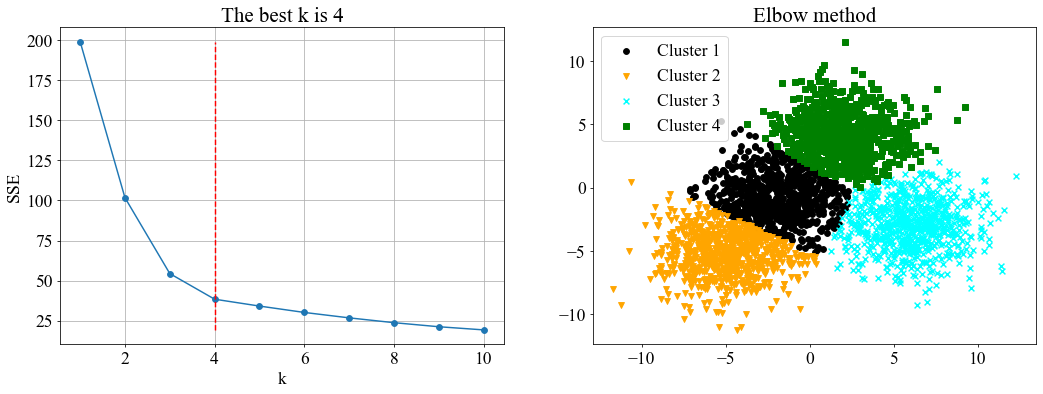
• 实验3：生成一个含有4个类别的数据集：

centers2 = [[-5, -5], [-2, -1], [6, -3], [2, 4]]
X3, labels_true = make_blobs(n_samples=3000, centers=centers2, cluster_std=2)

算法结果：

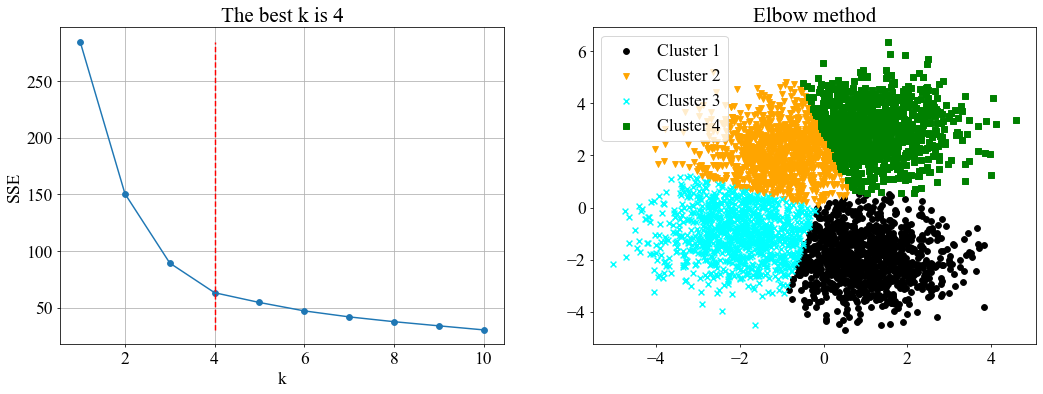
• 实验4：生成一个含有4个类别的数据集（但数据分布更紧密，难度加大）：

centers3 = [[-1, 2], [-2, -1], [1, 3], [1, -2]]
X4, y4 = make_blobs(n_samples=4000, centers=centers3, cluster_std=1)

以上4个实验中，不同方法得到的k值不尽相同。

从聚类的内部评估指标（SSE和轮廓系数）结果来看，改进手肘法版本2的SSE在四个数据集上都达到了最小，说明聚类结果更为紧密；但对应的轮廓系数的值都比最大化轮廓系数小（这是必然的）。手肘法（以下特指版本2）得到的k值普遍比最大化轮廓系数法要大，原因可能在于轮廓系数的计算方式。轮廓系数考虑了分离度b和凝聚度a，如果分离度b和凝聚度a都比较大，但是b相对a大得多，此时就会得到一个较高的轮廓系数值。因此，轮廓系数虽然引入了分离度使两个簇尽可能分开，但也可能带来较大的SSE，使簇内分布较散。

从聚类的外部评估指标来看，首先是k值，手肘法在四个实验中得到的最优k值都刚好匹配真实类别数，说明手肘法是可靠的。接着，手肘法在4个数据集上都能取得较高的V-measure，调整兰德系数（ARI）和调整互信息（AMI）值，进一步说明本文提出的方法的有效性。

6. 总结

kmeans聚类算法的最优k值选取问题一直困扰着人们。本文提出了手肘法选取最优k值的改进版本，将手肘法寻找最优k值的过程自动化，不再依赖于人的经验判断，提高了决策的科学性。

但其实看本质的话，无论是手肘法还是最大化轮廓系数法，其本质都是一种经验主义的方法，即多次试验，然后从中选一个表现最好的。这存在一个明显的缺点，计算量大，如果数据量小还好，一旦数据量大起来这种经验主义的方法计算起来会比较耗时。其他聚类算法，如ISODATA、层次聚类、DBSCAN等，则没有确定聚类个数的困扰，但也有超参数不好确定的烦恼。

以上仅为我的一点思考，并没有严格的数学证明，大家如有更好的想法欢迎在评论区讨论。另外，版权所有，盗版必究。

参考资料
[1] [skearn官方文档] (https://scikit-learn.org/stable/modules/clustering.html#k-means)
[2] 《百面机器学习》, 诸葛越.
[3] http://c.biancheng.net/view/3708.html
[4] https://zhuanlan.zhihu.com/p/184686598
[5] https://blog.csdn.net/u010159842/article/details/78624135
[6] https://zhuanlan.zhihu.com/p/96081088
[6] https://blog.csdn.net/qq_16633405/article/details/119995976
[7] https://gdcoder.com/silhouette-analysis-vs-elbow-method-vs-davies-bouldin-index-selecting-the-optimal-number-of-clusters-for-kmeans-clustering/
[8] https://python-bloggers.com/2021/06/davies-bouldin-index-for-k-means-clustering-evaluation-in-python/
[9] https://blog.csdn.net/harry_128/article/details/80523568
[10] https://zhuanlan.zhihu.com/p/343667804
[11] https://sklearn.apachecn.org/#/docs/master/22