题目：124. 二叉树中的最大路径和

难度：困难

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

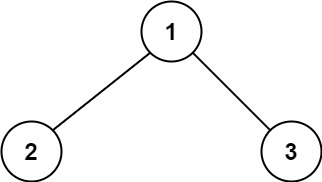
示例 1：

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

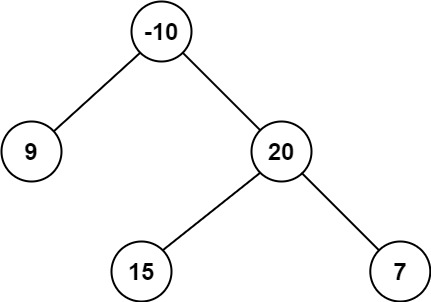
示例 2：

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

• 树中节点数目范围是 [1, 3 * 104]
• -1000 <= Node.val <= 1000

一、模式识别

可能穿过父节点 》 后序

最大路径和 》 哈希表记录 + 全局求最大值

二、代码实现

1.后序：迭代

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        ans = -inf
        records = defaultdict(int)
        stack, node, prev = [], root, None
        while stack or node:
            while node:
                stack.append(node)
                node = node.left
            node = stack.pop()
            if not node.right or node.right == prev:
                left = records[node.left]
                right = records[node.right]
                ans = max(ans, node.val + left + right)
                records[node] = max(node.val + left, node.val + right, 0)
                prev = node
                node = None
            else:
                stack.append(node)
                node = node.right
        return ans

2.后序：递归

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        ans = -inf
        
        def dfs(node):
            if not node: return 0
            left = max(dfs(node.left), 0)
            right = max(dfs(node.right), 0)
            nonlocal ans
            ans = max(ans, node.val + left + right)
            return node.val + max(left, right)
        
        dfs(root)
        return ans