由于CGAL整个源码和package的文档本身较多,涉及的第三方库和数学理论较多,所以会先对相关的Package的官网文档进行简要分析,之后对于源码进行分模块解析。
代数基础概念
参考以下博客:
c++基础概念
代数结构与特点
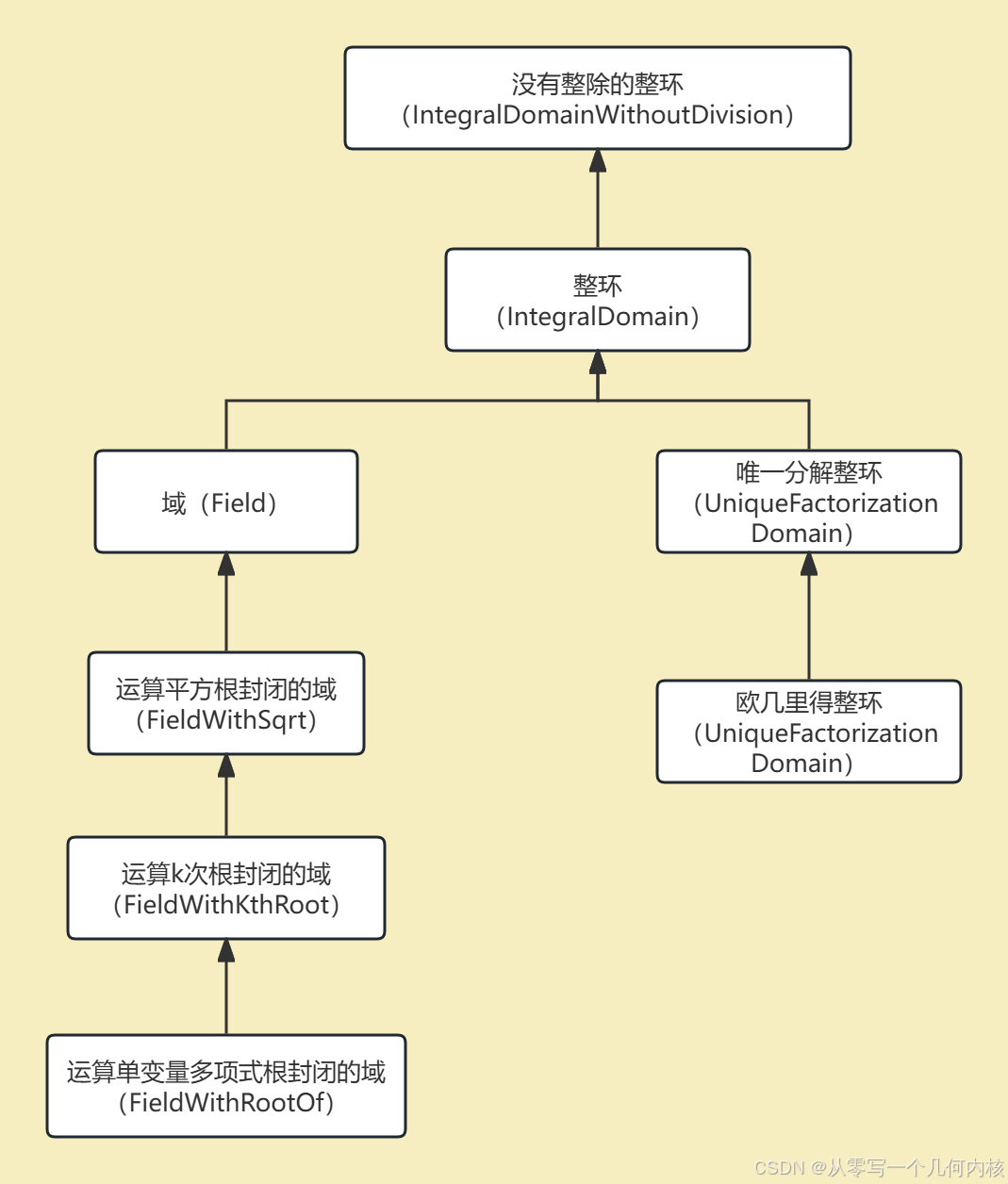
- FieldWithSqrt, FieldWithKthRoot and FieldWithRootOf 个人理解是:在运算"根号" " k次根"和"多项式的实根"下封闭的域。
- 源码片段
对于AS类型,Algebraic_structure_traits提供了几个标记。最重要的标记是Algebraic_category标记,它表示类型AS所实现的最精细的代数概念。如果类型不是代数结构概念的模型,甚至可以使用Null_tag。标签彼此派生,这样它们就反映了代数结构概念的层次结构,例如,Field_with_sqrt_tag派生Field_tag。源码片段:
//Algebraic_structure_traits<AS>中的标签struct
//! corresponds to the \c IntegralDomainWithoutDiv concept.
struct Integral_domain_without_division_tag {};
//! corresponds to the \c IntegralDomain concept.
struct Integral_domain_tag : public Integral_domain_without_division_tag {};
//! corresponds to the \c UFDomain concept.
struct Unique_factorization_domain_tag : public Integral_domain_tag {};
//! corresponds to the \c EuclideanRing concept.
struct Euclidean_ring_tag : public Unique_factorization_domain_tag {};
//! corresponds to the \c Field concept.
struct Field_tag : public Integral_domain_tag {};
//! corresponds to the \c FieldWithSqrt concept.
struct Field_with_sqrt_tag : public Field_tag {};
//! corresponds to the \c FieldWithKthRoot concept
struct Field_with_kth_root_tag : public Field_with_sqrt_tag {};
//! corresponds to the \c FieldWithRootOF concept.
struct Field_with_root_of_tag : public Field_with_kth_root_tag {};
// The algebraic structure traits template
// =========================================================================
template< class Type_ >
class Algebraic_structure_traits {
public:
typedef Type_ Type;
typedef Null_tag Algebraic_category;
typedef Null_tag Is_exact;
typedef Null_tag Is_numerical_sensitive;
typedef Null_functor Simplify;
typedef Null_functor Unit_part;
typedef Null_functor Integral_division;
typedef Null_functor Is_square;
typedef Null_functor Gcd;
typedef Null_functor Div_mod;
typedef Null_functor Div;
typedef Null_functor Mod;
typedef Null_functor Square;
typedef Null_functor Is_zero;
typedef Null_functor Is_one;
typedef Null_functor Sqrt;
typedef Null_functor Kth_root;
typedef Null_functor Root_of;
typedef Null_functor Divides;
typedef Null_functor Inverse;
};
// The algebraic structure traits base class
// =========================================================================
template< class Type, class Algebra_type >
class Algebraic_structure_traits_base;
//! The template specialization that can be used for types that are not any
//! of the number type concepts. All functors are set to \c Null_functor
//! or suitable defaults. The \c Simplify functor does nothing by default.
template< class Type_ >
class Algebraic_structure_traits_base< Type_, Null_tag > {
public:
typedef Type_ Type;
typedef Null_tag Algebraic_category;
typedef Tag_false Is_exact;
typedef Null_tag Is_numerical_sensitive;
typedef Null_tag Boolean;
// does nothing by default
class Simplify
: public CGAL::cpp98::unary_function< Type&, void > {
public:
void operator()( Type& ) const {}
};
typedef Null_functor Unit_part;
typedef Null_functor Integral_division;
typedef Null_functor Is_square;
typedef Null_functor Gcd;
typedef Null_functor Div_mod;
typedef Null_functor Div;
typedef Null_functor Mod;
typedef Null_functor Square;
typedef Null_functor Is_zero;
typedef Null_functor Is_one;
typedef Null_functor Sqrt;
typedef Null_functor Kth_root;
typedef Null_functor Root_of;
typedef Null_functor Divides;
typedef Null_functor Inverse;
};
//! The template specialization that is used if the number type is
//! a model of the \c IntegralDomainWithoutDiv concept. The \c Simplify
//! does nothing by default and the \c Unit_part is equal to
//! \c Type(-1) for negative numbers and
//! \c Type(1) otherwise
template< class Type_ >
class Algebraic_structure_traits_base< Type_,
Integral_domain_without_division_tag >
: public Algebraic_structure_traits_base< Type_,
Null_tag > {
public:
typedef Type_ Type;
typedef Integral_domain_without_division_tag Algebraic_category;
typedef bool Boolean;
// returns Type(1) by default
class Unit_part
: public CGAL::cpp98::unary_function< Type, Type > {
public:
Type operator()( const Type& x ) const {
return( x < Type(0)) ?
Type(-1) : Type(1);
}
};
class Square
: public CGAL::cpp98::unary_function< Type, Type > {
public:
Type operator()( const Type& x ) const {
return x*x;
}
};
class Is_zero
: public CGAL::cpp98::unary_function< Type, bool > {
public:
bool operator()( const Type& x ) const {
return x == Type(0);
}
};
class Is_one
: public CGAL::cpp98::unary_function< Type, bool > {
public:
bool operator()( const Type& x ) const {
return x == Type(1);
}
};
};
//! The template specialization that is used if the number type is
//! a model of the \c IntegralDomain concept. It is equivalent to the
//! specialization
//! for the \c IntegralDomainWithoutDiv concept. The additionally required
//! \c Integral_division functor needs to be implemented in the
//! \c Algebraic_structure_traits itself.
template< class Type_ >
class Algebraic_structure_traits_base< Type_,
Integral_domain_tag >
: public Algebraic_structure_traits_base< Type_,
Integral_domain_without_division_tag > {
public:
typedef Type_ Type;
typedef Integral_domain_tag Algebraic_category;
};
//! The template specialization that is used if the number type is
//! a model of the \c UFDomain concept. It is equivalent to the specialization
//! for the \c IntegralDomain concept. The additionally required
//! \c Integral_div functor
//! and \c Gcd functor need to be implemented in the
//! \c Algebraic_structure_traits itself.
template< class Type_ >
class Algebraic_structure_traits_base< Type_,
Unique_factorization_domain_tag >
: public Algebraic_structure_traits_base< Type_,
Integral_domain_tag > {
public:
typedef Type_ Type;
typedef Unique_factorization_domain_tag Algebraic_category;
// Default implementation of Divides functor for unique factorization domains
// x divides y if gcd(y,x) equals x up to inverses
class Divides
: public CGAL::cpp98::binary_function<Type,Type,bool>{
public:
bool operator()( const Type& x, const Type& y) const {
typedef CGAL::Algebraic_structure_traits<Type> AST;
typename AST::Gcd gcd;
typename AST::Unit_part unit_part;
typename AST::Integral_division idiv;
return gcd(y,x) == idiv(x,unit_part(x));
}
// second operator computing q = x/y
bool operator()( const Type& x, const Type& y, Type& q) const {
typedef CGAL::Algebraic_structure_traits<Type> AST;
typename AST::Integral_division idiv;
bool result = (*this)(x,y);
if( result == true )
q = idiv(x,y);
return result;
}
CGAL_IMPLICIT_INTEROPERABLE_BINARY_OPERATOR_WITH_RT(Type,bool)
};
};
- 精确与数字敏感
主要是处理浮点误差和类型溢出的问题,这个在计算的时候非常常见的问题。其中:Is_exact用来标记是否精确,Is_numerical_sensitive用来标记是否代数结构的性能对算法的条件数敏感。官网一个例子描述的很直白:
基本类型int对数字不敏感,但由于溢出而被认为是不精确的。相反,像leda_real或CORE::Expr这样的类型是精确的,但由于内部使用了多精度浮点运算,因此对数值问题很敏感。我们期望Is_numerical_sensitive用于算法调度,而Is_exact用于启用只能检查精确类型的断言。
- 可嵌入实轴
这块主要说的是数字类型是否表示实数的某个子集(类Real_embeddable_traits中Is_real_embeddable)。与Algebraic_structure代数结构正交设计。这样将类型与算术操作分离。如果类型是IntegralDomainWithoutDivision和RealEmbeddable的模型,则该类型的对象表示的数字对于算术和比较来说是相同的。由此可见,由这种类型表示的环是整数的超集和实数的子集,因此具有特征为零。如果类型是Field和RealEmbeddable的模型,则它是有理数的超集。
- 实数类型
每个CGAL内核(Kernel)都带有两个实数类型(可嵌入到实数中的数字类型)。其中一个是FieldNumberType,另一个是RingNumberType。基本核对象(点、向量等)的坐标来自这些类型之一(笛卡尔核FieldNumberType,齐次核RingNumberType)。概念FieldNumberType结合了概念Field和RealEmbeddable的定义,而RingNumberType结合了IntegralDomainWithoutDivision和RealEmbeddable的定义。
- 互操作性
就是混合类型运算进行类型判断并正确运算的。一般来说,混合操作由重载操作符和函数提供,或者仅通过隐式构造函数调用提供。这种级别的互操作性反映在ImplicitInteroperable这个概念上。然而,在模板代码中,混合算术运算的结果类型(即所谓的强制类型)可能不明确。因此,包引入了Coercion_traits,通过Coercion_traits<A,B>:: type访问两个可互操作类型A和B的强制类型。
一些简单的例子是强制类型为double的int和double,或者强制类型为Gmpq的Gmpz和Gmpq。然而,强制类型不一定是输入类型之一,例如,具有整数系数的多项式乘以有理类型的强制类型应该是具有有理系数的多项式。
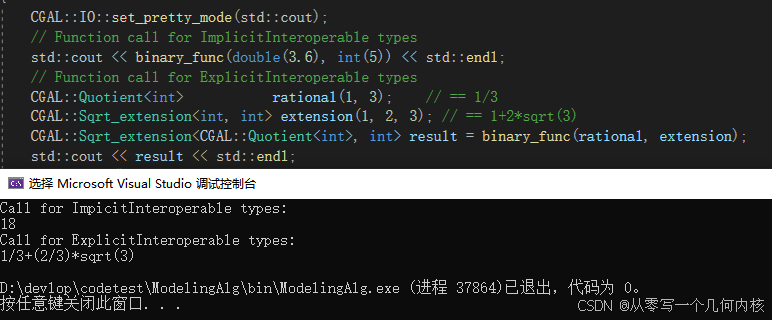
显示互操作例子:
// this is an implementation for ExplicitInteroperable types
// the result type is determined via Coercion_traits<A,B>
template <typename A, typename B>
typename CGAL::Coercion_traits<A,B>::Type
binary_func(const A& a , const B& b){
typedef CGAL::Coercion_traits<A,B> CT;
// check for explicit interoperability
CGAL_static_assertion((CT::Are_explicit_interoperable::value));
// CT::Cast is used to to convert both types into the coercion type
typename CT::Cast cast;
// all operations are performed in the coercion type
return cast(a)*cast(b);
}
隐式互操作例子:
// this is the implementation for ExplicitInteroperable types
template <typename A, typename B>
typename CGAL::Coercion_traits<A, B>::Type
binary_function_(const A& a, const B& b, CGAL::Tag_false) {
std::cout << "Call for ExplicitInteroperable types: " << std::endl;
typedef CGAL::Coercion_traits<A, B> CT;
typename CT::Cast cast;
return cast(a) * cast(b);
}
// this is the implementation for ImplicitInteroperable types
template <typename A, typename B>
typename CGAL::Coercion_traits<A, B>::Type
binary_function_(const A& a, const B& b, CGAL::Tag_true) {
std::cout << "Call for ImpicitInteroperable types: " << std::endl;
return a * b;
}
// this function selects the correct implementation
template <typename A, typename B>
typename CGAL::Coercion_traits<A, B>::Type
binary_func(const A& a, const B& b) {
typedef CGAL::Coercion_traits<A, B> CT;
//关键在Are_implicit_interoperable标识上
typedef typename CT::Are_implicit_interoperable Are_implicit_interoperable;
return binary_function_(a, b, Are_implicit_interoperable());
}
- 分数
有一些数字类型,人们希望将其分解为分子和分母。这不仅适用于像Quotient(商), Gmpq, mpq_class或leda_rational这样的有理数,也适用于像Sqrt_extension或Polynomial这样的复合对象,它们可以分解成(标量)分母和具有更简单系数类型(例如整数而不是有理数)的复合分子。通常在这些无分母的倍数上可以更快地执行操作。如果类型是Fraction,那么相关的功能以及分子和分母类型都由Fraction_traits提供。特别是,Fraction_traits提供了一个可用于分派的标记Is_fraction。
其中涉及的GMP和number type部分后面会解析。这个固网例子说的是多项式系数:
#include <CGAL/Fraction_traits.h>
#include <CGAL/IO/io.h>
#include <vector>
#include <CGAL/number_utils.h>
template <class Fraction>
std::vector<typename CGAL::Fraction_traits<Fraction>::Numerator_type >
integralize(
const std::vector<Fraction>& vec,
typename CGAL::Fraction_traits<Fraction>::Denominator_type& d
) {
typedef CGAL::Fraction_traits<Fraction> FT;
typedef typename FT::Numerator_type Numerator_type;
typedef typename FT::Denominator_type Denominator_type;
typename FT::Decompose decompose;
std::vector<Numerator_type> num(vec.size());
std::vector<Denominator_type> den(vec.size());
// decompose each coefficient into integral part and denominator
for (unsigned int i = 0; i < vec.size(); i++) {
decompose(vec[i], num[i], den[i]);
}
// compute 'least' common multiple of all denominator
// We would like to use gcd, so let's think of Common_factor as gcd.
typename FT::Common_factor gcd;
d = 1;
for (unsigned int i = 0; i < vec.size(); i++) {
d *= CGAL::integral_division(den[i], gcd(d, den[i]));
}
// expand each (numerator, denominator) pair to common denominator
for (unsigned int i = 0; i < vec.size(); i++) {
// For simplicity ImplicitInteroperability is expected in this example
num[i] *= CGAL::integral_division(d, den[i]);
}
return num;
}
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpz.h>
#include <CGAL/Gmpq.h>
int main(){
std::vector<CGAL::Gmpq> vec(3);
vec[0]=CGAL::Gmpq(1,4);
vec[1]=CGAL::Gmpq(1,6);
vec[2]=CGAL::Gmpq(1,10);
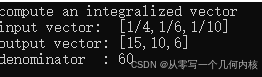
std::cout<< "compute an integralized vector" << std::endl;
std::cout<<"input vector: ["
<< vec[0] << "," << vec[1] << "," << vec[2] << "]" << std::endl;
CGAL::Gmpz d;
std::vector<CGAL::Gmpz> integral_vec = integralize(vec,d);
std::cout<<"output vector: ["
<< integral_vec[0] << ","
<< integral_vec[1] << ","
<< integral_vec[2] << "]" << std::endl;
std::cout<<"denominator : "<< d <<std::endl;
}
#else
int main(){ std::cout << "This examples needs GMP" << std::endl; }
#endif