1. 缩放变换
1.1. 缩放变换的数学原理
缩放变换可以用矩阵乘法表示:
( k 1 0 0 k 2 ) ( x y ) = ( k 1 x k 2 y ) \begin{pmatrix} k_1 & 0 \\ 0 & k_2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} k_1x \\ k_2y \end{pmatrix} (k100k2)(xy)=(k1xk2y)
其中:
- k 1 k_1 k1 是 x 方向的缩放因子
- k 2 k_2 k2 是 y 方向的缩放因子
让我创建一个可视化来展示这个变换的效果。
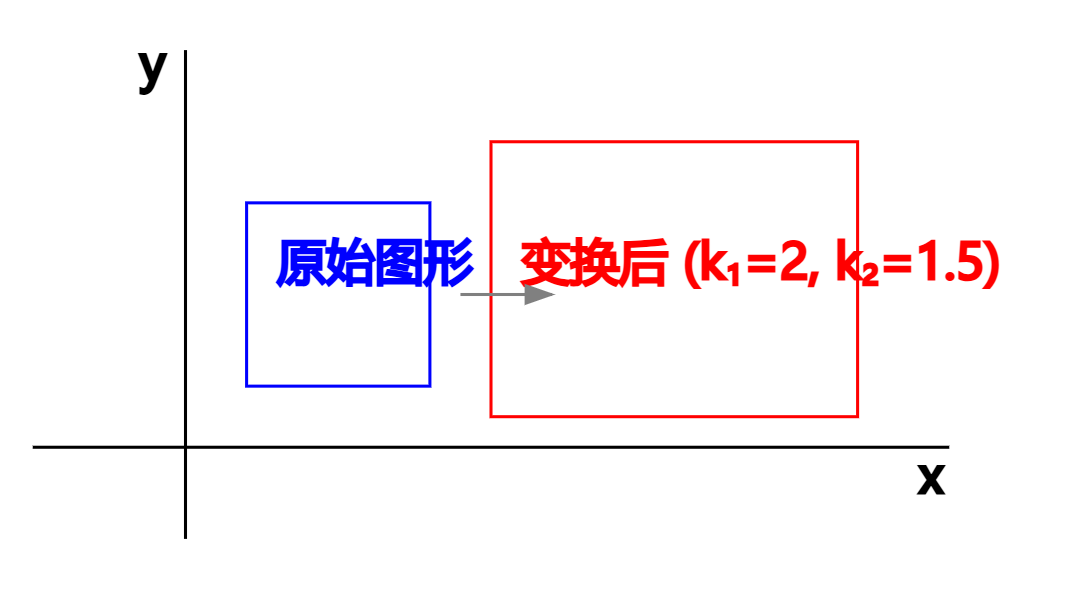
缩放变换的效果解析
在上图中,我展示了一个具体的例子:
- 蓝色方框是原始图形,坐标为 ( x , y ) (x,y) (x,y)
- 红色方框是变换后的图形,其中:
- x 方向缩放因子 k 1 = 2 k_1=2 k1=2 (宽度变为原来的2倍)
- y 方向缩放因子 k 2 = 1.5 k_2=1.5 k2=1.5 (高度变为原来的1.5倍)
当应用变换时,原始坐标 ( x , y ) (x,y) (x,y) 变为 ( k 1 x , k 2 y ) (k_1x,k_2y) (k1x,k2y)。这意味着:
- x 坐标被乘以 k 1 k_1 k1
- y 坐标被乘以 k 2 k_2 k2
特殊情况:
- 当 k 1 = k 2 k_1 = k_2 k1=k2 时,图形会均匀缩放
- 当 k 1 ≠ k 2 k_1 \neq k_2 k1=k2 时,图形会产生非均匀缩放,可能改变原始图形的比例
- 当 0 < k < 1 0 < k < 1 0<k<1 时表示缩小
- 当 k > 1 k > 1 k>1 时表示放大
1.2. 缩放变换的具体例子
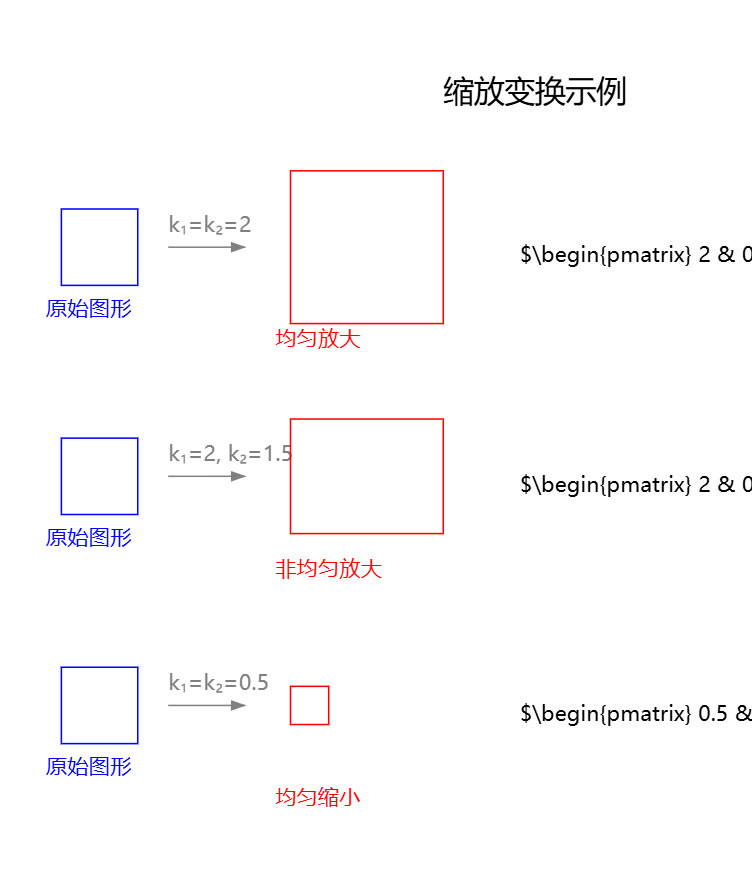
1. 均匀放大 ( k 1 = k 2 = 2 k_1=k_2=2 k1=k2=2)
当缩放系数相等且大于1时,图形会保持原有比例放大:
- 原坐标 ( x , y ) (x,y) (x,y) 变换为 ( 2 x , 2 y ) (2x,2y) (2x,2y)
- 面积增大为原来的4倍
- 形状保持不变,只是尺寸变大
2. 非均匀放大 ( k 1 = 2 , k 2 = 1.5 k_1=2, k_2=1.5 k1=2,k2=1.5)
当 k 1 ≠ k 2 k_1 \neq k_2 k1=k2 时,图形会发生形变:
- x方向放大2倍
- y方向放大1.5倍
- 最终形状变为矩形
- 原有的长宽比发生改变
3. 均匀缩小 ( k 1 = k 2 = 0.5 k_1=k_2=0.5 k1=k2=0.5)
当缩放系数相等且小于1时,图形会保持原有比例缩小:
- 原坐标 ( x , y ) (x,y) (x,y) 变换为 ( 0.5 x , 0.5 y ) (0.5x,0.5y) (0.5x,0.5y)
- 面积减小为原来的0.25倍
- 形状保持不变,只是尺寸变小
这些变换都可以用矩阵乘法表示:
( k 1 0 0 k 2 ) ( x y ) = ( k 1 x k 2 y ) \begin{pmatrix} k_1 & 0 \\ 0 & k_2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} k_1x \\ k_2y \end{pmatrix} (k100k2)(xy)=(k1xk2y)
其中 k 1 k_1 k1 和 k 2 k_2 k2 的不同取值会产生不同的缩放效果。
3. 缩放变换在机器学习的使用场景
1. 数据预处理中的特征缩放
在机器学习中,最基础的应用是特征缩放:
x s c a l e d = x − x m i n x m a x − x m i n x_{scaled} = \frac{x - x_{min}}{x_{max} - x_{min}} xscaled=xmax−xminx−xmin
这实际上是一种线性变换,可以用矩阵形式表示:
( 1 x m a x − x m i n 0 0 1 y m a x − y m i n ) ( x − x m i n y − y m i n ) \begin{pmatrix} \frac{1}{x_{max} - x_{min}} & 0 \\ 0 & \frac{1}{y_{max} - y_{min}} \end{pmatrix} \begin{pmatrix} x - x_{min} \\ y - y_{min} \end{pmatrix} (xmax−xmin100ymax−ymin1)(x−xminy−ymin)
2. 计算机视觉应用
- 图像预处理
- 输入图像缩放到统一尺寸:
( t a r g e t _ w i d t h o r i g i n a l _ w i d t h 0 0 t a r g e t _ h e i g h t o r i g i n a l _ h e i g h t ) \begin{pmatrix} \frac{target\_width}{original\_width} & 0 \\ 0 & \frac{target\_height}{original\_height} \end{pmatrix} (original_widthtarget_width00original_heighttarget_height)
- 数据增强 (Data Augmentation)
- 随机缩放作为增强策略:
( k 1 0 0 k 2 ) , 其中 k 1 , k 2 ∈ [ 0.8 , 1.2 ] \begin{pmatrix} k_1 & 0 \\ 0 & k_2 \end{pmatrix}, \text{其中} k_1,k_2 \in [0.8, 1.2] (k100k2),其中k1,k2∈[0.8,1.2]
3. 深度学习中的应用
- 特征图(Feature Map)缩放
- 在卷积神经网络中缩放特征图尺寸:
output_size = ( 1 s t r i d e _ x 0 0 1 s t r i d e _ y ) ( i n p u t _ w i d t h i n p u t _ h e i g h t ) \text{output\_size} = \begin{pmatrix} \frac{1}{stride\_x} & 0 \\ 0 & \frac{1}{stride\_y} \end{pmatrix} \begin{pmatrix} input\_width \\ input\_height \end{pmatrix} output_size=(stride_x100stride_y1)(input_widthinput_height)
- 学习率调整
- 学习率随时间的动态缩放:
l r t = l r 0 ⋅ ( d e c a y _ r a t e t 0 0 d e c a y _ r a t e t ) lr_t = lr_0 \cdot \begin{pmatrix} decay\_rate^t & 0 \\ 0 & decay\_rate^t \end{pmatrix} lrt=lr0⋅(decay_ratet00decay_ratet)
4. 推荐系统
-
用户-物品评分矩阵归一化
r a t i n g n o r m a l i z e d = r a t i n g − r a t i n g m i n r a t i n g m a x − r a t i n g m i n rating_{normalized} = \frac{rating - rating_{min}}{rating_{max} - rating_{min}} ratingnormalized=ratingmax−ratingminrating−ratingmin -
特征向量缩放
- 将不同尺度的特征统一到相同范围:
( 1 σ 1 0 0 1 σ 2 ) ( x 1 − μ 1 x 2 − μ 2 ) \begin{pmatrix} \frac{1}{\sigma_1} & 0 \\ 0 & \frac{1}{\sigma_2} \end{pmatrix} \begin{pmatrix} x_1 - \mu_1 \\ x_2 - \mu_2 \end{pmatrix} (σ1100σ21)(x1−μ1x2−μ2)
5. 实际应用注意事项
- 训练集和测试集使用相同的缩放参数
- 处理异常值和边界情况
- 选择合适的缩放方法(Min-Max、StandardScaler等)
- 考虑特征的物理意义
缩放变换在机器学习中的应用非常广泛,它不仅能提高模型的训练效率,还能改善模型的性能和泛化能力。选择合适的缩放策略对模型的最终效果有重要影响。
4. 缩放变换习题
习题1: 基础坐标变换
题目:
点
P
(
2
,
3
)
P(2,3)
P(2,3) 经过缩放变换矩阵
(
2
0
0
3
)
\begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}
(2003) 后的新坐标是什么?
解答:
让我们逐步解决:
-
使用矩阵乘法计算:
( 2 0 0 3 ) ( 2 3 ) = ( 2 ⋅ 2 3 ⋅ 3 ) = ( 4 9 ) \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 2 \cdot 2 \\ 3 \cdot 3 \end{pmatrix} = \begin{pmatrix} 4 \\ 9 \end{pmatrix} (2003)(23)=(2⋅23⋅3)=(49) -
因此,点P变换后的新坐标为 ( 4 , 9 ) (4,9) (4,9)
习题2: 面积变化计算
题目:
一个正方形的边长为2,经过缩放变换矩阵
(
3
0
0
2
)
\begin{pmatrix} 3 & 0 \\ 0 & 2 \end{pmatrix}
(3002) 后,求变换后图形的面积。
解答:
-
原正方形的面积:
- A 原 = 2 × 2 = 4 A_{原} = 2 \times 2 = 4 A原=2×2=4 平方单位
-
缩放变换的影响:
- x方向放大3倍:新宽度 = 2 × 3 = 6 2 \times 3 = 6 2×3=6
- y方向放大2倍:新高度 = 2 × 2 = 4 2 \times 2 = 4 2×2=4
-
变换后的面积:
- A 新 = 6 × 4 = 24 A_{新} = 6 \times 4 = 24 A新=6×4=24 平方单位
- 也可以理解为: A 新 = A 原 × ∣ d e t ( M ) ∣ A_{新} = A_{原} \times |det(M)| A新=A原×∣det(M)∣
- 其中 d e t ( M ) = ∣ 3 0 0 2 ∣ = 6 det(M) = \begin{vmatrix} 3 & 0 \\ 0 & 2 \end{vmatrix} = 6 det(M)= 3002 =6
- 所以 A 新 = 4 × 6 = 24 A_{新} = 4 \times 6 = 24 A新=4×6=24
习题3: 机器学习应用
题目:
在机器学习中,有一组年龄数据
[
25
,
35
,
45
,
55
]
[25, 35, 45, 55]
[25,35,45,55],要求将其归一化到
[
0
,
1
]
[0,1]
[0,1] 范围。使用 Min-Max 缩放方法计算结果。
解答:
-
Min-Max 缩放公式:
x s c a l e d = x − x m i n x m a x − x m i n x_{scaled} = \frac{x - x_{min}}{x_{max} - x_{min}} xscaled=xmax−xminx−xmin -
找出数据的最大值和最小值:
- x m i n = 25 x_{min} = 25 xmin=25
- x m a x = 55 x_{max} = 55 xmax=55
- 范围 = 55 − 25 = 30 55 - 25 = 30 55−25=30
-
对每个数据点进行转换:
- 对于 25: 25 − 25 30 = 0 \frac{25-25}{30} = 0 3025−25=0
- 对于 35: 35 − 25 30 = 0.33 \frac{35-25}{30} = 0.33 3035−25=0.33
- 对于 45: 45 − 25 30 = 0.67 \frac{45-25}{30} = 0.67 3045−25=0.67
- 对于 55: 55 − 25 30 = 1 \frac{55-25}{30} = 1 3055−25=1
所以归一化后的结果是: [ 0 , 0.33 , 0.67 , 1 ] [0, 0.33, 0.67, 1] [0,0.33,0.67,1]
这些习题涵盖了缩放变换的基本计算、几何意义和实际应用,有助于深入理解缩放变换的概念和应用。
5. 项目中,这个缩放矩阵是如何确定的?
1. 项目一: 图像
在3D图形编程中,缩放矩阵是一个4×4的矩阵,用于对物体进行缩放变换。基本的缩放矩阵形式如下:
S = [ s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ] S = \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} S= sx0000sy0000sz00001
其中:
- s x s_x sx 表示在x轴方向的缩放因子
- s y s_y sy 表示在y轴方向的缩放因子
- s z s_z sz 表示在z轴方向的缩放因子
当这个矩阵与一个点 P ( x , y , z , 1 ) P(x,y,z,1) P(x,y,z,1) 相乘时,得到新的坐标:
[ s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ] [ x y z 1 ] = [ s x x s y y s z z 1 ] \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} s_x x \\ s_y y \\ s_z z \\ 1 \end{bmatrix} sx0000sy0000sz00001 xyz1 = sxxsyyszz1
缩放因子的确定通常基于以下几个方面:
-
均匀缩放:当 s x = s y = s z = s s_x = s_y = s_z = s sx=sy=sz=s 时,物体在所有方向上等比例缩放
-
非均匀缩放:当 s x ≠ s y ≠ s z s_x \neq s_y \neq s_z sx=sy=sz 时,物体在不同方向上有不同的缩放比例
-
特殊情况:
- 当 s > 1 s > 1 s>1 时表示放大
- 当 0 < s < 1 0 < s < 1 0<s<1 时表示缩小
- 当 s = 1 s = 1 s=1 时表示保持原始大小
- 当 s < 0 s < 0 s<0 时表示镜像反射
在实际项目中,缩放因子可以通过以下方式确定:
-
基于屏幕分辨率的自适应缩放:
s = 实际屏幕分辨率 设计分辨率 s = \frac{实际屏幕分辨率}{设计分辨率} s=设计分辨率实际屏幕分辨率 -
基于视距的动态缩放:
s = 参考距离 当前视距 s = \frac{参考距离}{当前视距} s=当前视距参考距离 -
基于目标尺寸的精确缩放:
s = 目标尺寸 当前尺寸 s = \frac{目标尺寸}{当前尺寸} s=当前尺寸目标尺寸
这些公式会根据具体的应用场景和需求来选择使用。
2. 项目2: 特征缩放的数学原理
我来解释在机器学习中的特征缩放(Feature Scaling),并结合可视化来说明其重要性。
特征缩放的数学原理
在机器学习中,特征缩放主要有两种常用方法:
-
Min-Max缩放(归一化):将数据缩放到[0,1]区间
X n o r m = X − X m i n X m a x − X m i n X_{norm} = \frac{X - X_{min}}{X_{max} - X_{min}} Xnorm=Xmax−XminX−Xmin -
标准化(Z-score标准化):将数据转换为均值为0,标准差为1的分布
X s t d = X − μ σ X_{std} = \frac{X - \mu}{\sigma} Xstd=σX−μ
其中:
- X X X 是原始值
- μ \mu μ 是平均值
- σ \sigma σ 是标准差
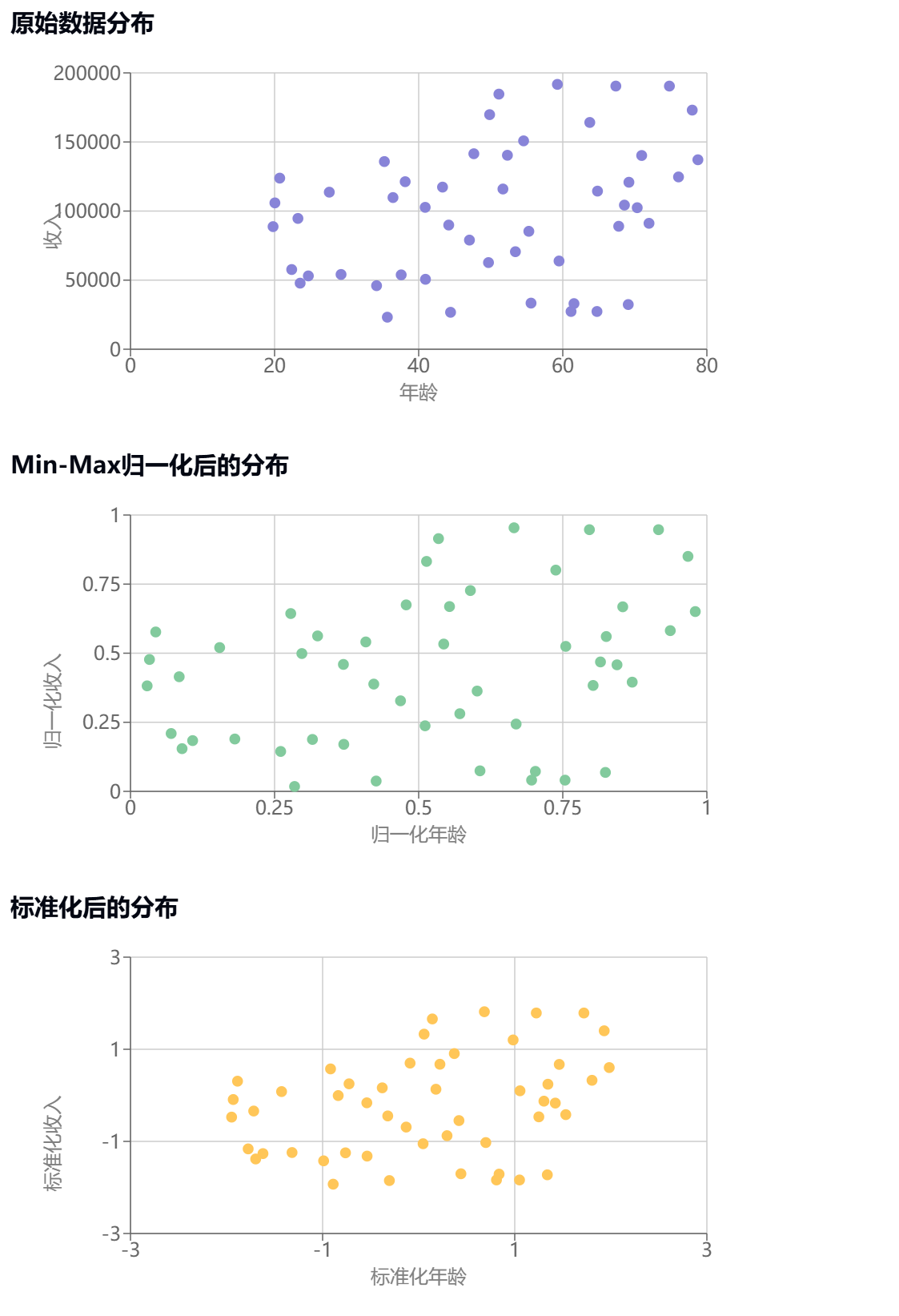
让我们通过一个具体的数据可视化例子来说明特征缩放的效果:
为什么需要特征缩放?
-
梯度下降收敛更快
当特征的尺度不同时,损失函数的等高线会呈现椭圆形,这会导致梯度下降路径呈"之"字形,收敛较慢。经过特征缩放后,等高线会更接近圆形,使得梯度下降能更直接地到达最优点。 -
避免特征主导
以上图为例,在原始数据中,收入的数值范围(20000-200000)远大于年龄范围(18-80),这会导致:- 在计算距离时,收入特征会主导结果
- 在权重更新时,收入特征的梯度会比年龄特征大得多
-
提高数值稳定性
某些算法(如Neural Networks)在数值较大时可能出现数值不稳定的情况。通过特征缩放,可以:- 避免梯度爆炸或消失
- 提高计算精度
- 加快训练速度
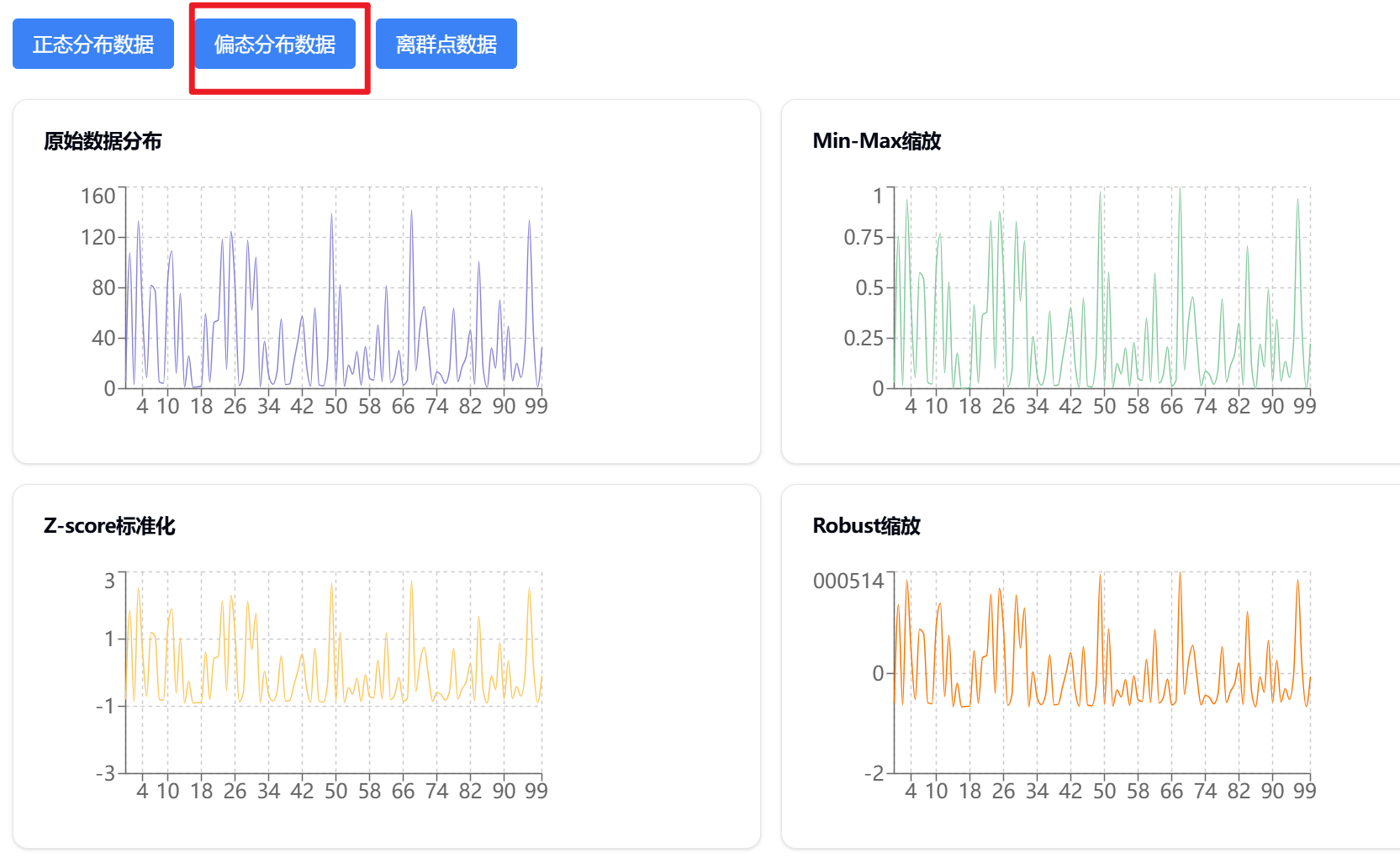
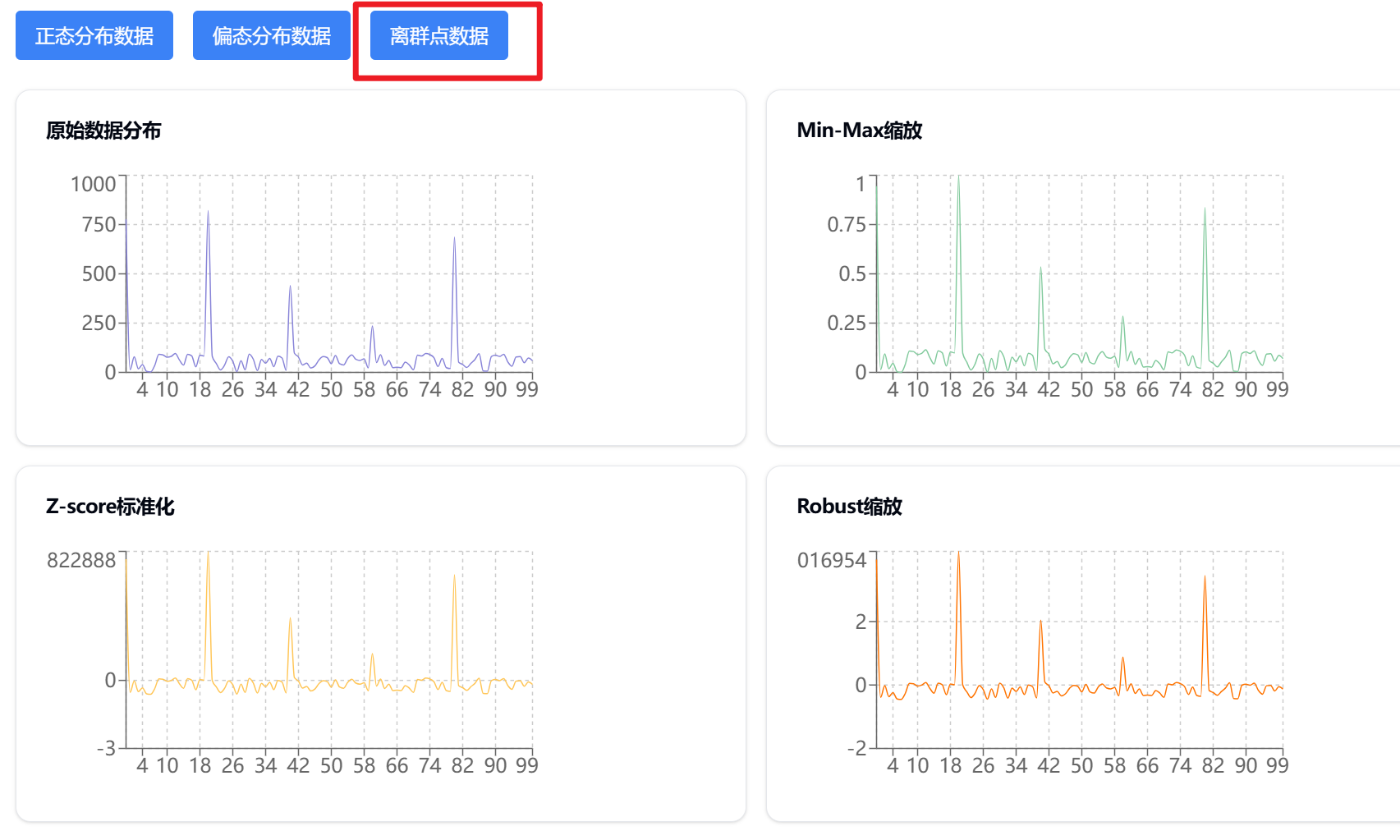
何时使用不同的缩放方法?
-
Min-Max归一化 适用于:
- 需要将特征限制在固定范围内
- 数据分布不是正态分布
- 数据中有离群点,但我们不想完全消除其影响
-
标准化 适用于:
- 数据近似正态分布
- 需要处理离群点
- 使用基于距离的算法(如SVM、KNN)
观察上面的可视化图表,我们可以看到:
- 原始数据中,两个特征的尺度差异很大
- Min-Max归一化后,所有数据都被压缩到[0,1]区间
- 标准化后,数据主要分布在[-3,3]区间,均值接近0
这种可视化有助于我们理解不同缩放方法对数据分布的影响,从而选择合适的缩放方法。
3. 项目3: 特征缩放矩阵确定
基本缩放矩阵结构
对于n个特征的数据,缩放矩阵 S S S 是一个 n × n n \times n n×n 的对角矩阵:
S = [ s 1 0 ⋯ 0 0 s 2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ s n ] S = \begin{bmatrix} s_1 & 0 & \cdots & 0 \\ 0 & s_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & s_n \end{bmatrix} S= s10⋮00s2⋮0⋯⋯⋱⋯00⋮sn
让我们通过一个可视化示例来展示缩放矩阵的确定和应用过程:
缩放矩阵的确定步骤
- Min-Max缩放矩阵
对于每个特征 i i i,缩放系数计算如下:
s i = 1 x m a x ( i ) − x m i n ( i ) s_i = \frac{1}{x_{max}^{(i)} - x_{min}^{(i)}} si=xmax(i)−xmin(i)1
变换过程:
x
s
c
a
l
e
d
(
i
)
=
s
i
(
x
(
i
)
−
x
m
i
n
(
i
)
)
x_{scaled}^{(i)} = s_i(x^{(i)} - x_{min}^{(i)})
xscaled(i)=si(x(i)−xmin(i))
完整的变换方程:
[ x s c a l e d ( 1 ) x s c a l e d ( 2 ) ⋮ x s c a l e d ( n ) ] = [ s 1 0 ⋯ 0 0 s 2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ s n ] [ x ( 1 ) − x m i n ( 1 ) x ( 2 ) − x m i n ( 2 ) ⋮ x ( n ) − x m i n ( n ) ] \begin{bmatrix} x_{scaled}^{(1)} \\ x_{scaled}^{(2)} \\ \vdots \\ x_{scaled}^{(n)} \end{bmatrix} = \begin{bmatrix} s_1 & 0 & \cdots & 0 \\ 0 & s_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & s_n \end{bmatrix} \begin{bmatrix} x^{(1)} - x_{min}^{(1)} \\ x^{(2)} - x_{min}^{(2)} \\ \vdots \\ x^{(n)} - x_{min}^{(n)} \end{bmatrix} xscaled(1)xscaled(2)⋮xscaled(n) = s10⋮00s2⋮0⋯⋯⋱⋯00⋮sn x(1)−xmin(1)x(2)−xmin(2)⋮x(n)−xmin(n)
- 标准化缩放矩阵
对于每个特征 i i i,缩放系数为:
s i = 1 σ ( i ) s_i = \frac{1}{\sigma^{(i)}} si=σ(i)1
其中 σ ( i ) \sigma^{(i)} σ(i) 是第 i i i 个特征的标准差。
变换方程:
[ x s t d ( 1 ) x s t d ( 2 ) ⋮ x s t d ( n ) ] = [ s 1 0 ⋯ 0 0 s 2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ s n ] [ x ( 1 ) − μ ( 1 ) x ( 2 ) − μ ( 2 ) ⋮ x ( n ) − μ ( n ) ] \begin{bmatrix} x_{std}^{(1)} \\ x_{std}^{(2)} \\ \vdots \\ x_{std}^{(n)} \end{bmatrix} = \begin{bmatrix} s_1 & 0 & \cdots & 0 \\ 0 & s_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & s_n \end{bmatrix} \begin{bmatrix} x^{(1)} - \mu^{(1)} \\ x^{(2)} - \mu^{(2)} \\ \vdots \\ x^{(n)} - \mu^{(n)} \end{bmatrix} xstd(1)xstd(2)⋮xstd(n) = s10⋮00s2⋮0⋯⋯⋱⋯00⋮sn x(1)−μ(1)x(2)−μ(2)⋮x(n)−μ(n)
实际应用注意事项
-
数据预处理
- 在确定缩放矩阵前,需要处理缺失值和异常值
- 计算统计量(最大值、最小值、均值、标准差)时应使用训练集数据
-
缩放矩阵的保存
- 需要保存训练集上计算的缩放参数
- 对测试集使用相同的缩放参数
-
特征相关性考虑
- 如果特征间存在强相关性,可能需要考虑使用PCA等降维方法
- 在这种情况下,缩放矩阵会变成完整的变换矩阵,不再是对角矩阵
-
数值稳定性
- 需要注意特征值过小或过大的情况
- 可能需要添加小的常数项避免除零错误
以上可视化展示了原始数据和应用缩放矩阵后的数据分布。我们可以清楚地看到,通过适当的缩放矩阵,数据被转换到了相似的尺度范围内,这对后续的机器学习算法非常有帮助。
6. 项目中,使用缩放矩阵的思路和技巧
我来分享在项目中使用缩放矩阵的具体实践思路和技巧。
- 缩放矩阵选择的思路
让我创建一个可视化组件来展示不同场景下的缩放策略:
- 实践技巧
以下是在项目中使用缩放矩阵的关键技巧:
a) 数据分析阶段
def analyze_feature_distribution(feature_data):
# 计算基本统计量
stats = {
'mean': np.mean(feature_data),
'std': np.std(feature_data),
'skewness': stats.skew(feature_data),
'kurtosis': stats.kurtosis(feature_data)
}
return stats
b) 缩放矩阵实现
class ScalingMatrix:
def __init__(self, method='minmax'):
self.method = method
self.params = {}
def fit(self, X):
if self.method == 'minmax':
self.params['min'] = X.min(axis=0)
self.params['max'] = X.max(axis=0)
self.scaling_matrix = np.diag(1 / (self.params['max'] - self.params['min']))
elif self.method == 'standard':
self.params['mean'] = X.mean(axis=0)
self.params['std'] = X.std(axis=0)
self.scaling_matrix = np.diag(1 / self.params['std'])
def transform(self, X):
if self.method == 'minmax':
return np.dot(X - self.params['min'], self.scaling_matrix)
elif self.method == 'standard':
return np.dot(X - self.params['mean'], self.scaling_matrix)
- 应用场景的选择
a) Min-Max缩放适用场景:
- 图像处理(像素值归一化)
- 神经网络的输入层
- 需要非负值的算法
示例代码:
def apply_minmax_scaling(image_data):
scaling_matrix = np.diag([1/255, 1/255, 1/255]) # RGB channels
return np.dot(image_data, scaling_matrix)
b) 标准化缩放适用场景:
- 基于距离的算法(如KNN、K-means)
- 需要处理异常值
- 特征有显著的尺度差异
def apply_standard_scaling(features):
mean = features.mean(axis=0)
std = features.std(axis=0)
scaling_matrix = np.diag(1/std)
return np.dot(features - mean, scaling_matrix)
- 优化技巧
a) 稀疏矩阵优化:
from scipy.sparse import diags
def create_sparse_scaling_matrix(scale_factors):
return diags(scale_factors, 0)
b) 数值稳定性处理:
def create_stable_scaling_matrix(scale_factors, epsilon=1e-7):
# 避免除零
stable_factors = 1 / (np.abs(scale_factors) + epsilon)
return np.diag(stable_factors)
- 实时更新策略
class OnlineScalingMatrix:
def __init__(self, n_features):
self.n = 0
self.mean = np.zeros(n_features)
self.M2 = np.zeros(n_features)
def update(self, x):
self.n += 1
delta = x - self.mean
self.mean += delta / self.n
delta2 = x - self.mean
self.M2 += delta * delta2
@property
def scaling_matrix(self):
variance = self.M2 / (self.n - 1)
return np.diag(1 / np.sqrt(variance))
- 性能监控
def monitor_scaling_impact(X, y, model, scaler):
# 记录缩放前的性能
base_score = model.score(X, y)
# 应用缩放
X_scaled = scaler.transform(X)
scaled_score = model.score(X_scaled, y)
return {
'improvement': scaled_score - base_score,
'scaling_condition_number': np.linalg.cond(scaler.scaling_matrix)
}
通过上面的可视化和代码示例,我们可以看到不同缩放策略在不同数据分布下的效果。在实际项目中,建议:
- 先进行数据分布分析
- 根据数据特点选择合适的缩放策略
- 使用适当的矩阵实现方式
- 注意数值稳定性
- 建立性能监控机制
这样可以确保缩放矩阵在项目中发挥最佳效果。
7. 缩放矩阵综合实战
7.1 案例背景
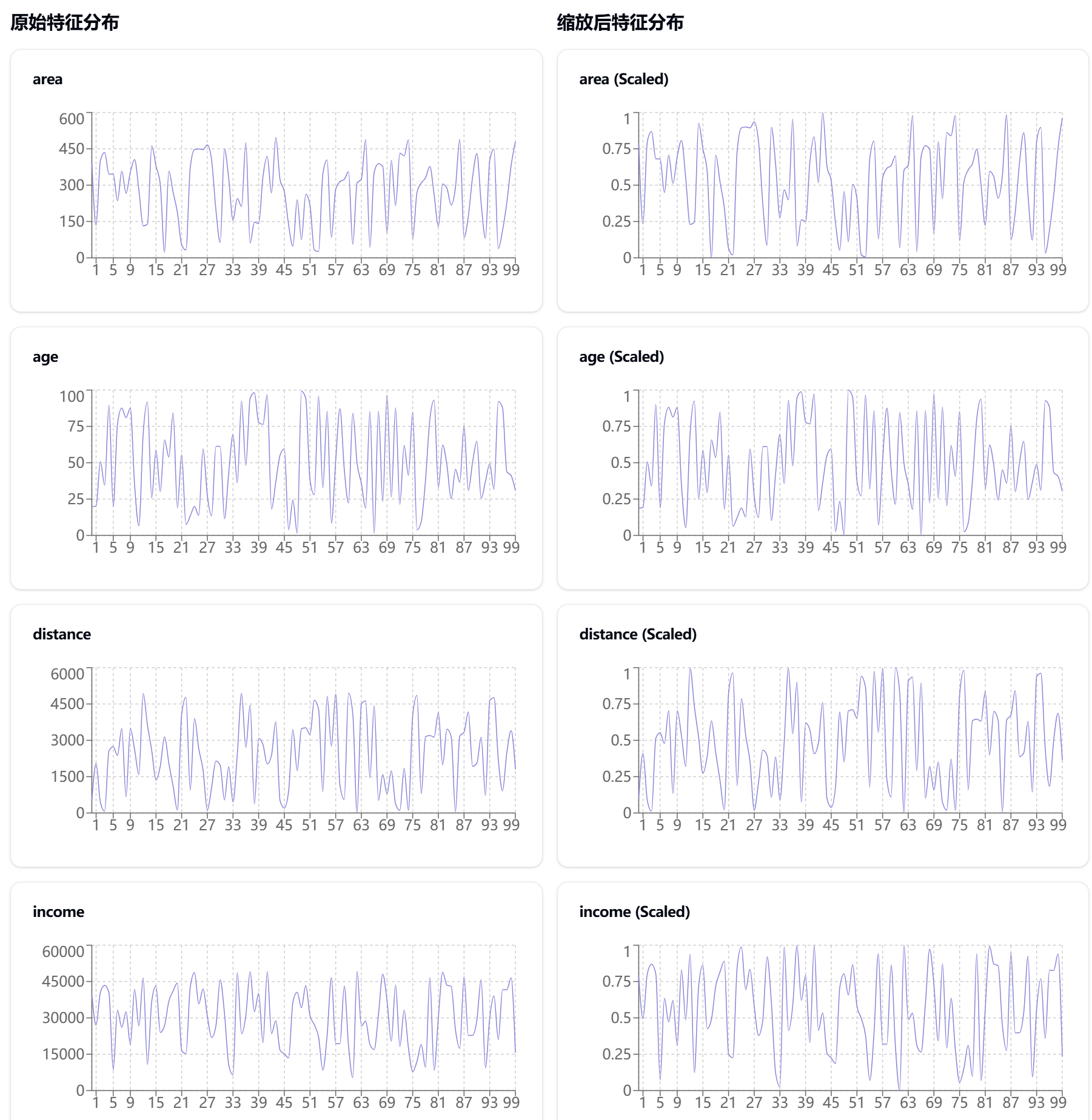
假设我们正在开发一个房地产价格预测系统,数据包含以下特征:
- 房屋面积(20-500平方米)
- 房龄(0-100年)
- 距地铁距离(0-5000米)
- 月收入(5000-50000元)
- 房价(目标变量)
让我们通过可视化来展示这个案例:
7.2 为什么选用缩放矩阵
-
特征尺度差异显著
- 面积:20-500平方米
- 距离:0-5000米
- 收入:5000-50000元
这些特征的量级差异巨大,需要统一尺度。
-
模型要求
- 使用梯度下降的模型(如神经网络)对特征尺度敏感
- 基于距离的算法(如KNN)需要特征在相似尺度
-
数值计算考虑
- 避免大数值造成的数值不稳定性
- 提高计算精度和收敛速度
7.3 缩放矩阵使用思路和技巧
class RealEstateScaling:
def __init__(self):
self.scaling_matrices = {}
self.feature_stats = {}
def analyze_features(self, X):
"""分析特征分布"""
feature_stats = {}
for feature in X.columns:
stats = {
'min': X[feature].min(),
'max': X[feature].max(),
'mean': X[feature].mean(),
'std': X[feature].std(),
'skew': X[feature].skew()
}
feature_stats[feature] = stats
return feature_stats
def determine_scaling_strategy(self, feature_stats):
"""确定每个特征的缩放策略"""
strategies = {}
for feature, stats in feature_stats.items():
if abs(stats['skew']) > 1.5:
strategies[feature] = 'robust'
elif stats['max'] / stats['min'] > 1000:
strategies[feature] = 'log'
else:
strategies[feature] = 'minmax'
return strategies
def create_scaling_matrix(self, X, strategy):
"""创建缩放矩阵"""
n_features = X.shape[1]
scaling_matrix = np.eye(n_features)
for i, feature in enumerate(X.columns):
if strategy[feature] == 'minmax':
scaling_matrix[i,i] = 1 / (X[feature].max() - X[feature].min())
elif strategy[feature] == 'robust':
q75, q25 = np.percentile(X[feature], [75, 25])
iqr = q75 - q25
scaling_matrix[i,i] = 1 / iqr
elif strategy[feature] == 'log':
scaling_matrix[i,i] = 1 / np.log(X[feature].max())
return scaling_matrix
7.4 完整使用过程
- 数据预处理
def preprocess_data(df):
# 处理缺失值
df = df.fillna(df.mean())
# 检测并处理异常值
for feature in df.columns:
q1 = df[feature].quantile(0.25)
q3 = df[feature].quantile(0.75)
iqr = q3 - q1
df = df[
(df[feature] >= q1 - 1.5 * iqr) &
(df[feature] <= q3 + 1.5 * iqr)
]
return df
- 初始化缩放器
scaler = RealEstateScaling()
- 分析特征
feature_stats = scaler.analyze_features(X_train)
scaling_strategies = scaler.determine_scaling_strategy(feature_stats)
- 创建并应用缩放矩阵
scaling_matrix = scaler.create_scaling_matrix(X_train, scaling_strategies)
X_train_scaled = np.dot(X_train, scaling_matrix)
- 模型训练和评估
def train_and_evaluate(X_train, X_test, y_train, y_test, scaling_matrix):
# 应用缩放
X_train_scaled = np.dot(X_train, scaling_matrix)
X_test_scaled = np.dot(X_test, scaling_matrix)
# 训练模型
model = LGBMRegressor()
model.fit(X_train_scaled, y_train)
# 评估性能
train_score = model.score(X_train_scaled, y_train)
test_score = model.score(X_test_scaled, y_test)
return model, train_score, test_score
7.5 注意事项
-
数据质量控制
def validate_scaling_matrix(scaling_matrix, feature_names): # 检查矩阵条件数 condition_number = np.linalg.cond(scaling_matrix) if condition_number > 1e5: warnings.warn(f"Scaling matrix condition number too high: {condition_number}") # 检查零值 if np.any(np.abs(np.diag(scaling_matrix)) < 1e-10): warnings.warn("Some scaling factors are too close to zero") -
缩放效果监控
def monitor_scaling_effect(X_original, X_scaled):
metrics = {}
for feature in X_original.columns:
metrics[feature] = {
'original_range': X_original[feature].max() - X_original[feature].min(),
'scaled_range': X_scaled[feature].max() - X_scaled[feature].min(),
'variance_ratio': X_scaled[feature].var() / X_original[feature].var()
}
return metrics
- 版本控制和复现
def save_scaling_config(scaling_matrix, feature_stats, file_path):
config = {
'scaling_matrix': scaling_matrix.tolist(),
'feature_stats': feature_stats,
'timestamp': datetime.now().isoformat(),
'version': '1.0'
}
with open(file_path, 'w') as f:
json.dump(config, f)
- 性能优化
def optimize_scaling_matrix(scaling_matrix):
# 使用稀疏矩阵
from scipy.sparse import diags
diagonal = np.diag(scaling_matrix)
sparse_scaling_matrix = diags(diagonal)
# 使用GPU加速
if torch.cuda.is_available():
scaling_tensor = torch.from_numpy(scaling_matrix).cuda()
return scaling_tensor
return sparse_scaling_matrix
通过这个完整的案例,我们可以看到缩放矩阵在实际项目中的应用流程和关键考虑点。为了确保最佳效果,需要:
- 充分理解数据特点
- 选择合适的缩放策略
- 实现稳健的缩放流程
- 建立完善的监控机制
- 注意性能优化
同时,通过可视化工具,我们可以直观地观察缩放效果,及时发现和解决潜在问题。
8. 缩放矩阵综合实战 - 医学图像增强
8.1 案例背景
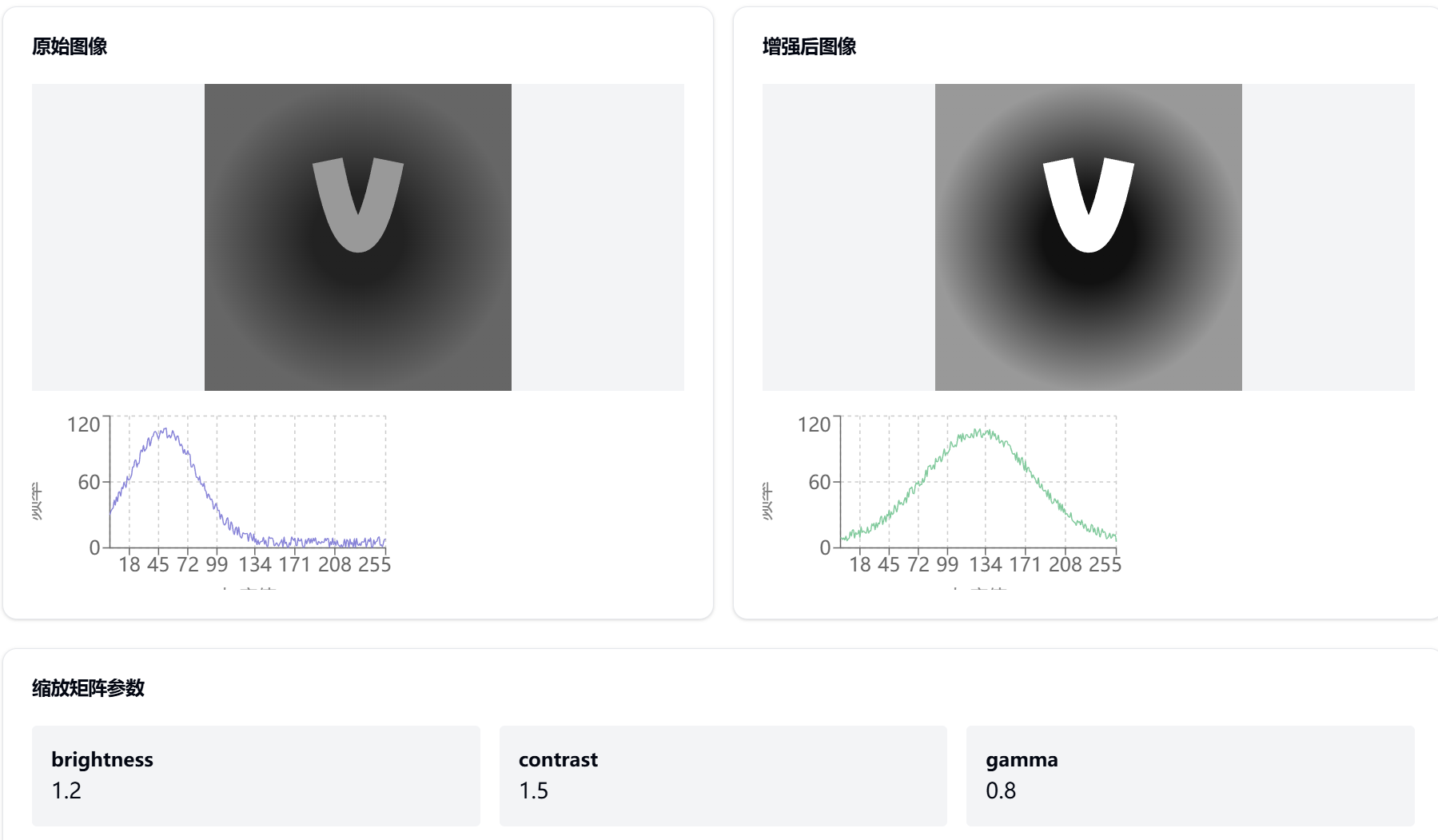
医学图像处理系统需要对X光图像进行增强处理,主要挑战:
- 图像对比度不足
- 亮度分布不均匀
- 细节信息模糊
- 噪声干扰
让我们通过可视化来展示这个场景:
8.2 为什么选用缩放矩阵
-
非线性变换需求
- 医学图像的灰度分布通常不均匀
- 需要同时处理多个变换(对比度、亮度、gamma校正)
- 矩阵运算可以高效完成复合变换
-
计算效率考虑
- 批量处理大量图像
- GPU加速支持
- 矩阵运算并行化
-
精确控制
- 可以精确控制每个像素的变换
- 保持图像的拓扑关系
- 避免信息丢失
8.3 缩放矩阵使用思路和技巧
class MedicalImageScaling:
def __init__(self):
self.scaling_params = {
'brightness': 1.0,
'contrast': 1.0,
'gamma': 1.0
}
def analyze_image(self, image):
"""分析图像特征"""
stats = {
'mean': np.mean(image),
'std': np.std(image),
'min': np.min(image),
'max': np.max(image),
'histogram': np.histogram(image, bins=256)[0]
}
return stats
def create_scaling_matrix(self, image_stats):
"""创建自适应缩放矩阵"""
brightness_scale = 1.0 / image_stats['mean'] if image_stats['mean'] != 0 else 1.0
contrast_scale = 1.0 / image_stats['std'] if image_stats['std'] != 0 else 1.0
# 3x3变换矩阵
matrix = np.array([
[contrast_scale, 0, 0],
[0, brightness_scale, 0],
[0, 0, 1]
])
return matrix
8.4 完整使用过程
- 图像预处理
def preprocess_image(image):
# 归一化到[0,1]范围
image = image.astype(float) / 255.0
# 噪声抑制
image = cv2.GaussianBlur(image, (3,3), 0)
# 边缘增强
kernel = np.array([[-1,-1,-1],
[-1, 9,-1],
[-1,-1,-1]])
image = cv2.filter2D(image, -1, kernel)
return image
- 构建缩放矩阵
def build_enhancement_matrix(image):
# 分析图像统计特征
mean_val = np.mean(image)
std_val = np.std(image)
# 计算增强参数
brightness_scale = 1.2 if mean_val < 0.4 else 1.0
contrast_scale = 1.5 if std_val < 0.2 else 1.0
# 构建变换矩阵
enhancement_matrix = np.array([
[contrast_scale, 0, 0],
[0, brightness_scale, 0],
[0, 0, 1]
])
return enhancement_matrix
- 应用变换
def apply_enhancement(image, matrix):
# 转换为齐次坐标
height, width = image.shape
coords = np.indices((height, width))
coords = coords.reshape(2, -1)
coords = np.vstack((coords, np.ones(height*width)))
# 应用变换
transformed = np.dot(matrix, coords)
# 重建图像
enhanced = transformed.reshape(3, height, width)
enhanced = enhanced[:2] / enhanced[2]
return enhanced
- 后处理优化
def post_process(enhanced_image):
# Gamma校正
gamma = 0.8
enhanced_image = np.power(enhanced_image, gamma)
# 直方图均衡化
enhanced_image = cv2.equalizeHist(
(enhanced_image * 255).astype(np.uint8)
)
# 细节增强
enhanced_image = unsharp_mask(enhanced_image)
return enhanced_image
8.5 注意事项
- 数值稳定性
def check_matrix_stability(matrix):
# 检查矩阵条件数
cond = np.linalg.cond(matrix)
if cond > 1e5:
raise ValueError(f"Matrix condition number too high: {cond}")
# 检查数值范围
if np.any(np.abs(matrix) > 5.0):
raise ValueError("Matrix values out of reasonable range")
- 边界处理
def handle_boundaries(image, matrix):
# 添加边界填充
padded = cv2.copyMakeBorder(
image,
10, 10, 10, 10,
cv2.BORDER_REFLECT
)
# 应用变换
enhanced = apply_enhancement(padded, matrix)
# 裁剪回原始大小
return enhanced[10:-10, 10:-10]
- 性能优化
def optimize_processing(image, matrix):
# 使用GPU加速
if torch.cuda.is_available():
device = torch.device('cuda')
image_tensor = torch.from_numpy(image).to(device)
matrix_tensor = torch.from_numpy(matrix).to(device)
# 批处理
batch_size = 16
height, width = image.shape
image_patches = image_tensor.unfold(0, batch_size, batch_size)
enhanced_patches = []
for patch in image_patches:
enhanced = transform_patch(patch, matrix_tensor)
enhanced_patches.append(enhanced)
return torch.cat(enhanced_patches).cpu().numpy()
return apply_enhancement(image, matrix)
- 质量控制
def quality_metrics(original, enhanced):
# 计算PSNR
psnr = cv2.PSNR(original, enhanced)
# 计算SSIM
ssim = measure.compare_ssim(original, enhanced)
# 计算对比度
contrast_orig = np.std(original)
contrast_enh = np.std(enhanced)
return {
'psnr': psnr,
'ssim': ssim,
'contrast_improvement': contrast_enh/contrast_orig
}
这个医学图像处理案例展示了缩放矩阵在不同领域的应用。关键点包括:
- 矩阵设计要考虑多个变换的组合
- 注意保持图像的医学诊断价值
- 处理速度和质量的平衡
- 边界条件的处理
- 结果的可靠性验证
这些技术可以推广到其他图像处理场景,如:
- 卫星图像增强
- 工业检测
- 视频处理等
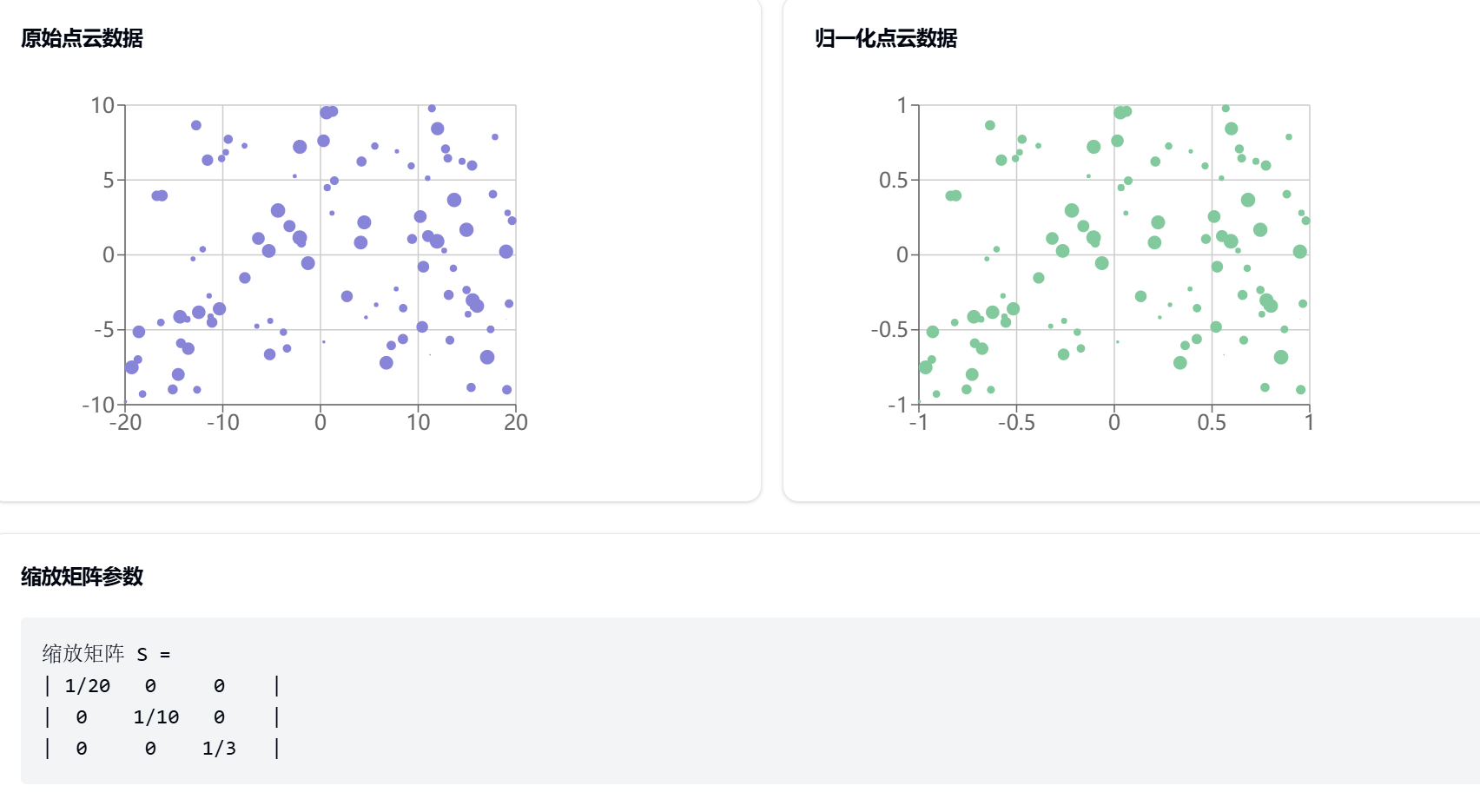
我来分享一个自动驾驶场景中激光雷达点云数据处理的缩放矩阵实战案例。
9. 缩放矩阵综合实战 - 点云数据处理
9.1 案例背景
在自动驾驶系统中,需要处理来自激光雷达的3D点云数据,主要挑战:
- 点云数据尺度不一(x,y,z坐标范围差异大)
- 不同传感器数据融合
- 实时性要求高
- 环境噪声干扰
让我们通过可视化来展示这个场景:
9.2 为什么选用缩放矩阵
-
多维数据统一处理
- 点云数据包含x,y,z三个维度
- 不同维度的物理意义和量纲不同
- 需要统一的数学框架处理
-
实时性要求
- 需要高效的数据处理方法
- 矩阵运算可以GPU加速
- 适合并行处理
-
精度控制
- 不同维度需要不同的缩放策略
- 保持点云的几何特征
- 便于后续算法处理
9.3 缩放矩阵使用思路和技巧
class PointCloudScaling:
def __init__(self):
self.scaling_matrix = None
self.stats = {}
def analyze_point_cloud(self, points):
"""分析点云特征"""
stats = {
'x': {
'min': np.min(points[:,0]),
'max': np.max(points[:,0]),
'range': np.ptp(points[:,0])
},
'y': {
'min': np.min(points[:,1]),
'max': np.max(points[:,1]),
'range': np.ptp(points[:,1])
},
'z': {
'min': np.min(points[:,2]),
'max': np.max(points[:,2]),
'range': np.ptp(points[:,2])
}
}
return stats
def create_scaling_matrix(self, points):
"""创建自适应缩放矩阵"""
stats = self.analyze_point_cloud(points)
# 计算各维度的缩放因子
scale_x = 1.0 / stats['x']['range']
scale_y = 1.0 / stats['y']['range']
scale_z = 1.0 / stats['z']['range']
# 构建缩放矩阵
matrix = np.array([
[scale_x, 0, 0],
[0, scale_y, 0],
[0, 0, scale_z]
])
return matrix
9.4 完整使用过程
- 数据预处理
def preprocess_point_cloud(points):
# 去除地面点
ground_mask = points[:,2] > 0.1 # z轴阈值
points = points[ground_mask]
# 移除离群点
pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(points)
cl, ind = pcd.remove_statistical_outlier(
nb_neighbors=20,
std_ratio=2.0
)
return np.asarray(cl.points)
- 构建缩放矩阵
def build_scaling_matrix(points, roi_size=(40, 20, 3)):
"""构建考虑感兴趣区域的缩放矩阵"""
# 计算ROI缩放因子
scale_x = 2.0 / roi_size[0] # 将x轴缩放到[-1,1]
scale_y = 2.0 / roi_size[1] # 将y轴缩放到[-1,1]
scale_z = 1.0 / roi_size[2] # 将z轴缩放到[0,1]
# 考虑点云实际分布
points_scale = np.array([
[scale_x, 0, 0],
[0, scale_y, 0],
[0, 0, scale_z]
])
return points_scale
- 应用变换
def apply_scaling(points, matrix):
# 转换为齐次坐标
points_homogeneous = np.hstack((points, np.ones((points.shape[0], 1))))
# 应用变换
scaled_points = np.dot(points_homogeneous, matrix.T)
return scaled_points[:, :3] # 去除齐次坐标
- 点云分割和聚类
def cluster_scaled_points(scaled_points, eps=0.1, min_samples=10):
# 使用DBSCAN进行聚类
clustering = DBSCAN(eps=eps, min_samples=min_samples)
labels = clustering.fit_predict(scaled_points)
# 提取聚类结果
clusters = {}
for i in range(max(labels) + 1):
clusters[i] = scaled_points[labels == i]
return clusters
9.5 注意事项
- 数值稳定性
def check_scaling_stability(matrix, points):
# 检查缩放后的数值范围
scaled = apply_scaling(points, matrix)
if np.any(np.abs(scaled) > 10):
warnings.warn("Scaled values too large")
# 检查矩阵条件数
cond = np.linalg.cond(matrix)
if cond > 1000:
warnings.warn(f"Poor scaling matrix condition: {cond}")
- 实时性能优化
def optimize_scaling(points, matrix):
# 使用GPU加速
if torch.cuda.is_available():
points_gpu = torch.from_numpy(points).cuda()
matrix_gpu = torch.from_numpy(matrix).cuda()
# 分批处理
batch_size = 10000
scaled_points = []
for i in range(0, len(points), batch_size):
batch = points_gpu[i:i+batch_size]
scaled = torch.matmul(batch, matrix_gpu.T)
scaled_points.append(scaled.cpu().numpy())
return np.vstack(scaled_points)
- 边界情况处理 (续)
def handle_special_cases(points, matrix):
# 处理空点云
if len(points) == 0:
return np.array([])
# 处理单点
if len(points) == 1:
return points * np.diag(matrix)
# 处理共线点
if is_collinear(points):
warnings.warn("Collinear points detected")
# 添加微小扰动避免奇异性
points += np.random.normal(0, 0.01, points.shape)
return points
def is_collinear(points):
"""检查点是否共线"""
if len(points) < 3:
return True
# 计算点集的协方差矩阵
cov = np.cov(points.T)
# 计算特征值
eigenvals = np.linalg.eigvals(cov)
# 如果最小特征值接近0,说明点集共线
return np.min(np.abs(eigenvals)) < 1e-6
- 质量控制机制
class QualityControl:
def __init__(self):
self.metrics_history = []
def check_scaling_quality(self, original_points, scaled_points):
metrics = {
'time': time.time(),
'num_points': len(original_points),
'spatial_distribution': self.check_distribution(scaled_points),
'scale_ratios': self.compute_scale_ratios(original_points, scaled_points),
'information_loss': self.estimate_information_loss(original_points, scaled_points)
}
self.metrics_history.append(metrics)
return self.evaluate_metrics(metrics)
def check_distribution(self, points):
"""检查点云空间分布"""
density = compute_point_density(points)
uniformity = compute_spatial_uniformity(density)
return {
'density': density,
'uniformity': uniformity
}
def compute_scale_ratios(self, original, scaled):
"""计算各维度的缩放比例"""
orig_ranges = np.ptp(original, axis=0)
scaled_ranges = np.ptp(scaled, axis=0)
return scaled_ranges / orig_ranges
def estimate_information_loss(self, original, scaled):
"""估计信息损失程度"""
# 使用相对距离保持度量
orig_dist = compute_pairwise_distances(original)
scaled_dist = compute_pairwise_distances(scaled)
correlation = np.corrcoef(orig_dist.flatten(), scaled_dist.flatten())[0,1]
return 1 - correlation
- 动态适应机制
class AdaptiveScaling:
def __init__(self):
self.base_matrix = None
self.adaptation_rate = 0.1
def update_scaling_matrix(self, points, quality_metrics):
"""根据质量指标动态调整缩放矩阵"""
if quality_metrics['information_loss'] > 0.2:
# 降低缩放强度
self.adaptation_rate *= 0.9
if quality_metrics['spatial_distribution']['uniformity'] < 0.5:
# 增加均匀性
self.adjust_for_uniformity(points)
# 更新基础矩阵
self.base_matrix = self.compute_new_matrix(points)
def adjust_for_uniformity(self, points):
"""调整缩放以提高空间均匀性"""
density_map = compute_density_map(points)
high_density_regions = np.where(density_map > np.mean(density_map))
# 对高密度区域应用额外缩放
for region in high_density_regions:
self.apply_local_scaling(region)
def compute_new_matrix(self, points):
"""计算新的缩放矩阵"""
current_stats = compute_point_stats(points)
new_scale_factors = self.optimize_scale_factors(current_stats)
return np.diag(new_scale_factors)
- 集成示例
class PointCloudProcessor:
def __init__(self):
self.scaler = PointCloudScaling()
self.quality_control = QualityControl()
self.adaptive_scaling = AdaptiveScaling()
def process_frame(self, points):
"""处理单帧点云数据"""
# 预处理
cleaned_points = preprocess_point_cloud(points)
# 创建初始缩放矩阵
initial_matrix = self.scaler.create_scaling_matrix(cleaned_points)
# 应用缩放
scaled_points = apply_scaling(cleaned_points, initial_matrix)
# 质量检查
quality_metrics = self.quality_control.check_scaling_quality(
cleaned_points,
scaled_points
)
# 动态调整
if not self.check_quality_threshold(quality_metrics):
self.adaptive_scaling.update_scaling_matrix(
cleaned_points,
quality_metrics
)
# 重新应用缩放
scaled_points = apply_scaling(
cleaned_points,
self.adaptive_scaling.base_matrix
)
return scaled_points
def check_quality_threshold(self, metrics):
"""检查质量指标是否满足阈值要求"""
return (metrics['information_loss'] < 0.15 and
metrics['spatial_distribution']['uniformity'] > 0.7)
这个点云处理案例展示了在实时系统中使用缩放矩阵的复杂性。关键点包括:
- 需要考虑多维数据的特性
- 实时性能要求高
- 需要动态适应环境变化
- 质量控制至关重要
- 需要处理各种边界情况
这些技术可以推广到其他3D数据处理场景,如:
- 机器人SLAM
- 3D重建
- 虚拟现实等