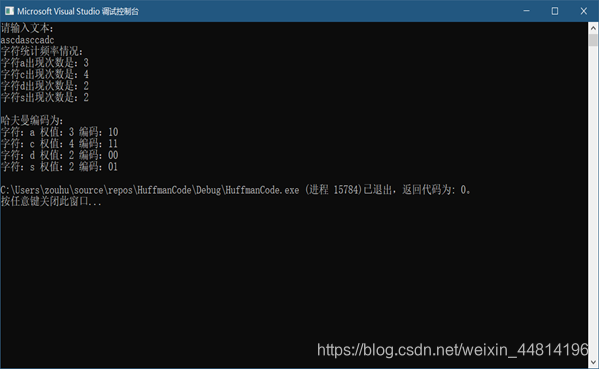
一、问题描述

给定一段文本，构造一棵哈夫曼树，给出文本中每个字符或词的编码。

二、实现思路

在该程序中，首先通过Frequency（）函数来分析输入文本中的字符数量以及其出现的次数，并将其次数作为权值。将文本信息存放到数组str中，数组的下标对应英文字母在英文字母表中的顺序，数组元素的值对应字母出现的次数。每当出现英文字母，就将其值加1.当扫描完文本后，将数组元素值不为0的数组元素转换为哈弗曼树的结点。
当生成哈弗曼树的结点后，调用函数CreateHT（），构造哈夫曼树。紧接着，调用CreateHCode（），根据哈夫曼树求对应的哈夫曼编码。最后，通过DisplayHCode（）来输出哈夫曼编码的序列。

三、解题代码

#include<iostream>

using namespace std;

#define N 5		//编码长度

/*哈夫曼树中的结点类型*/
typedef struct
{
	char data;		//结点值
	double weight;	//权重
	int parent;		//双亲结点
	int lchild;		//左孩子结点
	int rchild;		//右孩子结点
}HTNode;

/*存放每个结点的哈夫曼编码的类型*/
typedef struct
{
	char cd[N];		//存放当前结点的哈夫曼码
	int start;		//表示cd[strat..n0]部分是哈夫曼码
}HCode;

/*构造哈夫曼树*/
void CreateHT(HTNode ht[], int n0) //ht[]数组存放具有n0个叶子结点的哈夫曼树
{
	int i, k, lnode, rnode;			//min1,lnode分别是纪录权值最小的结点的大小和下标
	double min1,min2;				//min2,rnode分别是纪录权值第二小的结点的大小和下标
	for (i = 0; i < 2 * n0 - 1; i++)//所有结点的相关域置为-1
	{
		ht[i].parent = ht[i].lchild = ht[i].rchild = -1;
	}
	for (i = n0; i <= 2 * n0 - 2; i++)		//构造哈夫曼树的n0-1个分支结点
	{
		min1 = min2 = 32767;				//保证其权值最大
		lnode = rnode = -1;
		for (k = 0; k <= i - 1; k++)			//在ht[0...i-1]中找权值最小的两个结点
		{
			if (ht[k].parent == -1)				//只在尚未构造二叉树的结点中查找
			{
				if (ht[k].weight < min1)			//如果有比当前min1小的结点
				{									//那么min2就会继承之前的那个min1的值(包括结点)
					min2 = min1; rnode = lnode;		//并更新min1和lnode
					min1 = ht[k].weight; lnode = k;
				}
				else if (ht[k].weight < min2)
				{
					min2 = ht[k].weight;
					rnode = k;
				}
			}
		}
		ht[i].weight = ht[lnode].weight + ht[rnode].weight;		//ht[i]作为双亲结点
		ht[i].lchild = lnode; ht[i].rchild = rnode;
		ht[lnode].parent = i; ht[rnode].parent = i;	
	}
}

/*根据哈夫曼树求对应的哈夫曼编码*/
void CreateHCode(HTNode ht[], HCode hcd[], int n0)
{
	int i, f, c;							//c指向当前结点，f指向当前结点双亲结点
	HCode hc;
	for (i = 0; i < n0; i++)				//根据哈夫曼树求哈夫曼编码
	{
		hc.start = n0; c = i;
		f = ht[i].parent;
		while (f!=-1)						//循环直到无双亲结点。即到达根节点
		{
			if (ht[f].lchild==c)			//当前结点是双亲结点的左孩子
			{
				hc.cd[hc.start--] = '0';
			}
			else							//当前结点是双亲结点的右孩子
			{
				hc.cd[hc.start--] = '1';
			}
			c = f; f = ht[f].parent;		//再对双亲结点进行同样的操作
		}
		hc.start++;							//start指向哈夫曼编码最开始的字符
		hcd[i] = hc;
	}
}


/*输出哈夫曼编码的序列*/
void DisplayHCode(HTNode ht[], HCode hcd[], int n0)
{
	cout << "\n哈夫曼编码为：" << endl;
	for (int i = 0; i < n0; i++)
	{
		cout << "字符：" << ht[i].data<<" 权值："<<ht[i].weight << " 编码：";
		for (int j = hcd[i].start;j<=n0; j++)			//输出字符的编码
		{
			cout << hcd[i].cd[j];
		}
		cout << '\n';
	}
}

/*统计字符的出现字数*/
void Frequency(HTNode *ht,int *str,int &n0)
{
	char s[50];
	cout << "请输入文本：" << endl;
	cin >> s;
	int i = 0;
	char c;
	int index=0;
	while (*(s+i)!='\0')				//统计频率并将其次数存放到数组str
	{
		c = *(s + i);
		if (c>='a'&&c<='z')
		{
			index = c - 'a';
			str[index] = str[index] + 1;
		}
		else if (c >= 'A'&&c <= 'Z')
		{
			index = c - 'A';
			str[index] = str[index] + 1;
		}
		i++;
	}
	
	cout << "字符统计频率情况：" << endl;
	for (int i = 0; i < 26; i++)
	{
		if (str[i] != 0)
		{
			n0++;
			cout << "字符" << (char)(i + 'a') << "出现次数是：" << str[i] << endl;
		}
	}

	int j = 0;								//将数组str转换为哈夫曼树的结点
	for (int i = 0; i < 26; i++)
	{
		if (str[i] != 0)
		{
			ht[j].data = (char)(i + 'a');
			ht[j].weight = str[i];
			j++;
		}
		else
		{
			continue;
		}
	}
}

int main()
{
	int str[26] = { 0 };
	int n0=0;
	HTNode ht[200];
	HCode hcd[26];
	Frequency(ht,str,n0);
	CreateHT(ht, n0);
	CreateHCode(ht, hcd, n0);
	DisplayHCode(ht, hcd, n0);
}

四、运行结果