1.题目描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
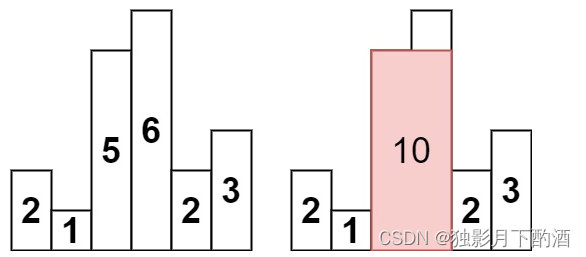
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
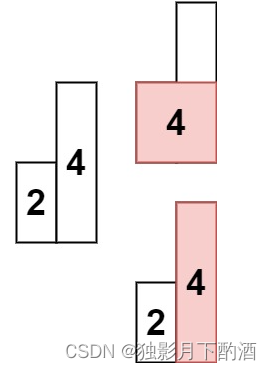
输入: heights = [2,4]
输出: 4
提示:
- 1 <= nums1.length <= nums2.length <= 1000
- 0 <= nums1[i], nums2[i] <= 104
- nums1和nums2中所有整数 互不相同
- nums1 中的所有整数同样出现在 nums2 中
2.思路分析
求在该柱状图中,能够勾勒出来的矩形的最大面积。
2.1 动态规划
对于下标i而言,能勾勒出的最大面积是什么?
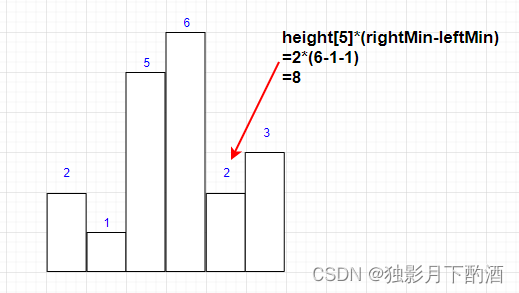
以i为中心, 向左寻找第一个小于height[i]的位置leftMin, 向右寻找第一个小于height[i]的rightMin, 即最大面积=height[i] *(rightMin - leftMin - 1)
举个栗子:heights = [2,1,5,6,2,3],对于下标5(元素2)而言:
-
定义两个长度为n的数组leftMin和rightMin
- leftMin[i]:左边第一个小于下标i的柱子的下标
- rightMin[i]:右边第一个小于下标i柱子的下标
-
leftMin[0] = -1 rightMin[n-1] = n
-
正向遍历数组 height 得到数组 leftMin 的每个索引值(第一小于当前柱子高度的索引值),反向遍历数组 height 得到数组rightMin (第一小于当前柱子高度的索引值)
-
遍历结束之后,下标i处能勾勒出的最大面积:= heights[i] * (righMin[i] -leftMin[i] - 1)
2.2 单调栈
Leetcode 42.接雨水是找每个柱子左右两边第一个大于该柱子高度的柱子,而本题是找每个柱子左右两边第一个小于该柱子的柱子。
Q1:单调栈内的元素顺序?
维护一个单调栈, 单调栈存储的元素的下标, 栈顶->栈底:递增(小->大)
一旦发现添加的柱子高度小于栈顶元素,此时就会出现凸起, 栈顶元素就是凸起顶部的柱子, 栈顶的第二个元素就是凸起左边的柱子, 当前元素就是凸起右边的柱子。
Q2:遇到相同柱子如何处理?
遇到相同的元素,更新栈内下标,就是将栈里元素(旧下标)弹出,将新元素(新下标)加入栈中。
单调栈的处理逻辑:
-
情况1:当前遍历元素高度 > 栈顶元素的高度, 当前元素入栈(保持 大>小 单调的性质 )
-
情况2: 当前遍历元素高度 == 栈顶元素高度, 更新栈顶元素(遇到相同柱子,使用右边柱子计算高度)
-
情况3: 当前遍历元素高度 < 栈顶元素, 此时出现凸起, 弹出栈顶元素(凸起顶部柱子, 记为mid), 此时
栈顶元素(stack.top())(凸起左边的柱子, height[st.top()]), 当前元素记为凸起右边的柱子(height[i])
- 矩形高度: w = heights[i]
- 矩形宽度: l = i - stack.top() -1
- 矩形的面积:l * w
3.代码实现
3.1 动态规划
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
# 动态规划
if not heights:
return 0
n = len(heights)
# 两个数组存储的下标
leftMin = [0] * n
rightMin = [0] * n
result = 0
leftMin[0], rightMin[n-1] = -1, n
# 正向遍历数组
for i in range(1, n):
temp = i - 1
while temp >= 0 and heights[temp] >= heights[i]:
# 寻找次级柱子
temp = leftMin[temp]
# 寻找到左侧第一个小于当前柱子高度的下标
leftMin[i] = temp
# 反向遍历数组
for i in range(n - 2, -1, -1):
temp = i + 1
while temp < n and heights[temp] >= heights[i]:
# 寻找次级柱子
temp = rightMin[temp]
rightMin[i] = temp
for i in range(n):
area = heights[i] * (rightMin[i] - leftMin[i] - 1)
result = max(area, result)
return result
复杂度分析
- 时间复杂度:O(n)。
- 空间复杂度:O(n)。
3.2 单调栈
# 方式1
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
heights.insert(0, 0)
heights.append(0)
stack = [0]
result = 0
for i in range(1, len(heights)):
# 情况一
if heights[i] > heights[stack[-1]]:
stack.append(i)
# 情况二
elif heights[i] == heights[stack[-1]]:
stack.pop()
stack.append(i)
# 情况三
else:
# 抛出所有较高的柱子
while stack and heights[i] < heights[stack[-1]]:
# 栈顶就是中间的柱子,主心骨
mid_index = stack[-1]
stack.pop()
if stack:
left_index = stack[-1]
right_index = i
width = right_index - left_index - 1
height = heights[mid_index]
result = max(result, width * height)
stack.append(i)
return result
# 方式2
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
heights.insert(0, 0)
heights.append(0)
stack = [0]
result = 0
for i in range(1, len(heights)):
while stack and heights[i] < heights[stack[-1]]:
mid_height = heights[stack[-1]]
stack.pop()
if stack:
# area = width * height
area = (i - stack[-1] - 1) * mid_height
result = max(area, result)
stack.append(i)
return result
# 方式3:
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
if not heights:
return 0
heights.insert(0, 0)
heights.append(0)
stack = []
result = 0
for i in range(len(heights)):
while stack and heights[i] <= heights[stack[-1]]:
height = heights[stack.pop()]
if stack:
w = i - stack[-1] - 1
result = max(result, height * w)
stack.append(i)
return result
复杂度分析
- 时间复杂度:O(n)。
- 空间复杂度:O(n)。