占主导地位的序列转导模型是基于复杂的递归(RNN)或卷积神经网络(CNN)的编码器-解码器(Encoder-Decoder)配置。性能最好的模型还通过注意机制将编码器和解码器连接起来。我们提出了一个新的简单的网络结构–Transformer,它只基于注意力机制,完全不需要递归(RNN)和卷积(CNN)。在两个机器翻译任务上的实验表明,这些模型在质量上更胜一筹,同时更容易并行化,所需的训练时间也大大减少。我们的模型在WMT 2014英德翻译任务中达到了28.4 BLEU,比现有的最佳结果(包括合集)提高了2 BLEU以上。在WMT 2014英法翻译任务中,我们的模型在8个GPU上训练了3.5天后,建立了新的单模型最先进的BLEU得分,即41.8分,只是文献中最佳模型的训练成本的一小部分。我们通过将其成功地应用于有大量和有限训练数据的英语选区解析,表明Transformer可以很好地推广到其他任务。
The dominant sequence transduction models are based on complex recurrent or convolutional neural networks in an encoder-decoder configuration. The best performing models also connect the encoder and decoder through an attention mechanism. We propose a new simple network architecture, the Transformer, based solely on attention mechanisms, dispensing with recurrence and convolutions entirely. Experiments on two machine translation tasks show these models to be superior in quality while being more parallelizable and requiring significantly less time to train. Our model achieves 28.4 BLEU on the WMT 2014 English-to-German translation task, improving over the existing best results, including ensembles by over 2 BLEU. On the WMT 2014 English-to-French translation task, our model establishes a new single-model state-of-the-art BLEU score of 41.8 after training for 3.5 days on eight GPUs, a small fraction of the training costs of the best models from the literature. We show that the Transformer generalizes well to other tasks by applying it successfully to English constituency parsing both with large and limited training data.
0. 引言
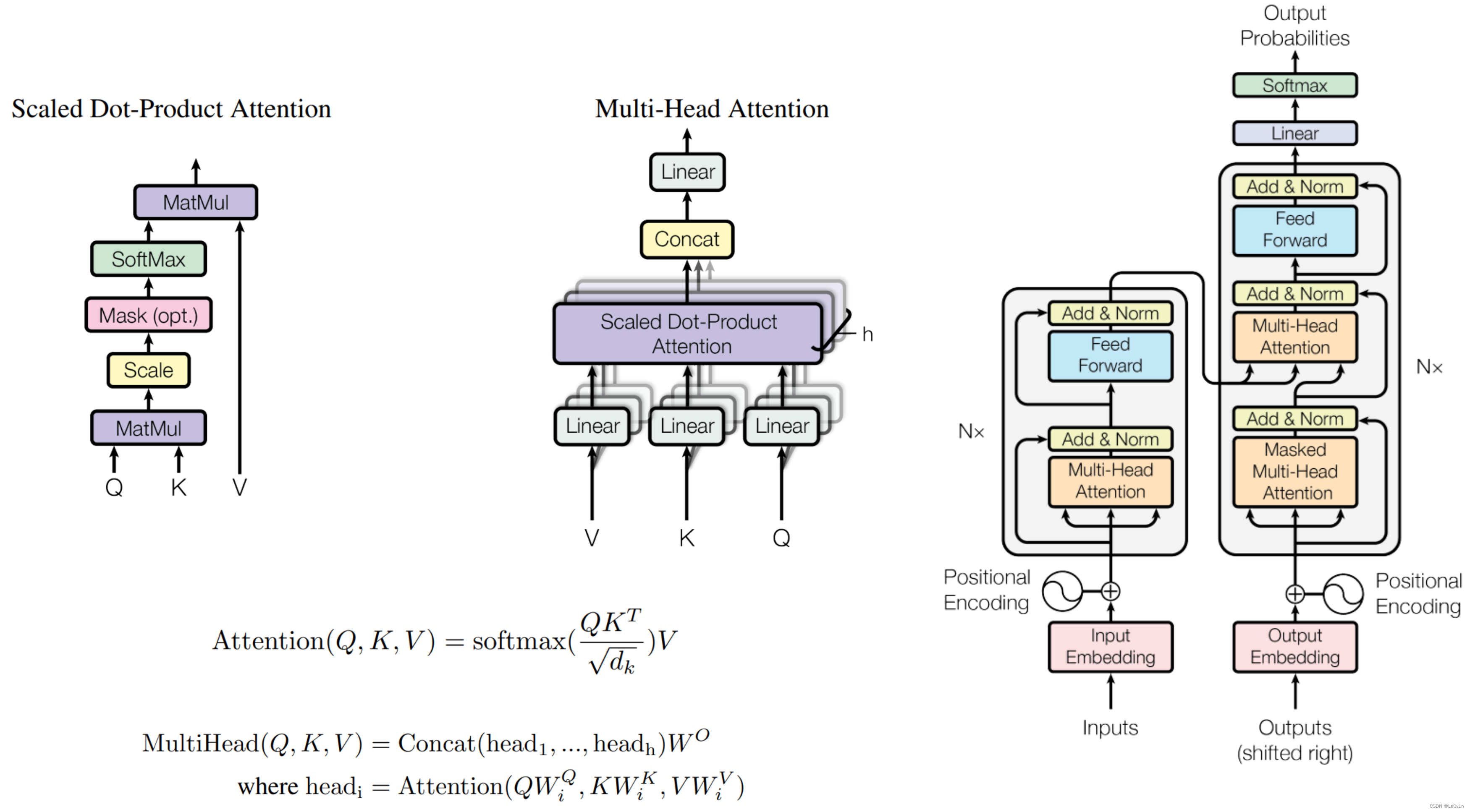
最近Transformer在CV领域很火,Transformer是2017年Google在Computation and Language上发表的,当时主要是针对自然语言处理领域提出的(之前的RNN模型①记忆长度有限且②无法并行化,只有计算完 t i t_i ti 时刻后的数据才能计算 t i + 1 t_{i+1} ti+1 时刻的数据,但Transformer都可以做到)。在这篇文章中作者提出了Self-Attention的概念,然后在此基础上提出Multi-Head Attention,所以本文对Self-Attention以及Multi-Head Attention的理论进行详细的讲解。
相比与RNN而言:
- 如果没有硬件的制约,Transformer在理论上的记忆长度是无限的
- Transfomrer是可以做并行化的
1. Self-Attention
下面这个图为了方便大家理解,假设输入的序列长度为
2
2
2,输入就两个节点
x
1
,
x
2
x_1, x_2
x1,x2,然后通过Input Embedding也就是图中的
f
(
x
)
f(x)
f(x) 将输入映射到更高的维度上,也就是图中的
a
1
,
a
2
a_1, a_2
a1,a2。紧接着将
a
1
,
a
2
a_1, a_2
a1,a2 分别通过三个变换矩阵
W
q
,
W
k
,
W
v
W_q, W_k, W_v
Wq,Wk,Wv(这三个参数是可训练的,是共享的)得到对应的
q
i
,
k
i
,
v
i
q^i, k^i, v^i
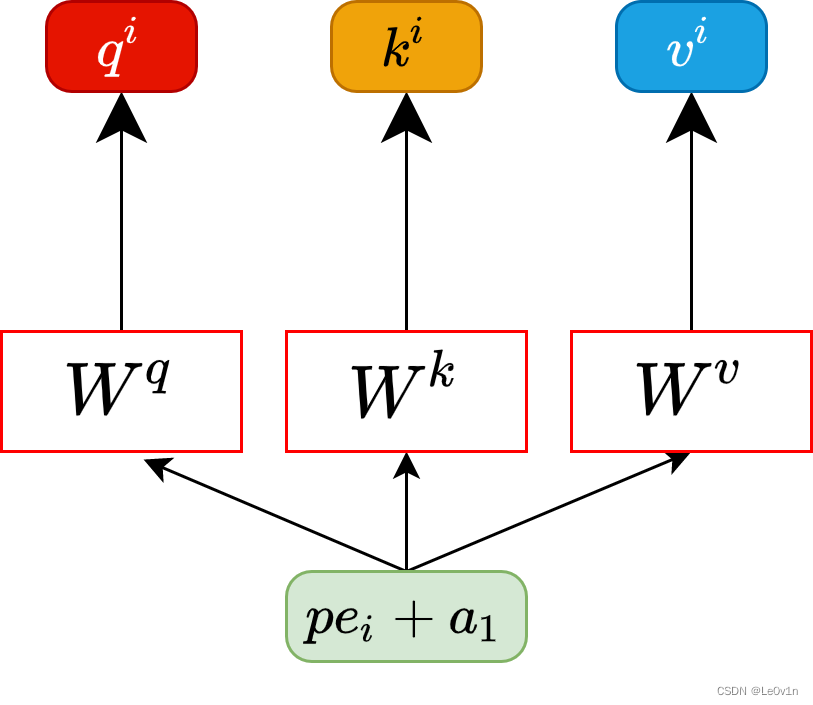
qi,ki,vi。
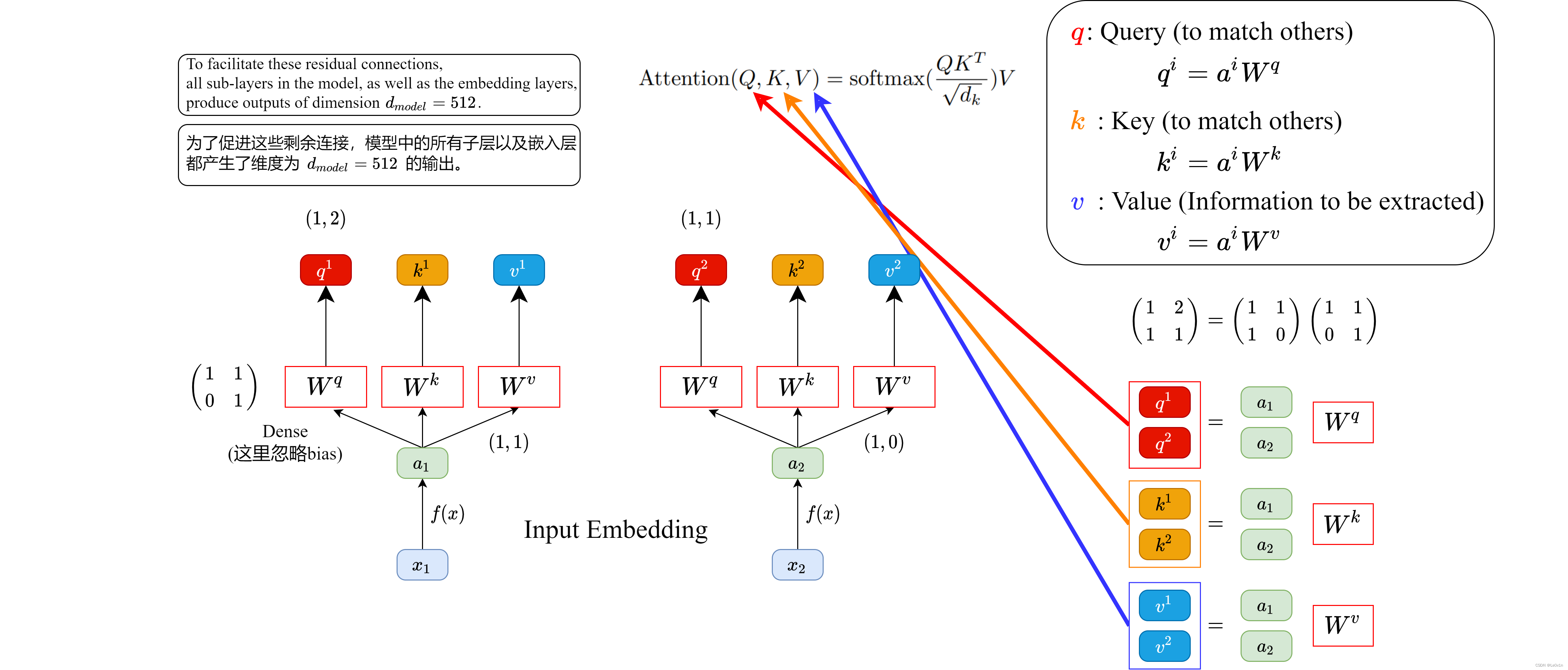
这里在源码中是直接使用全连接层
nn.Linear()实现的,这里为了方便理解,忽略偏执。
其中:
- q q q 代表 Q u e r y Query Query,后续会去和每一个 k k k 进行匹配
- k k k 代表 K e y Key Key,后续会被每个 q q q 匹配
- v v v 代表从 a a a 中提取得到的信息( v v v是通过学习得到的)
- 后续 q q q 和 k k k 匹配的过程可以理解成计算两者的相关性,相关性越大对应 v v v 的权重也就越大
- 将 q q q 全部放在一起就是我们Attention公式中的 Q Q Q
- 将 k k k 全部放在一起就是我们Attention公式中的 K K K
- 将 v v v 全部放在一起就是我们Attention公式中的 V V V
假设 a 1 = ( 1 , 1 ) , a 2 = ( 1 , 0 ) , W q = ( 1 , 1 0 , 1 ) a_1 = (1, 1), a_2 = (1, 0), W^q = \left(\begin{matrix} 1,1 \\ 0,1 \end{matrix}\right) a1=(1,1),a2=(1,0),Wq=(1,10,1),那么:
q 1 = ( 1 , 1 ) ( 1 , 1 0 , 1 ) = ( 1 , 2 ) q 2 = ( 1 , 0 ) ( 1 , 1 0 , 1 ) = ( 1 , 1 ) q^1 = (1, 1) \left(\begin{matrix} 1,1 \\ 0,1 \end{matrix}\right) = (1, 2) \\ q^2 = (1, 0) \left(\begin{matrix} 1,1 \\ 0,1 \end{matrix}\right) = (1, 1) q1=(1,1)(1,10,1)=(1,2)q2=(1,0)(1,10,1)=(1,1)
前面有说Transformer是可以并行化的,所以可以直接写成:
( q 1 q 2 ) = ( 1 , 1 1 , 0 ) ( 1 , 1 0 , 1 ) = ( 1 , 2 1 , 1 ) \left(\begin{matrix} q^1 \\ q^2 \end{matrix}\right) = \left(\begin{matrix} 1, 1 \\ 1, 0 \end{matrix}\right) \left(\begin{matrix} 1, 1 \\ 0,1 \end{matrix}\right) = \left(\begin{matrix} 1, 2 \\ 1, 1 \end{matrix}\right) (q1q2)=(1,11,0)(1,10,1)=(1,21,1)
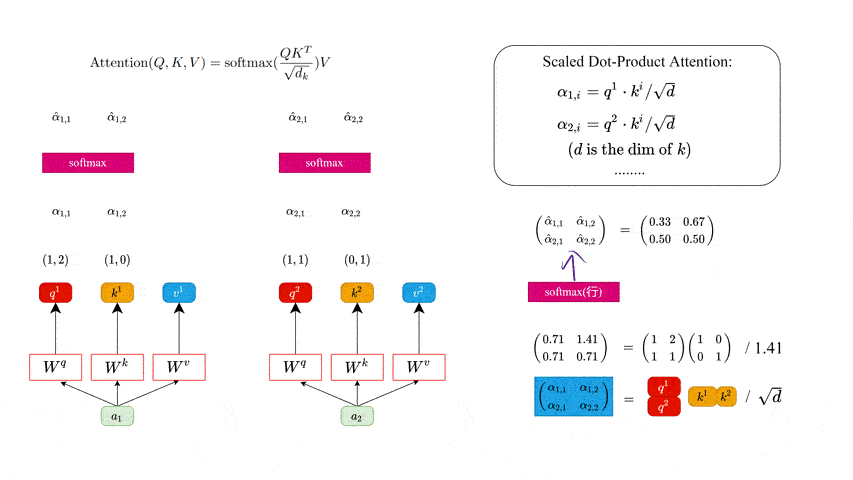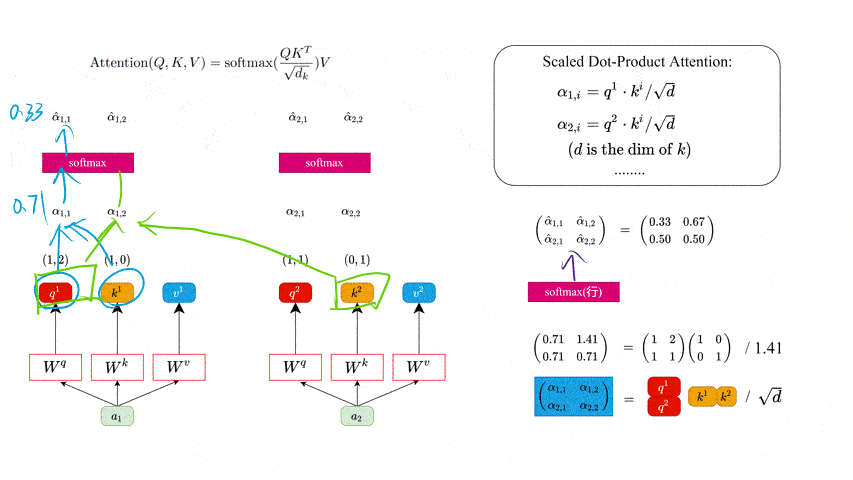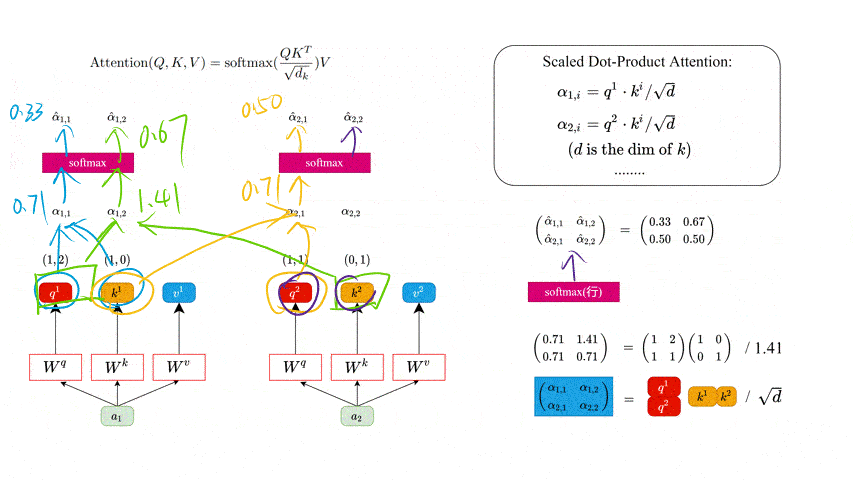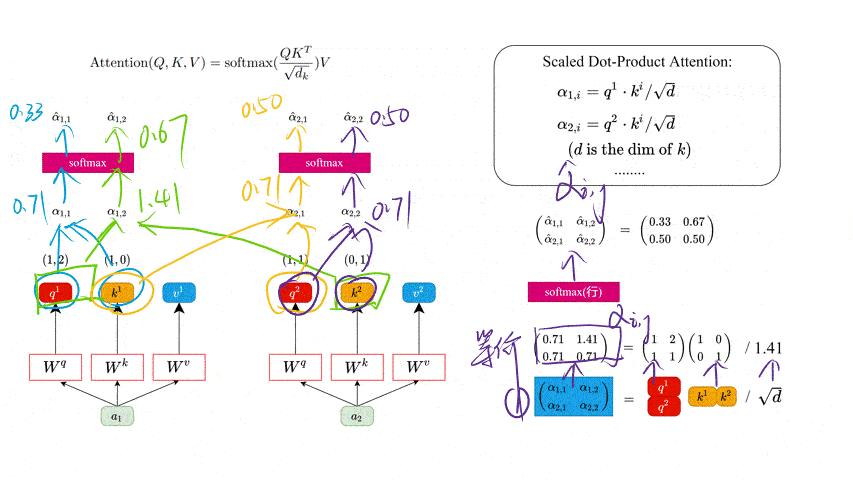
同理我们可以得到 ( k 1 k 2 ) \binom{k^1}{k^2} (k2k1) 和 ( v 1 v 2 ) \binom{v1}{v2} (v2v1),那么求得的 ( q 1 q 2 ) \binom{q^1}{q^2} (q2q1) 就是原论文中的 Q Q Q, ( k 1 k 2 ) \binom{k^1}{k^2} (k2k1) 就是 K K K, ( v 1 v 2 ) \binom{v1}{v2} (v2v1)就是 V V V。接着先拿 q 1 q^1 q1 和每个 k k k 进行match,点乘操作 ⋅ \cdot ⋅,接着除以 d \sqrt{d} d 得到对应的 α \alpha α,其中 d d d 代表向量 k i k^i ki 的长度,在本示例中等于 2 2 2,除以 d \sqrt{d} d 的原因在论文中的解释是“进行点乘 ⋅ \cdot ⋅后的数值很大,导致通过softmax后梯度变的很小”,所以通过除以 d \sqrt{d} d 来进行缩放。比如计算 α 1 , i \alpha_{1, i} α1,i:
α 1 , 1 = q 1 ⋅ k 1 d = 1 × 1 + 2 × 0 2 = 0.71 α 1 , 2 = q 1 ⋅ k 2 d = 1 × 0 + 2 × 1 2 = 1.41 \alpha_{1,1} = \frac{q^1 \cdot k^1}{\sqrt{d}} = \frac{1\times 1 + 2\times 0}{\sqrt{2}} = 0.71 \\ \alpha_{1,2} = \frac{q^1 \cdot k^2}{\sqrt{d}} = \frac{1\times 0 + 2\times 1}{\sqrt{2}} = 1.41 \\ α1,1=dq1⋅k1=21×1+2×0=0.71α1,2=dq1⋅k2=21×0+2×1=1.41
同理拿 q 2 q^2 q2 去匹配所有的 k k k 能得到 α 2 , i \alpha_{2, i} α2,i。
点乘 ⋅ \cdot ⋅ 的意思就是:两个向量对应位置元素进行相乘,最后在相加。点乘得到的是一个数而非向量。
统一写成矩阵乘法形式:
( α 1 , 1 α 1 , 2 α 2 , 1 α 2 , 2 ) = ( q 1 q 2 ) ( k 1 k 2 ) T d \left( \begin{matrix} \alpha_{1, 1} & \alpha_{1, 2}\\ \alpha_{2, 1} & \alpha_{2, 2}\\ \end{matrix} \right) = \frac{\binom{q^1}{q^2} \binom{k^1}{k^2}^T}{\sqrt{d}} (α1,1α2,1α1,2α2,2)=d(q2q1)(k2k1)T
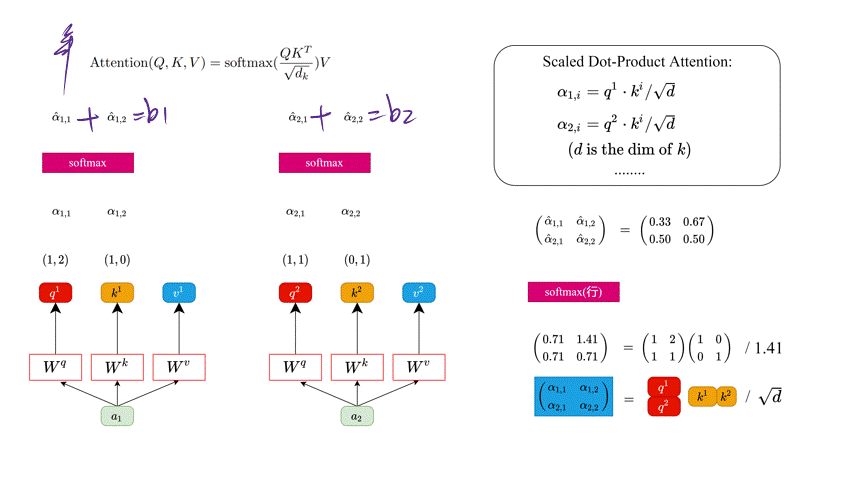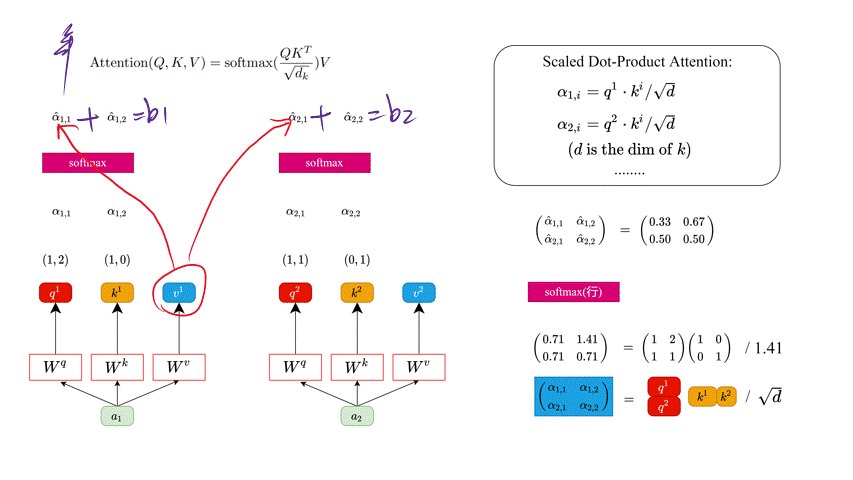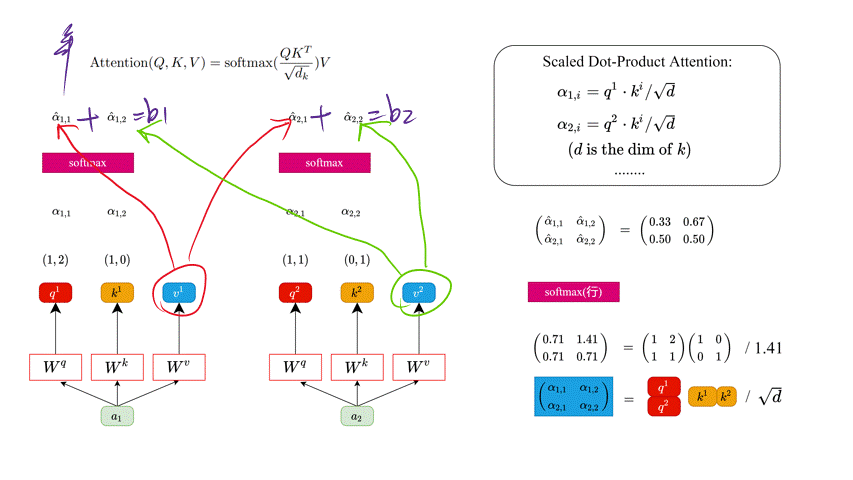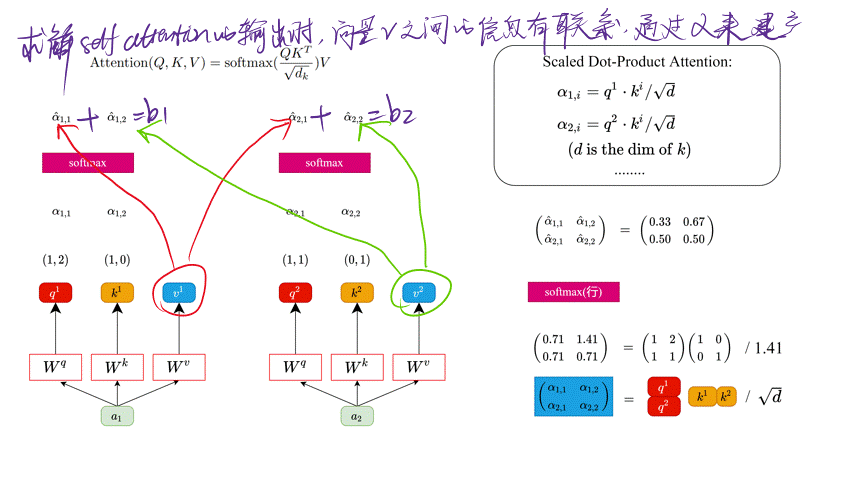
接着对每一行即 ( α 1 , 1 , α 1 , 2 ) (\alpha_{1, 1}, \alpha_{1, 2}) (α1,1,α1,2) 和 ( α 2 , 1 , α 2 , 2 ) (\alpha_{2, 1}, \alpha_{2, 2}) (α2,1,α2,2) 分别进行softmax处理得到 ( α ^ 1 , 1 , α ^ 1 , 2 ) (\hat\alpha_{1, 1}, \hat\alpha_{1, 2}) (α^1,1,α^1,2) 和 ( α ^ 2 , 1 , α ^ 2 , 2 ) (\hat\alpha_{2, 1}, \hat\alpha_{2, 2}) (α^2,1,α^2,2),这里的 α ^ \hat{\alpha} α^ 相当于计算得到针对每个 v v v 的权重。到这我们就完成了 A t t e n t i o n ( Q , K , V ) {\rm Attention}(Q, K, V) Attention(Q,K,V) 公式中 s o f t m a x ( Q K T d k ) {\rm softmax}(\frac{QK^T}{\sqrt{d_k}}) softmax(dkQKT) 部分。
此时求出来的 α ^ i , j \hat{\alpha}_{i, j} α^i,j 的值就是 计算得到针对每一个 v v v 的权重。这个权重越大,网络就会越关注某一个 v v v。
上面的计算过程如下图所示。
CSDN不允许上传大于5MB的图片😢 所以图片有点模糊
上面已经计算得到 α ^ \hat{\alpha} α^,即针对每个 v v v 的权重,接着对 v v v 进行加权得到最终结果:
b 1 = α ^ 1 , 1 × v 1 + α ^ 1 , 2 × v 2 = ( 0.33 , 0.67 ) b 2 = α ^ 2 , 1 × v 1 + α ^ 2 , 2 × v 2 = ( 0.50 , 0.50 ) b_1= \hat{\alpha}_{1, 1} \times v^1 + \hat{\alpha}_{1, 2} \times v^2 = (0.33, 0.67) \\ b_2= \hat{\alpha}_{2, 1} \times v^1 + \hat{\alpha}_{2, 2} \times v^2 = (0.50, 0.50) b1=α^1,1×v1+α^1,2×v2=(0.33,0.67)b2=α^2,1×v1+α^2,2×v2=(0.50,0.50)
统一写成矩阵乘法形式:
( b 1 b 2 ) = ( α ^ 1 , 1 α ^ 1 , 2 α ^ 2 , 1 α ^ 2 , 2 ) ( v 1 v 2 ) \binom{b_1}{b_2} = \binom{\hat{\alpha}_{1, 1} \ \ \hat{\alpha}_{1, 2}}{\hat{\alpha}_{2, 1} \ \ \hat{\alpha}_{2,2}} \binom{v^1}{v^2} (b2b1)=(α^2,1 α^2,2α^1,1 α^1,2)(v2v1)
上面的计算过程如下图所示:
通过上面对 b i b_i bi 的求解可以看到,在求解Self-Attention的输出时, v i v^i vi 之间是有联系的,通过 α ^ i , j \hat{\alpha}_{i,j} α^i,j 来建立不同 v i v_i vi 之间的联系(其实说白了是通过 不同的 q i , k i q^i, k^i qi,ki 匹配结果来建立不同 v i v^i vi 之间的联系)
到这里,Self-Attention的内容就讲完了。总结下来就是论文中的一个公式:
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V {\rm Attention}(Q, K, V) = {\rm softmax}(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dkQKT)V
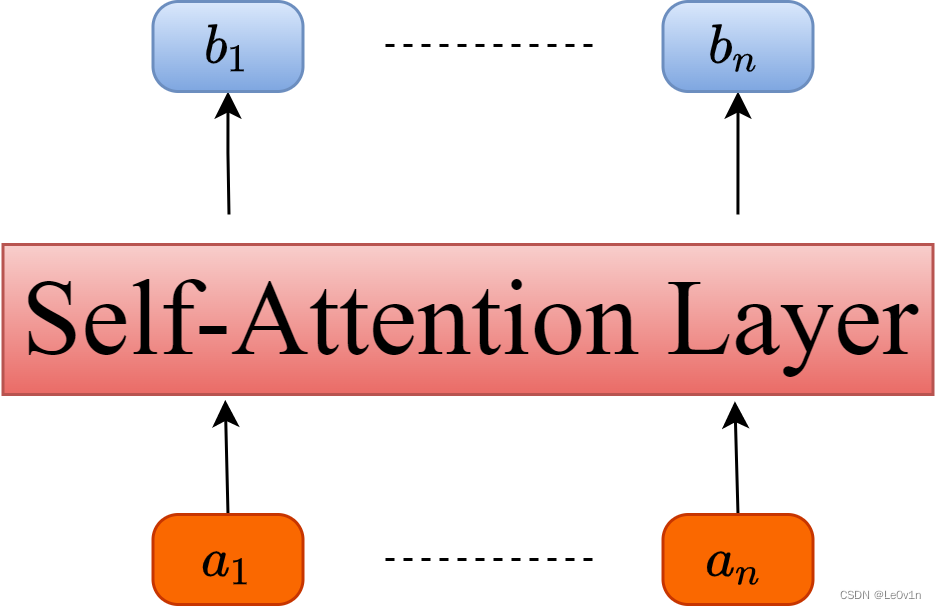
如果我们将Self-Attention抽象为一个模块的话,那么如下图所示。
输入向量 a i a_i ai,经过Self-Attention模块后输出向量 b i b_i bi。
2. Multi-Head Attention(Multi-Head Self-Attention, MSA)
刚刚已经聊完了Self-Attention模块,接下来再来看看Multi-Head Attention模块,实际使用中基本使用的还是Multi-Head Attention模块(MSA)。原论文中说使用多头注意力机制(MSA)能够联合来自不同head部分学习到的信息。
Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions.
多头注意允许模型在不同的位置上共同关注来自不同表征子空间的信息。
其实只要懂了Self-Attention模块Multi-Head Attention模块就非常简单了。
首先还是和Self-Attention模块一样将
a
i
a_i
ai 分别通过
W
q
,
W
k
,
W
v
W^q, W^k, W^v
Wq,Wk,Wv 得到对应的
q
i
,
k
i
,
v
i
q^i, k^i, v^i
qi,ki,vi,然后再根据使用的head的数目
h
h
h 进一步把得到的
q
i
,
k
i
,
v
i
q^i, k^i, v^i
qi,ki,vi 均分成
h
h
h 份。比如下图中假设
h
=
2
h=2
h=2,将
q
1
q^1
q1 拆分成
q
1
,
1
q^{1,1}
q1,1 和
q
1
,
2
q^{1,2}
q1,2,那么
q
1
,
1
q^{1,1}
q1,1 就属于head1,
q
1
,
2
q^{1,2}
q1,2 属于head2。
意思是说,拆分之后后面的数字表示该向量所属的head
通过上述方法就能得到每个
h
e
a
d
i
head_i
headi 对应的
Q
i
,
K
i
,
V
i
Q_i, K_i, V_i
Qi,Ki,Vi 参数,接下来针对每个
h
e
a
d
head
head 使用和Self-Attention中相同的方法即可得到对应的结果。
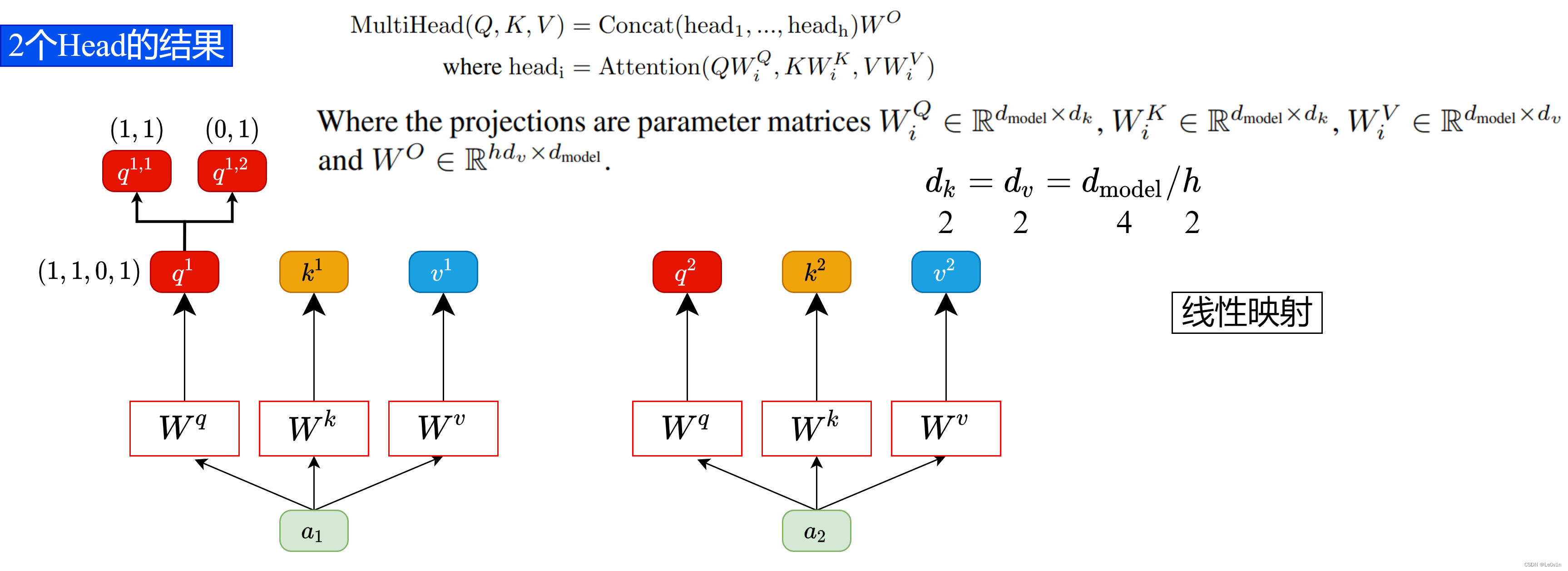
这里我们假设head=2。求得的 q 1 = ( 1 , 1 , 0 , 1 ) q^1=(1, 1, 0, 1) q1=(1,1,0,1),那么我们就拆成 h e a d = 2 head=2 head=2 份儿。在源码中,就是简单的将 q 1 q^1 q1 均分为 h e a d head head 份儿。
看到这里,如果读过原论文的人肯定有疑问,论文中不是写的通过 W i Q , W i K , W i V W^Q_i, W^K_i, W^V_i WiQ,WiK,WiV映射得到每个head的 Q i , K i , V i Q_i, K_i, V_i Qi,Ki,Vi 吗?
的确是这样的,在论文中,作者说通过一个线性映射得到的,如下面的公式:
h e a d i = A t t e n t i o n ( Q W i Q , K W i K , V W i V ) {\rm head_i} = {\rm Attention}(QW_i^Q, KW^K_i, VW_i^V) headi=Attention(QWiQ,KWiK,VWiV)
对于我们的 h e a d i head_i headi 而言,将 Q Q Q 乘上 W i Q W_i^Q WiQ 得到对应MSA输入的 Q Q Q, K , V K, V K,V 也是同理。
但在 github中的源码中就是简单的进行均分,其实也可以将
W
i
Q
,
W
i
K
,
W
i
V
W^Q_i, W^K_i, W^V_i
WiQ,WiK,WiV 设置成对应值来实现均分。为了方便理解,我们就可以简单粗暴地理解为MSA的
Q
,
K
,
V
Q, K, V
Q,K,V 就是根据
h
e
a
d
head
head 的个数均分得到。
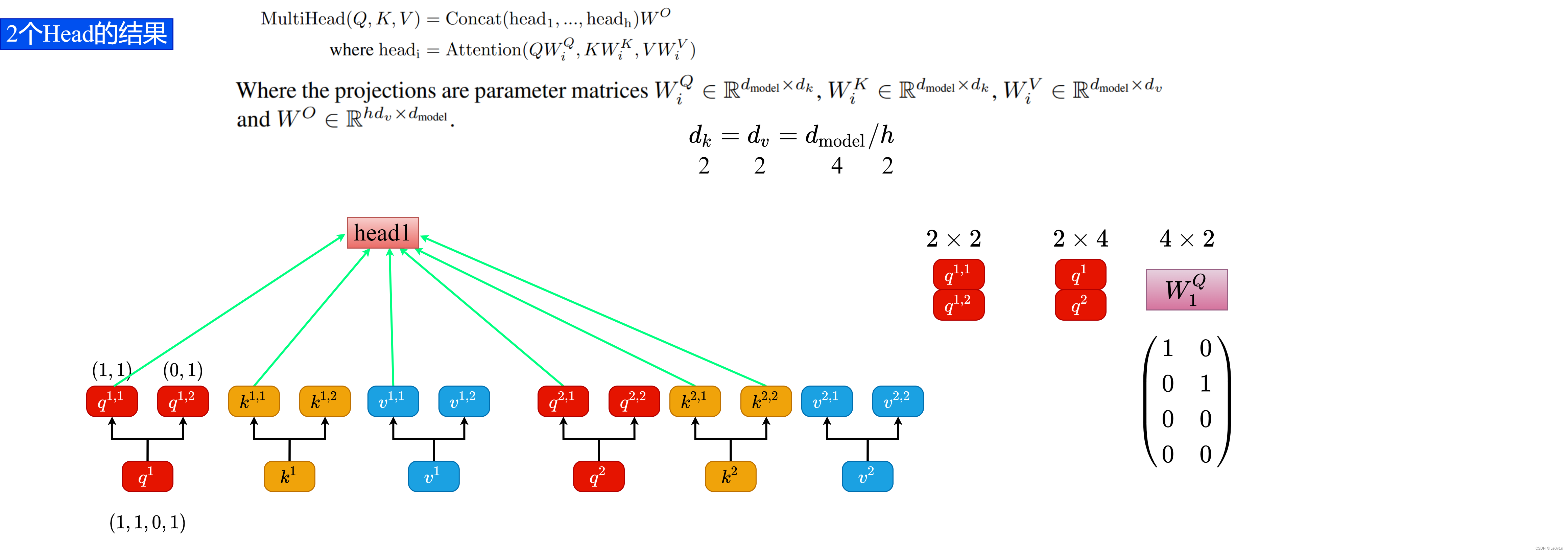
下图中的 Q Q Q 通过 W 1 Q W^Q_1 W1Q 就能得到均分后的 Q 1 Q_1 Q1。
将输入 q i , k i , v i q^i, k^i, v^i qi,ki,vi 按照 h e a d head head 个数拆分后,看第二个数字。第二个数字表明该向量的所属的头(head)。
所以我们将
q
1
,
1
,
k
1
,
1
,
v
1
,
1
q^{1, 1}, k^{1, 1}, v^{1, 1}
q1,1,k1,1,v1,1 和
q
2
,
1
,
k
2
,
1
,
v
2
,
1
q^{2,1}, k^{2, 1}, v^{2, 1}
q2,1,k2,1,v2,1 都归属于
h
e
a
d
1
head_1
head1。
将
q
1
,
2
,
k
1
,
2
,
v
1
,
2
q^{1, 2}, k^{1, 2}, v^{1, 2}
q1,2,k1,2,v1,2 和
q
2
,
2
,
k
2
,
2
,
v
2
,
2
q^{2,2}, k^{2, 2}, v^{2, 2}
q2,2,k2,2,v2,2 都归属于
h
e
a
d
2
head_2
head2。
在原论文中,这个过程如下:
( q 1 , 1 q 2 , 1 ) = ( q 1 q 2 ) W 1 Q \binom{q^{1, 1}}{q^{2, 1}} = \binom{q^1}{q^2} W_1^Q (q2,1q1,1)=(q2q1)W1Q
但是在实际处理中,没有什么线性映射,就是一个均分操作。所以我们可以将 W 1 Q W_1^Q W1Q 写成如下的形式:
( q 1 , 1 q 2 , 1 ) = ( q 1 q 2 ) W 1 Q = ( q 1 q 2 ) ( 1 0 0 1 0 0 0 0 ) \begin{aligned} \binom{q^{1, 1}}{q^{2, 1}} & = \binom{q^1}{q^2} W_1^Q \\ & = \binom{q^1}{q^2} \left(\begin{matrix}1 & 0 \cr 0 & 1 \cr 0 & 0 \cr 0 & 0\end{matrix}\right) \end{aligned} (q2,1q1,1)=(q2q1)W1Q=(q2q1)⎝⎜⎜⎛10000100⎠⎟⎟⎞
这样定义 W 1 Q W_1^Q W1Q 就可以实现均分的操作。
同理, k , v k, v k,v 也可以这样操作。
( q 1 , 1 q 2 , 1 ) = ( q 1 q 2 ) ( 1 0 0 1 0 0 0 0 ) ( k 1 , 1 k 2 , 1 ) = ( k 1 k 2 ) ( 1 0 0 1 0 0 0 0 ) ( v 1 , 1 v 2 , 1 ) = ( v 1 k 2 ) ( 1 0 0 1 0 0 0 0 ) \begin{aligned} &\binom{q^{1, 1}}{q^{2, 1}} = \binom{q^1}{q^2} \left(\begin{matrix}1 & 0 \cr 0 & 1 \cr 0 & 0 \cr 0 & 0\end{matrix}\right) \\ &\binom{k^{1, 1}}{k^{2, 1}} = \binom{k^1}{k^2} \left(\begin{matrix}1 & 0 \cr 0 & 1 \cr 0 & 0 \cr 0 & 0\end{matrix}\right) \\ &\binom{v^{1, 1}}{v^{2, 1}} = \binom{v^1}{k^2} \left(\begin{matrix}1 & 0 \cr 0 & 1 \cr 0 & 0 \cr 0 & 0\end{matrix}\right) \end{aligned} (q2,1q1,1)=(q2q1)⎝⎜⎜⎛10000100⎠⎟⎟⎞(k2,1k1,1)=(k2k1)⎝⎜⎜⎛10000100⎠⎟⎟⎞(v2,1v1,1)=(k2v1)⎝⎜⎜⎛10000100⎠⎟⎟⎞
这里的 W 1 Q ∈ R 4 × 2 W_1^Q \in {\mathbb R}^{4 \times 2} W1Q∈R4×2 的原因是 ( q 1 q 2 ) ∈ R 2 × 4 \binom{q^1}{q^2} \in {\mathbb R}^{2 \times 4} (q2q1)∈R2×4(因为我们之前假设 q i , k i , v i q^i, k^i, v^i qi,ki,vi 的向量长度为 4 4 4),而我们想要根据 h e a d head head 进行均分,所以需要让 W 1 Q ∈ R 4 × 2 W_1^Q \in {\mathbb R}^{4 \times 2} W1Q∈R4×2 才能满足条件。
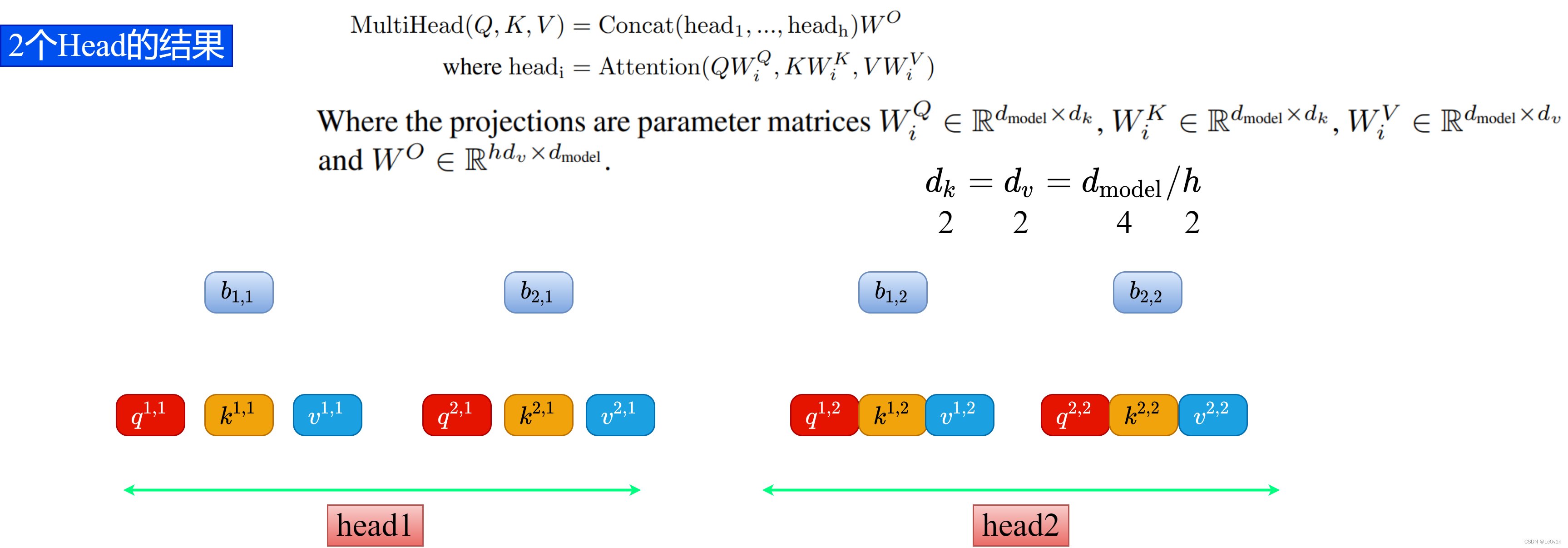
接下来每个 h e a d i head_i headi 各自执行Self-Attention就可以得到每个 h e a d i head_i headi 对应的 b j , i b_{j,i} bj,i 了。计算公式和Self-Attention是一样的,如下所示。
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V {\rm Attention}(Q, K, V) = {\rm softmax}(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dkQKT)V
其实这里对应的公式应该MSA中的:
w h e r e h e a d i = A t t e n t i o n ( Q W i Q , K W i K , V W i V ) {\rm where \ head_i = Attention}(QW_i^Q, KW_i^K, VW_i^V) where headi=Attention(QWiQ,KWiK,VWiV)
过程如下图所示。
在得到每个 head 的输出
b
j
,
i
b_{j, i}
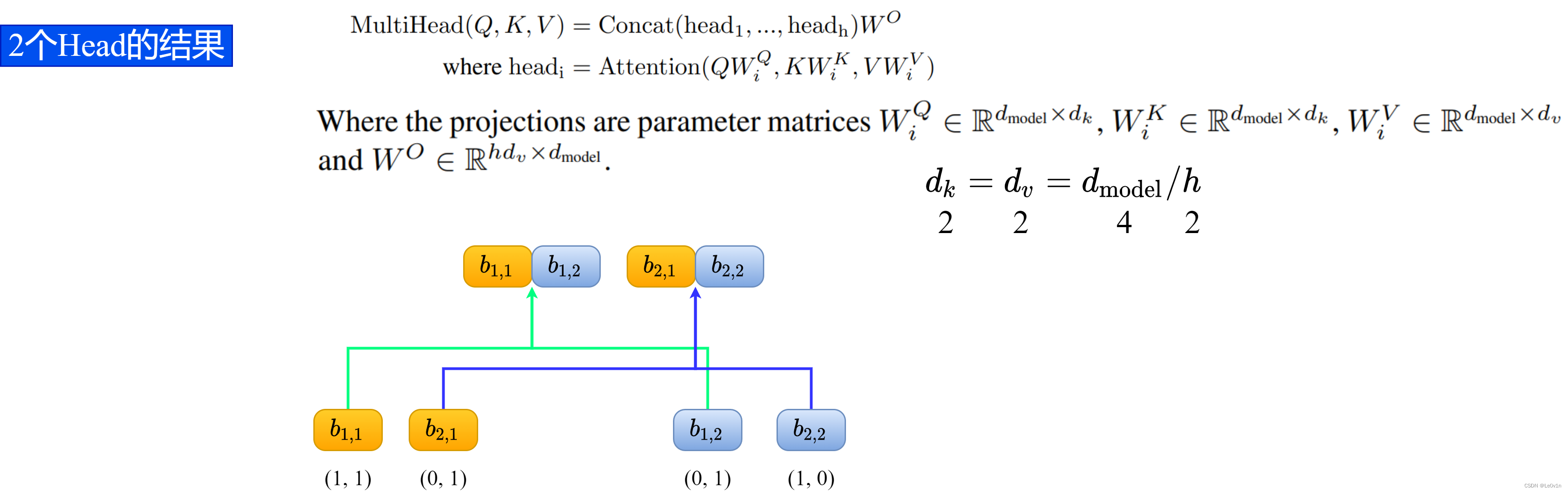
bj,i 后,需要对每个head的结果进行 Concat 拼接。
- b 1 , 1 b_{1,1} b1,1( h e a d 1 head_1 head1 得到的 b 1 b_1 b1)和 b 1 , 2 b_{1,2} b1,2( h e a d 2 head_2 head2得到的 b 1 b_1 b1)拼接在一起
- b 2 , 1 b_{2,1} b2,1( h e a d 1 head_1 head1 得到的 b 2 b_2 b2)和 b 2 , 2 b_{2,2} b2,2( h e a d 2 head_2 head2 得到的 b 2 b_2 b2)拼接在一起
拼接过程如下图所示:
可以看到,这里并不是按第二个数字走的(所属head),而是按第一个数字走的(原来向量的编号)。
不按第二个数字走,说明是不同的 head 输出拼在了一起。
这样的拼接操作可以理解为多头信息交流。
(多头只是为了特征提取)
这也就对应公式:
M u l t i H e a d ( Q , K , V ) = C o n c a t ( h e a d 1 , . . . , h e a d h ) ) {\rm MultiHead}(Q, K, V) = {\rm Concat(head_1, ..., head_h))} MultiHead(Q,K,V)=Concat(head1,...,headh))
接着将拼接后的结果通过 W O W^O WO(可学习的参数)进行融合,得到MSA的最终输出 b 1 , b 2 b_1, b_2 b1,b2,过程如下图所示。
注意:这里的 W O W^O WO 的shape为 h d v × d m o d e l hd_v \times d_{\rm model} hdv×dmodel。
其中:
- h h h 为MSA h e a d head head 的个数
- d v d_v dv 为 v v v 的向量长度
- d m o d e l d_{\rm model} dmodel 为 MSA 输入向量的长度(在前面图中举例时,我们假设 q i , k i , v i q^i, k^i, v^i qi,ki,vi 的向量长度为 4 4 4)
前面我们说过了,在MSA中, q , k , v q, k, v q,k,v 在实际操作中都是通过简单粗暴地按照 h e a d head head 和个数( h h h) 进行均分的,所以 d q b e f o r e s p l i t e d = d k b e f o r e s p l i t e d = d v b e f o r e s p l i t e d = d m o d e l d^{\rm before \ splited}_q = d^{\rm before \ splited}_k = d^{\rm before \ splited}_v = d_{\rm model} dqbefore splited=dkbefore splited=dvbefore splited=dmodel。于是乎, h × d v a f t e r s p l i t e d = d m o d e l h \times d^{\rm after\ splited}_v = d_{\rm model} h×dvafter splited=dmodel。故,这里 W O W^O WO 的shape其实就是 R d m o d e l × d m o d e l {\mathbb R}^{d_{\rm model} \times d_{\rm model}} Rdmodel×dmodel。
根据文中的假设, d m o d e l = 4 d_{\rm model} = 4 dmodel=4,所以 W O ∈ R 4 × 4 W^O \in {\mathbb R}^{4\times 4} WO∈R4×4。
这里我们假设 W O W^O WO 中的内容为:
W O = ( 1 , 1 , 0 , 0 0 , 1 , 0 , 1 1 , 0 , 1 , 1 0 , 1 , 0 , 0 ) W^O = \left( \begin{matrix} 1, 1, 0, 0 \\ 0, 1, 0, 1 \\ 1, 0, 1, 1\\ 0, 1, 0, 0 \end{matrix} \right) WO=⎝⎜⎜⎛1,1,0,00,1,0,11,0,1,10,1,0,0⎠⎟⎟⎞
前面我们将不同head的Self-Attention的结果并行了Concat处理,得到:
b = ( b 1 , 1 , b 1 , 2 b 2 , 1 , b 2 , 2 ) = ( 1 , 1 , 0 , 1 0 , 1 , 1 , 0 ) b = \binom{b_{1, 1}, b_{1, 2}}{b_{2, 1}, b_{2, 2}} = \binom{1, 1, 0, 1}{0, 1, 1, 0} b=(b2,1,b2,2b1,1,b1,2)=(0,1,1,01,1,0,1)
从这里的结果可以看到,前面Concat是跟着第一个数字走的,而不是第二个数字head走的。目的就是为了不同头之间的信息交流。
那么我们就可以得出MSA的最终输出:
( b 1 b 2 ) = ( 1 , 1 , 0 , 1 0 , 1 , 1 , 0 ) ( 1 , 1 , 0 , 0 0 , 1 , 0 , 1 1 , 0 , 1 , 1 0 , 1 , 0 , 0 ) = ( 1 , 3 , 0 , 1 1 , 1 , 1 , 2 ) \begin{aligned} \binom{b_1}{b_2} & = \binom{1, 1, 0, 1}{0, 1, 1, 0} \left( \begin{matrix} 1, 1, 0, 0 \\ 0, 1, 0, 1 \\ 1, 0, 1, 1\\ 0, 1, 0, 0 \end{matrix} \right) \\ & = \binom{1, 3, 0, 1}{1, 1, 1, 2} \end{aligned} (b2b1)=(0,1,1,01,1,0,1)⎝⎜⎜⎛1,1,0,00,1,0,11,0,1,10,1,0,0⎠⎟⎟⎞=(1,1,1,21,3,0,1)
这里的MSA其实和组卷积(Group Convolution)非常像。组卷积根据我们设置的group数,在channel维度将特征图拆分为group个组后,对于每个组再进行普通的卷积。
这里的MSA看起来和组卷积差不多,因为 h e a d head head 的存在,输入向量被分为一个个组(确切来说是头 h e a d head head),以 h e a d head head 分组后再进行Self-Attention。将结果进行Concat处理后通过一个可学习的矩阵 W O W^O WO 后得到MSA的最终输出。
到这,Multi-Head Attention的内容就讲完了。总结下来就是论文中的两个公式:
M u l t i H e a d ( Q , K , V ) = C o n c a t ( h e a d 1 , . . . , h e a d h ) W O w h e r e h e a d i = A t t e n t i o n ( Q W i Q , K W i K , V W i V ) {\rm MultiHead}(Q,K,V) = {\rm Concat}({\rm head_1, ..., head_h})W^O \\ {\rm where \ head_i} = {\rm Attention}(QW_i^Q, KW_i^K, VW_i^V) MultiHead(Q,K,V)=Concat(head1,...,headh)WOwhere headi=Attention(QWiQ,KWiK,VWiV)
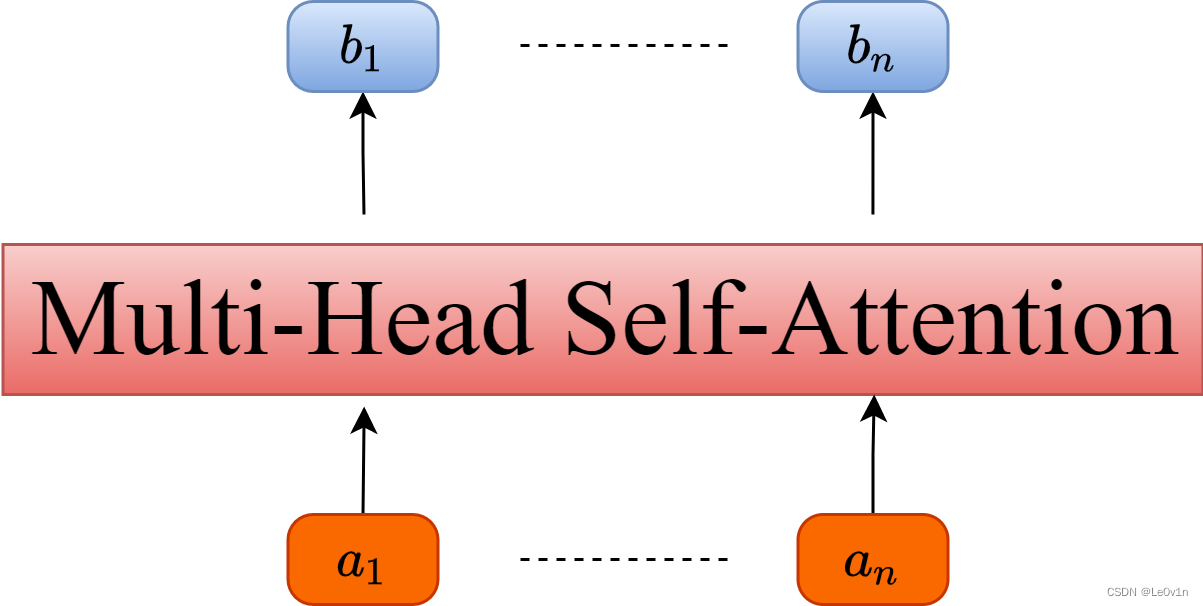
像Self-Attention那样,我们也将MSA抽象为一个模块,如下图所示。
和Self-Attention其实差不多,但MSA使用到了多个Self-Attention。但同样是输入多个向量 a i a_i ai,得到多个输出向量 b i b_i bi。
3. Self-Attention与Multi-Head Attention计算量对比
在原论文章节3.2.2中最后有说两者的计算量其实差不多。
Due to the reduced dimension of each head, the total computational cost is similar to that of single-head attention with full dimensionality.
由于每个头的维度减少,总的计算成本与全维度的单头Self-Attention相似。
下面做了个简单的实验,这个model文件大家先忽略哪来的。这个Attention就是实现Multi-head Attention的方法,其中包括上面讲的所有步骤。
- 首先创建了一个Self-Attention模块(单头)
a1,然后把proj变量置为Identity(Identity对应的是Multi-Head Attention中最后那个 W o W^o Wo 的映射,单头中是没有的,所以置为Identity即不做任何操作)。 - 再创建一个Multi-Head Attention模块(多头)
a2,然后设置8个head。 - 创建一个随机变量,注意shape
- 使用
fvcore分别计算两个模块的FLOPs
import torch
from fvcore.nn import FlopCountAnalysis, parameter_count_table
from vit_model import Attention
def main():
# Self-Attention
a1 = Attention(dim=512, num_heads=1)
a1.proj = torch.nn.Identity() # remove Wo
# Multi-Head Attention
a2 = Attention(dim=512, num_heads=8)
# [batch_size, num_tokens, total_embed_dim]
t = (torch.rand(32, 1024, 512),)
flops1 = FlopCountAnalysis(a1, t) # 1879.0482
print(f"Self-Attention MFLOPs(bs=1): {(flops1.total() / 1000000) / 32:.4f}")
flops2 = FlopCountAnalysis(a2, t) # 2147.4836
print(f"Multi-Head Attention MFLOPs(bs=1): {(flops2.total() / 1000000) / 32:.4f}")
if __name__ == '__main__':
main()
终端输出如下, 可以发现确实两者的MFLOPs差不多,Multi-Head Attention比Self-Attention略高一点:
Self-Attention MFLOPs(bs=1): 1879.0482
Multi-Head Attention MFLOPs(bs=1): 2147.4836
其实两者MFLOPs的差异只是在最后的
W
O
W^O
WO 上,如果把Multi-Head Attentio的
W
O
W^O
WO 也删除(即把 a2 的proj也设置成Identity),可以看出两者MFLOPs是一样的:
Self-Attention MFLOPs(bs=1): 1879.0482
Multi-Head Attention MFLOPs(bs=1): 1879.0482
4. Positional Encoding
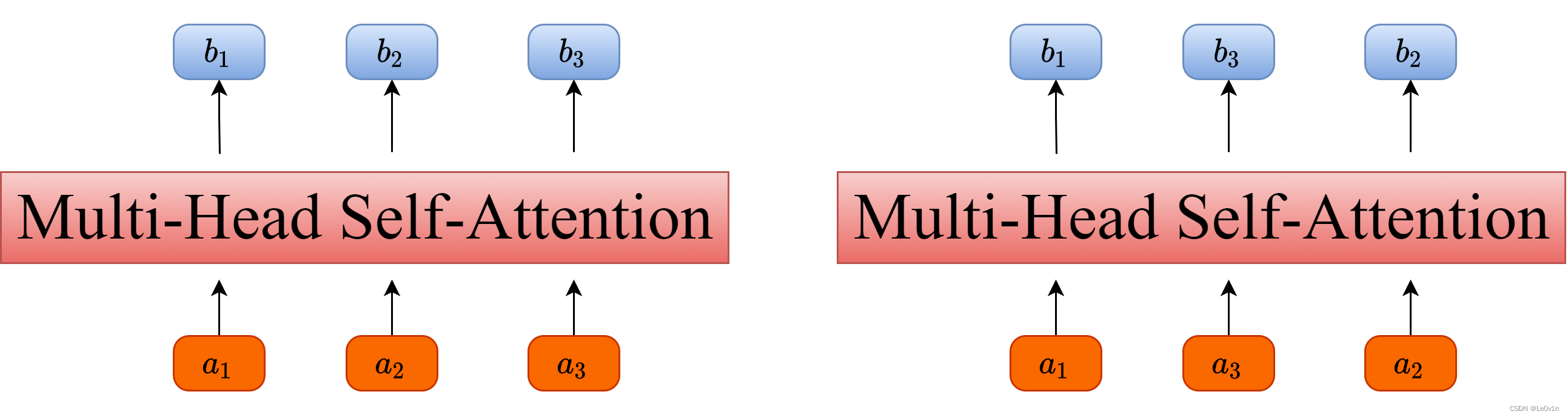
如果仔细观察刚刚讲的Self-Attention和Multi-Head Attention模块,在计算中是没有考虑到位置信息的。假设在Self-Attention模块中,输入
a
1
,
a
2
,
a
3
a_1, a_2, a_3
a1,a2,a3 得到
b
1
,
b
2
,
b
3
b_1, b_2, b_3
b1,b2,b3(即为最终输出)。对于
a
1
a_1
a1 而言,
a
2
a_2
a2 和
a
3
a_3
a3 离它都是一样近的而且没有先后顺序。假设将输入的顺序改为
a
1
,
a
3
,
a
2
a_1, a_3, a_2
a1,a3,a2,对
b
1
b_1
b1 的结果是没有任何影响的。
下面是使用PyTorch做的一个实验,首先使用nn.MultiheadAttention创建一个Self-Attention模块(num_heads=1),注意这里在正向传播过程中直接传入
Q
K
V
QKV
QKV,接着创建两个顺序不同的
Q
K
V
QKV
QKV 变量
t
1
t_1
t1 和
t
2
t_2
t2(主要是将
q
2
,
k
2
,
v
2
q^2, k^2, v^2
q2,k2,v2 和
q
3
,
k
3
,
v
3
q^3, k^3, v^3
q3,k3,v3 的顺序换了下),分别将这两个变量输入Self-Attention模块进行正向传播。
import torch
import torch.nn as nn
# MSA在PyTorch的nn模块中已经集成
m = nn.MultiheadAttention(embed_dim=2, num_heads=1)
t1 = [[[1., 2.], # q1, k1, v1
[2., 3.], # q2, k2, v2
[3., 4.]]] # q3, k3, v3
t2 = [[[1., 2.], # q1, k1, v1
[3., 4.], # q3, k3, v3
[2., 3.]]] # q2, k2, v2
q, k, v = torch.as_tensor(t1), torch.as_tensor(t1), torch.as_tensor(t1)
print("result1: \n", m(q, k, v))
q, k, v = torch.as_tensor(t2), torch.as_tensor(t2), torch.as_tensor(t2)
print("result2: \n", m(q, k, v))
对比结果可以发现,即使调换了 q 2 , k 2 , v 2 q^2, k^2, v^2 q2,k2,v2 和 q 3 , k 3 , v 3 q^3, k^3, v^3 q3,k3,v3 的顺序,但对于 b 1 b_1 b1 的结果是没有影响的。
result1:
(tensor([[[-0.5824, 0.0231],
[-0.7081, 0.2407],
[-0.8337, 0.4583]]], grad_fn=<AddBackward0>), tensor([[[1.]],
[[1.]],
[[1.]]], grad_fn=<DivBackward0>))
result2:
(tensor([[[-0.5824, 0.0231],
[-0.8337, 0.4583],
[-0.7081, 0.2407]]], grad_fn=<AddBackward0>), tensor([[[1.]],
[[1.]],
[[1.]]], grad_fn=<DivBackward0>))
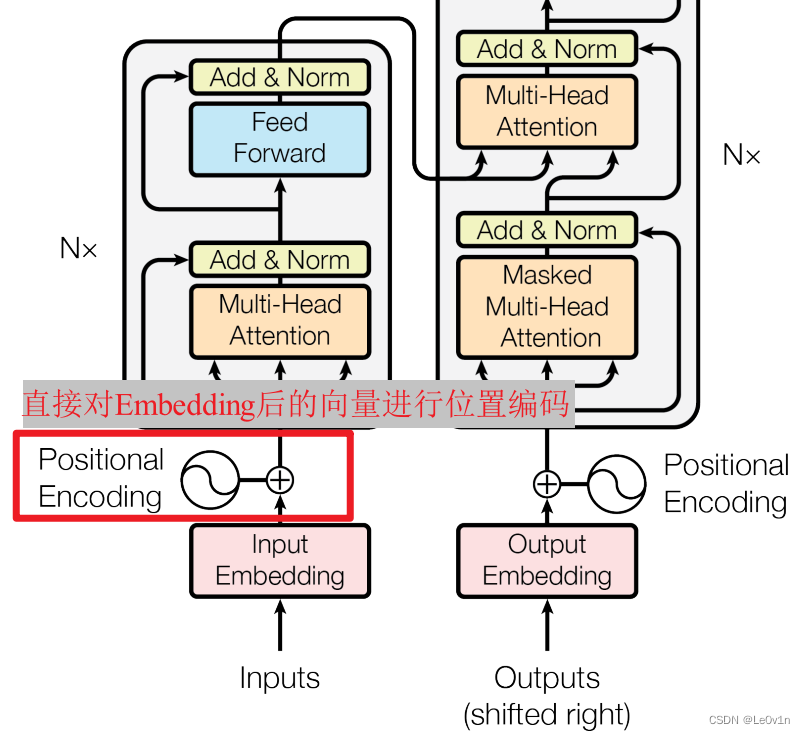
为了解决该问题,论文中提出了一种“位置编码(Position Encoding)”的思想。实现过程比较简单:对应每一个输入 a i a_i ai 都会加上一个 p e i pe_i pei。这里的 p e i pe_i pei 对应的是“位置编码”。
To this end, we add “positional encodings” to the input embeddings at the bottoms of the encoder and decoder stacks.
如下图所示,位置编码是直接加在输入的 a = { a 1 , . . . , a n } a=\{a_1,...,a_n\} a={a1,...,an} 中的,即 p e = { p e 1 , . . . , p e n } pe=\{pe_1,...,pe_n\} pe={pe1,...,pen} 和 a = { a 1 , . . . , a n } a=\{a_1,...,a_n\} a={a1,...,an} 拥有相同的维度大小。
那么这个 p e i pe_i pei 是怎么求得呢?
关于位置编码在原论文中有提出两种方案:
- 一种是原论文中使用的固定编码,即论文中给出的
sine and cosine functions方法,按照该方法可计算出位置编码 - 另一种是可训练(可学习的)的位置编码
作者说尝试了两种方法发现结果差不多(但在ViT论文中使用的是可训练的位置编码)
5. 超参数对比
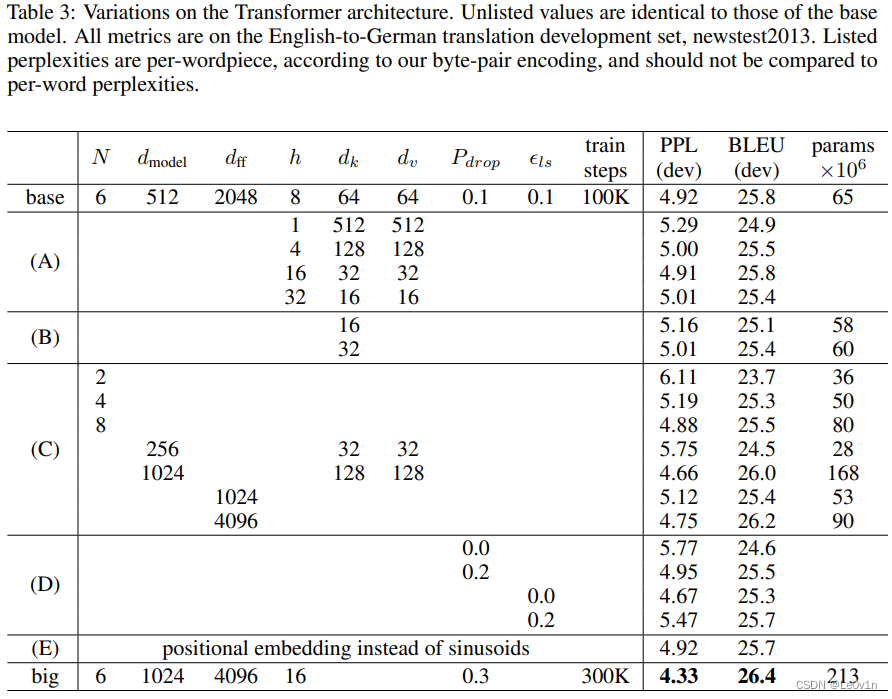
关于Transformer中的一些超参数的实验对比可以参考原论文的表3,如下图所示。
表3:Transformer结构的变化。未列出的数值与基本模型的数值相同。所有指标都是在
英德翻译开发集newstest2013上得到的。根据我们的字节对编码,列出的perplexities是per-wordpiece计算的,不应该与per-word计算的perplexities进行比较。
其中:
- N N N 表示重复堆叠Transformer Block的次数
- d m o d e l d_{\rm model} dmodel 表示Multi-Head Self-Attention输入输出的 t o k e n token token 维度(向量长度) -> 因为这里的MSA是一个注意力模块,一般而言,注意力模块不会对特征图的shape造成影响。
- d f f d_{\rm ff} dff表示在MLP(feed forward)中隐层的节点个数
- h h h表示Multi-Head Self-Attention中 h e a d head head的个数
- d k , d v d_k, d_v dk,dv 表示Multi-Head Self-Attention中每个head的 k e y ( K ) key(K) key(K) 以及 q u e r y ( Q ) query(Q) query(Q) 的维度
-
P
d
r
o
p
P_{\rm drop}
Pdrop 表示
dropout层的drop_rate - ϵ l s \epsilon_{ls} ϵls为Label Smoothing的大小
- train steps为训练batch的个数
到这里,关于Self-Attention、Multi-Head Attention以及位置编码的内容就全部讲完了。
知识来源
- https://blog.csdn.net/qq_37541097/article/details/117691873
- https://www.bilibili.com/video/BV15v411W78M