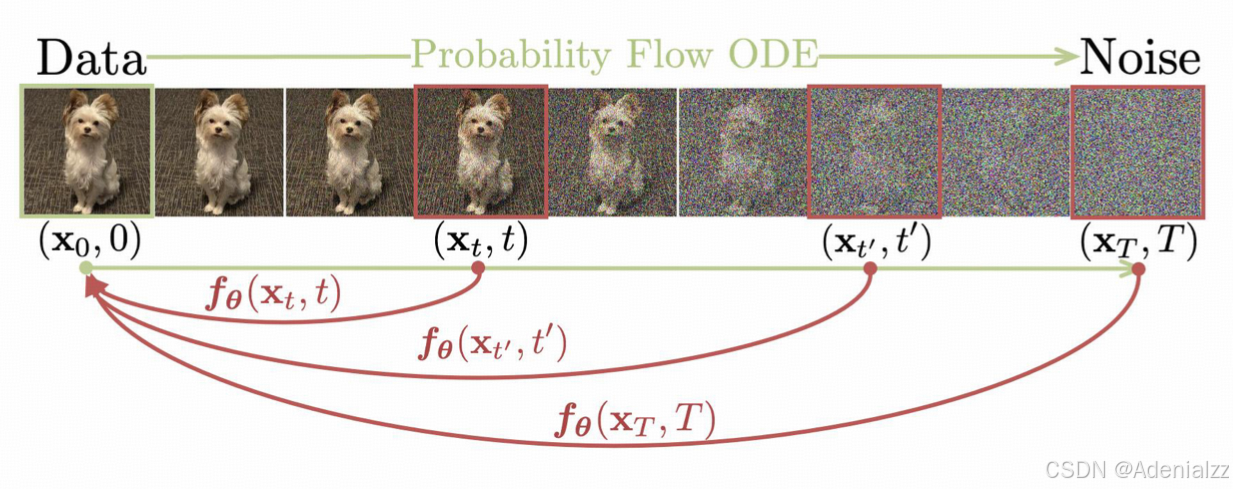
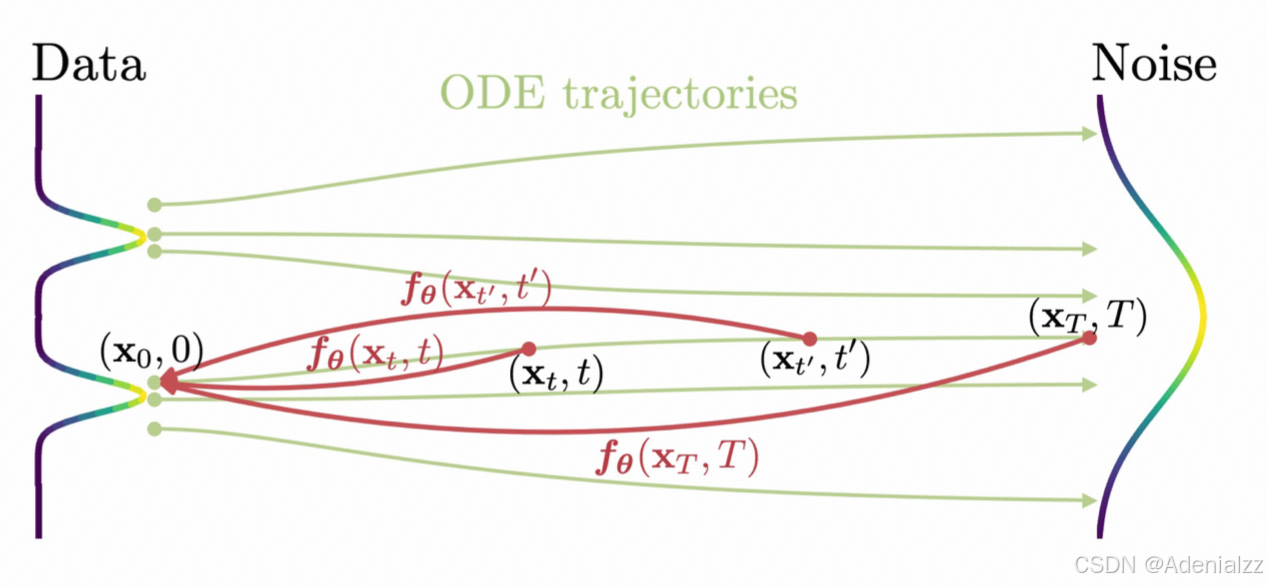
Consistency Models

本文介绍 Song Yang 大佬提出的 Consistency Models，实现扩散模型一步采样生成，同时支持多步采样以权衡采样质量和生成速度。可通过蒸馏或原生训练两种模式进行训练。

背景知识：扩散模型

Consistency Models 的设计是基于连续时间扩散模型（SDE/ODE、EDM）。扩散模型通过高斯噪声扰动，逐步将数据转变为纯噪声，并通过从纯噪声图逐步去噪来生成新的样本。具体来说，记数据分布为 $p_{\text{data}}(\mathbf{x})$，扩散模型首先使用 Ito SDE 对其进行扰动：
$$d{\mathbf{x}}_t=\mu ({\mathbf{x}}_t,t)dt+\sigma (t)d{\mathbf{w}}_t$$
其中 $t\in [0,T]$，$T>0$ 是一个常数，$\mu (\cdot ,\cdot )$ 和 $\sigma (t)$ 分别是漂移系数和扩散系数， { w t } t ∈ [ 0 , T ] \{\mathbf{w}_t\}_{t\in[0,T]} {wt​}t∈[0,T]​ 表示标准布朗运动。我们记 ${\mathbf{x}}_t$ 的分布为 $p_t(\mathbf{x})$，从而有 $p_0(\mathbf{x})\equiv p_{\text{data}}(\mathbf{x})$。这个 SDE 有一个很关键的性质，即：存在一个 ODE（称为概率流 ODE，PF ODE），其解轨迹在 $t$ 时刻的采样也服从同样的 $p_t(\mathbf{x})$。该 ODE 的形式为：
$$d{\mathbf{x}}_t=[\mu ({\mathbf{x}}_t,t)-\frac{1}{2}\sigma (t{)}^2\nabla \log p_t({\mathbf{x}}_t)]dt$$
其中 $\log p_t(\mathbf{x})$ 是分布 $p_t(\mathbf{x})$ 的得分函数。因此扩散模型同样也可以看作是基于得分的生成模型。可以看到，在 PF ODE 中，只有得分函数 $\nabla \log p_t(\mathbf{x})$ 是未知的，因此我们只需要训练一个得分模型 ${\mathbf{s}}_{\varphi }(\mathbf{x},t)\approx \nabla \log p_t(\mathbf{x})$ 来估计各时刻分布的得分，就可以根据 PF ODE 进行采样生成。

一般来说，公式 1 中我们选定的的 SDE 形式需要满足在 $t=T$ 时刻的分布 $p_T(\mathbf{x})$ 接近于一个便于计算的高斯分布 $\pi (\mathbf{x})$。满足这个条件的 SDE 形式有很多，本文中采用的是 EDM 中的 SDE 形式，即 $\mu (\mathbf{x},t)=0$、$\sigma (t)=\sqrt{2t}$。在此形式下，各时刻的分布可表示为数据分布与一个高斯分布的卷积的形式：$p_t(\mathbf{x})=p_{\text{data}}(\mathbf{x})⨂\mathcal{N}(0,t^2\mathbf{I})$，其中 $⨂$ 表示卷积操作，$\pi (\mathbf{x})$ 服从高斯分布 $\pi (\mathbf{x})\sim \mathcal{N}(0,T^2\mathbf{I})$。在 EDM 的形式下，PF ODE 为：
$$\frac{d{\mathbf{x}}_t}{dt}=-t{\mathbf{s}}_{\varphi }({\mathbf{x}}_t,t)$$
我们将上式称为 empirical PF ODE。在采样时，我们首先采样最后一个时刻的 ${\hat{\mathbf{x}}}_T\sim \pi =\mathcal{N}(0,T^2\mathbf{I})$ 来对 empirical PF ODE 进行初始化，然后使用数值 ODE 求解器（如 Euler、Heun 等）按照反向时间来对其进行求解。会得到各时刻解组成的解轨迹 { x ^ t } t ∈ [ 0 , T ] \{\hat{\mathbf{x}}_t\}_{t\in[0,T]} {x^t​}t∈[0,T]​。解轨迹的最后一步 ${\hat{\mathbf{x}}}_0$ 就可以认为是大致服从数据分布 $p_{\text{data}}(\mathbf{x})$ 的样本。为了提高数值稳定性，一个常用的技巧是在时间到达一个很小的值 $t=ϵ$ 处就停止（而不是达到 0），将 ${\hat{\mathbf{x}}}_{ϵ}$ 作为最终的生成结果。参考 EDM 中的经验，我们将像素值 rescale 到 $[-1,1]$ 之间，并设 $T=80,ϵ=0.002$​。

目前，扩散模型应用的主要瓶颈在于采样生成速度。可以看到，使用 ODE 求解器进行采样生成需要多次对得分模型进行计算，这样计算开销很大。现在已经有一些方法，从数值 ODE 求解器加速和蒸馏等方面加速扩散模型采样。然而，目前 ODE 求解器再怎么也需要至少 10 步的模型计算，而大多数蒸馏的方法收集扩散模型生图的大规模数据集。目前只有 Progressive Distillation 没有这个限制，这也是本文对比的主要方法。

Consistency Models

本文提出的 Consistency Model，从设计上就支持单步生成，同时也支持多步采样，使得我们能够在采样速度和生成质量上进行灵活权衡。CM 有两种训练模式：蒸馏模式和原生训练模式。在蒸馏模式中，CM 可以对一个预训练的扩散模型进行知识蒸馏，得到一个单步采样器，对比其他蒸馏加速采样的方法，生图质量大大提升，并且还可以进行 zeroshot 图像编辑。在原生训练模式中，不需要先有一个预训练的扩散模型，直接从头训练 CM，这样 CM 相当于是一类全新的生成模型。

以下，我们将从定义、参数化、采样、图像编辑三个方面介绍 Consistency Model，下一章介绍 Consistency Model 的两种训练模式。

定义

给定一个 PF ODE 的解轨迹 { x t } t ∈ [ ϵ , T ] \{\mathbf{x}_t\}_{t\in[\epsilon,T]} {xt​}t∈[ϵ,T]​，我们定义一个一致性函数 $f:({\mathbf{x}}_t,t)\to {\mathbf{x}}_{ϵ}$。一致性函数有一个重要的性质：自一致性，即对于同一个 PF ODE 解轨迹中的任意的输入参数对 $({\mathbf{x}}_t,t)$，其输出是一致的。自一致性可表示为：对于所有的 $t,t^{\prime }\in [ϵ,T]$，都有 $f({\mathbf{x}}_t,t)=f({\mathbf{x}}_{t^{\prime }},t^{\prime })$。我们的 Consistency Model $f_{\theta }$ 就是要通过学习出自一致性，来拟合这个一致性函数 $f$​。

参数化

满足自一致性的一致性函数，一定有一个边界条件：$f({\mathbf{x}}_{ϵ},ϵ)={\mathbf{x}}_{ϵ}$，即不管输入是什么， $f(\cdot ,ϵ)$ 是一个恒等映射。所有的一致性函数都需要满足这个边界条件，这是 CM 成功训练的关键，也是 CM 在结构上的一种限制。对于基于神经网络的 CM，我们讨论两种满足边界条件的形式。假设我们有一个输入输出的维度相同的、无任何限制的神经网络 $F_{\theta }(\mathbf{x},t)$。

第一种满足边界条件的形式是直接将 CM 参数化为：
$$f_{\theta }(\mathbf{x},t)=\{\begin{array}{ll}\mathbf{x}& t=ϵ\\ F_{\theta }(\mathbf{x},t)& t\in (ϵ,T)\end{array}$$
第二种参数化的形式是使用跳跃连接（skip connections）：
$$f_{\theta }(\mathbf{x},t)=c_{\text{skip}}(t)\mathbf{x}+c_{\text{out}}{F}_{\theta }(\mathbf{x},t)$$
其中 $c_{\text{skip}}(t)$ 和 $c_{\text{out}}(t)$ 都是可微函数，且有 $c_{\text{skip}}(ϵ)=1,c_{\text{out}}(ϵ)=0$。这样，也能满足边界条件。我们注意到，第二种 CM 的参数化形式与 EDM、eDiff-i 等扩散模型的形式非常像，有许多可以借鉴的模型结构。因此我们选择第二种参数化形式。

采样

当一致性模型 $f_{\theta }(\cdot ,\cdot )$ 训练完成之后，我们就可以进行采样生成样本。只需先从初始化分布中采样一个 ${\hat{\mathbf{x}}}_T\sim \mathcal{N}(0,T^2\mathbf{I})$ ，然后可以使用一致性模型直接得到生成结果 ${\hat{\mathbf{x}}}_{ϵ}=f_{\theta }({\hat{\mathbf{x}}}_T,T)$​。这仅需要一次 Consistency Model 的前向推理过程。同时，我们也可以选择执行多次推理，交替进行去噪和噪声注入，来实现多步生成。

具体来说，多步采样的过程如以下算法 1 所示。首先使用 CM 根据 ${\hat{\mathbf{x}}}_T$ 一步生成，初始化一个预测的数据样本 $\mathbf{x}$，然后将这个 $\mathbf{x}$ 加噪成中间步 ${\tau }_n$ 的噪声图，然后再用 CM 对这一步的噪声图进行一步生成，得到新的预测数据样本 $\mathbf{x}$。然后不断重复交替进行加噪、去噪的过程共 $N$ 次，得到最终 $N$​​ 步的生成结果。

通过多步生成，我们可以提高提升生成结果的质量。这样，我们就能灵活地在采样速度和样本质量之间进行权衡。

这里有一个示意图，将 CM 多步采样的过程清楚地展示了出来。图片来源：Consistency is All You Need。

蒸馏训练 CM

我们首先介绍第一种训练 CM 的方法：对一个预训练的得分模型 ${\mathbf{s}}_{\varphi }(\mathbf{x},t)$ 进行蒸馏。我们还是围绕公式 3 中的 empirical PF ODE 展开讨论，将时间区间 $[ϵ,T]$ 离散化为 $N-1$ 个子区间，边界分别为 $t_1=ϵ<t_2<\cdots <t_N=T$。在实现中，我们参考 EDM 中的公式来确定区间边界 $t_i=({ϵ}^{1/\rho }+\frac{i-1}{N-1}(T^{1/\rho }-{ϵ}^{1-\rho }){)}^{\rho }$，其中 $\rho =7$。当 $N$ 足够大时，我们就可以通过执行数值 ODE 求解器的一个离散步，来根据 ${\mathbf{x}}_{t_{n+1}}$ 得到 ${\mathbf{x}}_{t_n}$ 的精确估计值。我们记该估计值为 ${\hat{\mathbf{x}}}_{t_n}^{\varphi }$，具体定义为：
$${\hat{\mathbf{x}}}_{t_n}^{\varphi }:={\mathbf{x}}_{t_{n+1}}+(t_n-t_{n+1})\Phi ({\mathbf{x}}_{t_{n+1}},t_{n+1};\varphi )$$
其中 $\Phi (\dots ;\varphi )$ 表示对 empirical PF ODE 执行一步 ODE 求解器的更新方程。比如说当使用 Euler 求解器时，有 $\Phi (\mathbf{x},t;\varphi )=-t{\mathbf{s}}_{\varphi }(\mathbf{x},t)$，对应于以下更新公式：
$${\hat{\mathbf{x}}}_{t_n}^{\varphi }:={\mathbf{x}}_{t_{n+1}}-(t_n-t_{n+1})t_{n+1}{\mathbf{s}}_{\varphi }({\mathbf{x}}_{t_{n+1}},t_{n+1})$$
简单起见，我们这里先只考虑单步的 ODE 求解器。这里其实就相当于是离散扩散模型根据 ${\mathbf{x}}_{t+1}$ 进行单步去噪得到上一时间步 ${\mathbf{x}}_t$ 的过程。

根据公式 2 PF ODE 与公式 1 SDE 之间的联系，我们可以通过先采样 $\mathbf{x}\sim p_{\text{data}}$，然后向 $\mathbf{x}$ 中添加高斯噪声的方式，来采样出 ODE 轨迹。具体来说，给定一个数据样本 $\mathbf{x}$，根据 SDE 的转移密度 $\mathcal{N}(\mathbf{x},t_{n+1}^2\mathbf{I})$ 采样出 ${\mathbf{x}}_{t_{n+1}}$，然后使用 ODE 求解器的一步更新公式，计算出前一时刻的 ${\hat{\mathbf{x}}}_{t_n}^{\varphi }$，从而我们就能得到相邻时刻的数据点的 pair 对 $({\hat{\mathbf{x}}}_{t_n}^{\varphi },{\mathbf{x}}_{t_{n+1}})$。然后，我们就可以以最小化这个相邻时间步 pair 对一致性输出的差异为训练目标，训练 CM。具体来说，通过蒸馏的方式训练 CM 的 consistency distillation 损失定义为：
$${\mathcal{L}}_{CD}^N(\theta ,{\theta }^{-};\varphi ):=\mathbb{E}[\lambda (t_n)d(f_{\theta }({\mathbf{x}}_{t_{n+1}},t_{n+1}),f_{{\theta }^{-}}({\hat{\mathbf{x}}}_{t_n}^{\varphi },t_n))]$$
这里的期望是关于 $\mathbf{x}\sim p_{\text{data}},n\sim \mathcal{U}[1,N-1],{\mathbf{x}}_{t_{n+1}}\sim \mathcal{N}(\mathbf{x};t_{n+1}^2\mathbf{I})$。其中 $\lambda (\cdot )\in {\mathbb{R}}^{+}$ 是正值加权函数，一般取恒等加权函数 $\lambda (t_n)=1$ 即可。，$d(\cdot ,\cdot )$ 是某种距离度量，文中实验了 L1、L2 和 LPIPS 三种距离。使用随机梯度下降优化 CM 的参数 $\theta$，并使用 EMA 来更新参数 ${\theta }^{-}$，EMA 更新公式为：

$${\theta }^{-}\leftarrow \text{stopgrad}(\mu {\theta }^{-}+(1-\mu )\theta )$$
其中 ${\theta }^{-}$ 是优化过程中滑动平均值的上一步，$0\le \mu <1$。

原生训练 CM

原生训练 CM 时，我们不需要预训练的扩散模型 ${\mathbf{s}}_{\varphi }(\mathbf{x},t)$ 来估计分布得分 $\nabla \log p_t({\mathbf{x}}_t)$ 了。此时，我们可以根据 $\mathbf{x}$ 和 ${\mathbf{x}}_t$ 来估计得分：
$$\nabla \log p_t({\mathbf{x}}_t)=-\mathbb{E}[\frac{{\mathbf{x}}_t-\mathbf{x}}{t^2}|{\mathbf{x}}_t]$$
其中 $\mathbf{x}\sim p_{\text{data}}$，${\mathbf{x}}_t\sim \mathcal{N}(\mathbf{x};t^2\mathbf{I})$。当我们使用 Euler ODE 求解器，在 $N\to \infty$ 时，这个无偏估计足以替代上述蒸馏训练 CM 时的预训练扩散模型，原文定理 2 给出了证明。

consistency training 的目标函数定义为：
$$\mathcal{L}(\theta ,{\theta }^{-}):=\mathbb{E}[\lambda (t_n)d(f_{\theta }(\mathbf{x}+t_{n+1}\mathbf{z},t_{n+1}),f_{{\theta }^{-}}(\mathbf{x}+t_n\mathbf{z},t_n))]$$
注意这里的损失 $\mathcal{L}(\theta ,{\theta }^{-})$ 仅与 CM 参数 $\theta ,{\theta }^{-}$ 有关，与预训练扩散模型参数 $\varphi$ 无关。

总结

本文首先回顾了连续时间 SDE/ODE 扩散模型相关的基础知识，并选定了 EDM 的形式化。然后介绍 Consistency Models，考虑一个一致性函数 $f$，其可以从任意时刻一步映射到一致的结果 ${\mathbf{x}}_{ϵ}$。训练一个神经网络 $f_{\theta }$ 来拟合这个 $f$，即为 CM。CM 可以从纯噪声一步采样得到生成样本，也可以多步采样来均衡生成质量和采样速度。CM 的训练模式有蒸馏和原生训练两种，核心都是构建相邻时刻数据点 pair 对，然后最小化 CM $f_{\theta }$ 对二者输出值的差异，生成一致性的结果。区别在于，蒸馏训练模式使用预训练的扩散模型来得到相邻时刻的 pair 对，而原生训练模式则直接通过扩散模型前向加噪公式来进行无偏估计。