目录

一、数据清洗：

1、数据样本采集（抽样）

2、异常值处理

识别异常值和重复值

直接丢弃（包括重复数据）

集中值指代（除异常值外的均值、中位数、众数等等）

插值

根据不同特征值的具体形式处理

二、特征预处理

1、特征选择——剔除与标注不相关或者冗余的特征

过滤思想（设置过滤的阈值）

包裹思想（递归特征消除法算法—RFE—resave feature elimination）

嵌入思想（正则化——系数反应特征重要程度）

2、特征变换

对指化（缩放尺度，单调性不变）

离散化（将连续变量分成几段bins）

归一化或标准化

数值化

正规化（规范化）——可以反应特征对于标注的影响程度占比

3、特征降维

PCA（无监督降维方法，无需用到标注）

LDA（线性判别式分析Linear Discriminant Analysis）

4、特征衍生

四则运算（加减乘除）

求导或者高阶导数

人工归纳（从经验出发拓展特征维度）

三、具体HR的案例分析

1、数据集的质量大小与数据模型的复杂度呈负相关关系。

2、数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已。

3、提取的特征与建模目的相关。

4、主要内容包括：

• 特征使用：数据的选择；分析可用性
• 特征获取：特征来源；特征存储；
• 特征处理：数据清洗；特征预处理；
• 特征监控：现有特征；探寻新特征；

一、数据清洗：

1、数据样本采集（抽样）

• 样本要具备代表性
• 样本比例要平衡以及样本不平衡时如何处理？
• 尽量考虑全量数据——大数据（数据量大，数据维度广）

2、异常值处理

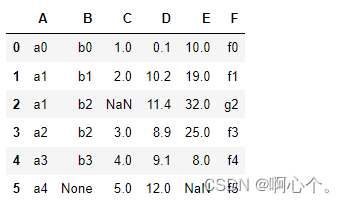
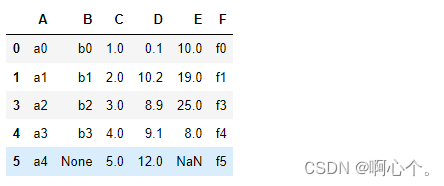
df=pd.DataFrame({"A":["a0","a1","a1","a2","a3","a4"],
                 "B":["b0","b1","b2","b2","b3",None],
                 "C":[1,2,None,3,4,5],
                 "D":[0.1,10.2,11.4,8.9,9.1,12],
                 "E":[10,19,32,25,8,None],
                 "F":["f0","f1","g2","f3","f4","f5"]})

简单构造一组数据：

• 识别异常值和重复值

##识别None值
df.isnull()

##识别特征间的重复值
df.duplicated(["A"])  
df.duplicated(["A","B"])

返回的均为布尔值

 

• 直接丢弃（包括重复数据）

##直接删除包含nan值的整行
df.dropna()

##删除特征“B”中nan的那行
df.dropna(subset=["B"])

##删除重复值所在行
df.drop_duplicates(["A"])  #默认删除第一个

df.drop_duplicates(["A"],keep=False)  
#keep:{"first","last","False"}  （删除第一个；删除最后一个；删除全部重复值）

df.drop_duplicates(["A"],keep=False,inplace=True)  
#inplace=True原始数据会改变，默认为False

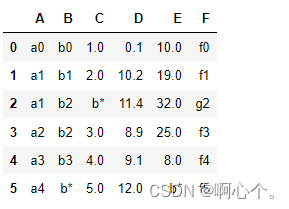
• 集中值指代（除异常值外的均值、中位数、众数等等）

##填充某个值
df.fillna("b*")
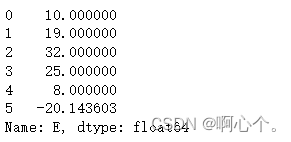
df.fillna(df["E"].mean())  #使用特征“E”的均值

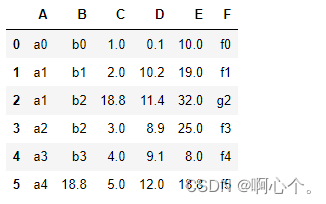
• 插值

df["E"].interpolate()   #插值只能用在series

df["E"].interpolate(method="spline",order=3) #三次样条插值

pd.Series([1,None,4,5,20]).interpolate()

interpolate（）——插值函数https://www.cjavapy.com/article/541/

• 根据不同特征值的具体形式处理

df[[True if item.startswith("f") else False for item in list(df["F"].values)]]
#遍历F中的值，开头字母为f返回True，否则为False。

遍历特征"F"中的值，开头字母为f为正常数据，把第三行数据g2删除。

二、特征预处理

import numpy as np
import pandas as pd
import scipy.stats as ss
df1=pd.DataFrame({"A":ss.norm.rvs(size=10),
                  "B":ss.norm.rvs(size=10),
                  "C":ss.norm.rvs(size=10),
                  "D":np.random.randint(low=0,high=2,size=10)})
df1

生成服从正态分布的三组特征量及一组范围[0,1]的随机整数

1、特征选择——剔除与标注不相关或者冗余的特征

from sklearn.svm import SVR 
from sklearn.tree import DecisionTreeRegressor
#特征选择常用包：过滤思想，包裹思想，嵌入思想
from sklearn.feature_selection import SelectKBest,RFE,SelectFromModel

X=df1.loc[:,["A","B","C"]]
Y=df1.loc[:,"D"]

• 过滤思想（设置过滤的阈值）

过滤思想就是直接评价某个特征与标注的相关性等特征，如果与标注的相关性非常小，就去掉。

skb=SelectKBest(k=2)  #保留k个特征值

#方法一：fit()+transform()
skb.fit(X,Y)

##调用属性scores_，返回得分
skb.scores_
##调用属性pvalues_ ，返回P值
skb.pvalues_   
##返回特征过滤后保留下的特征列索引
skb.get_support(indices=True) 
print(skb.scores_,skb.pvalues_,skb.get_support(indices=True))

##转换数据，得到特征过滤后保留下的特征数据集
skb.transform(X)  

#方法二：fit_transform()
##拟合数据加转化数据一步到位：
x_new=skb.fit_transform(x,y)
x_new

SelectKBest(score_func= f_classif, k=10)

score_func：特征选择要使用的方法，默认适合分类问题的F检验分类：f_classif。
k ：取得分最高的前k个特征，默认10个。

结果：

1、得分： [0.06678612 0.01505405 1.7895258 ]
2、p值：  [0.80259947 0.90537499 0.21776326]
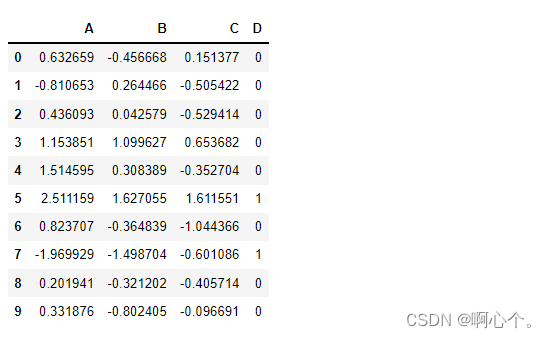
3、特征过滤后保留下来的特征索引： [0 2] ——剔除了第二个特征

4、特征过滤后保留下的特征数据集：

array([[ 0.63265873,  0.15137685],
       [-0.81065328, -0.50542238],
       [ 0.43609265, -0.52941374],
       [ 1.15385088,  0.6536819 ],
       [ 1.5145949 , -0.35270394],
       [ 2.51115888,  1.61155123],
       [ 0.82370728, -1.04436562],
       [-1.96992943, -0.6010865 ],
       [ 0.20194085, -0.40571387],
       [ 0.33187617, -0.09669064]])

• 包裹思想（递归特征消除法算法—RFE—resave feature elimination）

       包裹思想的含义，是我们假设所有的特征是个集合X，最佳的特征组合是它的一个子集。我们的任务就是要找到这个子集。

       递归特征消除（RFE）的主要思想是反复的构建模型（如SVR回归模型）然后选出最好的的特征（可以根据系数来选），把选出来的特征选择出来，然后在剩余的特征上重复这个过程，直到所有特征都遍历了。这个过程中特征被消除的次序就是特征的排序。因此，这是一种寻找最优特征子集的贪心算法。 

rfe=RFE(estimator=SVR(kernel="linear"),n_features_to_select=2,step=1)
rfe.fit_transform(X,Y)

经过递归特征消除法算法保留下的变量：（剔除了第一个特征）

array([[-0.45666814,  0.15137685],
       [ 0.26446625, -0.50542238],
       [ 0.04257889, -0.52941374],
       [ 1.09962668,  0.6536819 ],
       [ 0.30838919, -0.35270394],
       [ 1.62705506,  1.61155123],
       [-0.36483856, -1.04436562],
       [-1.49870357, -0.6010865 ],
       [-0.32120218, -0.40571387],
       [-0.80240473, -0.09669064]])

• 嵌入思想（正则化——系数反应特征重要程度）

       最常见的方法是：对标注建立回归模型，得到特征与标注的权重系数；对这些系数进行正则化，反应特征的分量和重要程度。

sfm=SelectFromModel(estimator=DecisionTreeRegressor(),threshold=0.1)
sfm.fit_transform(X,Y)

此处estimator选择的是决策树回归器，也可以选择其它估算器，如LogisticRegression()
结果：（剔除了第二个特征）
array([[ 0.63265873,  0.15137685],
       [-0.81065328, -0.50542238],
       [ 0.43609265, -0.52941374],
       [ 1.15385088,  0.6536819 ],
       [ 1.5145949 , -0.35270394],
       [ 2.51115888,  1.61155123],
       [ 0.82370728, -1.04436562],
       [-1.96992943, -0.6010865 ],
       [ 0.20194085, -0.40571387],
       [ 0.33187617, -0.09669064]])

sfm=SelectFromModel(estimator=DecisionTreeRegressor(),threshold=1)
sfm.fit_transform(X,Y)

sfm=SelectFromModel(estimator=DecisionTreeRegressor(),threshold=0.00001)
sfm.fit_transform(X,Y)
#特征选择中采用样本进行特征筛选，而在正式建模中用全量数据。

需要根据实际需求设置合适的阈值threshold，否则特征筛选会失效

阈值太大，未保留特征：
array([], shape=(10, 0), dtype=float64)

阈值太小，使得保留了全部特征：
array([[-1.4947437 , 0.0191614 , 0.81820452], 
       [ 1.17189307, 1.87263454, -0.62936116],
       [ 1.66200794, 0.04248227, -0.93867893], 
       [ 1.05921792, 1.12342252, 0.44950437], 
       [-0.98050763, 0.20740876, -0.81644488], 
       [ 1.12914645, 0.06613361, -0.93451392], 
       [ 1.05055975, 0.08146466, -0.82193997],
       [ 1.73538698, -0.66855376, -0.41963065],
       [-0.06377718, 0.35172305, 1.02001796],
       [-1.51747269, -1.73222423, -0.10001505]])

2、特征变换

• 对指化（缩放尺度，单调性不变）

• 离散化（将连续变量分成几段bins）

#等频分箱
lst=[6,8,10,15,16,24,25,40,67]
pd.qcut(lst,q=3)
pd.qcut(lst,q=3,labels=["low","medium","high"])

#等距分箱
pd.cut(lst,bins=3)
pd.cut(lst,bins=3,labels=["low","medium","high"])

需要先排序

等频分箱：每个箱子的深度（数值的个数）一致

['low', 'low', 'low', 'medium', 'medium', 'medium', 'high', 'high', 'high']
Categories (3, object): ['low' < 'medium' < 'high']

等距分箱：每个箱子的宽度（数值的区间间距）一致

['low', 'low', 'low', 'low', 'low', 'low', 'low', 'medium', 'high']
Categories (3, object): ['low' < 'medium' < 'high']

• 归一化或标准化

from sklearn.preprocessing import MinMaxScaler,StandardScaler
#归一化
MinMaxScaler().fit_transform(np.array([1,4,10,15,21]).reshape(-1,1))
#标准化
X=np.array([1,0,0,0,0,0,0,0]).reshape(-1,1)

stand=StandardScaler().fit(X)
stand.transform(X)

#fit()+transform()==fit_transform()

StandardScaler().fit_transform(X)

归一化：（放缩到区间[0，1]）

array([[0.  ],
       [0.15],
       [0.45],
       [0.7 ],
       [1.  ]])

标准化：（数据满足标准正态分布，均值为0，方差为1）

array([[ 2.64575131],
       [-0.37796447],
       [-0.37796447],
       [-0.37796447],
       [-0.37796447],
       [-0.37796447],
       [-0.37796447],
       [-0.37796447]])

• 数值化

1. 数值标签化：赋予距离比较的含义0，1，2
2. 独热编码：无距离含义，仅表示类别

from sklearn.preprocessing import LabelEncoder,OneHotEncoder
#数值标签化
LabelEncoder().fit_transform(np.array(["Down","Up","Up","Down"]).reshape(-1,1))

LabelEncoder().fit_transform(np.array(["Low","Medium","High","Medium","Low"]).reshape(-1,1))

#独热编码
lb_encoder=LabelEncoder()
lb_train_f=lb_encoder.fit_transform(np.array(["Red","Yello","Green","Blue","Green"]))
print(lb_train_f)  #按照首字母顺序排序，先转化成标签
oht_encoder=OneHotEncoder().fit(lb_train_f.reshape(-1,1))
oht_encoder.transform(lb_train_f.reshape(-1,1))
oht_encoder.transform(lb_train_f.reshape(-1,1)).toarray()

1、按照开头字母的顺序进行排序，标签化：
array([0, 1, 1, 0], dtype=int64)
array([1, 2, 0, 2, 1], dtype=int64)

2、独热编码需要先转化成标签，再转化成稀疏矩阵：
[2 3 1 0 1]
array([[0., 0., 1., 0.],
       [0., 0., 0., 1.],
       [0., 1., 0., 0.],
       [1., 0., 0., 0.],
       [0., 1., 0., 0.]])

• 正规化（规范化）——可以反应特征对于标注的影响程度占比

1. 直接用在特征上
2. 用在每个对象的各个特征的表示（特征矩阵的行）
3. 模型的参数上（回归模型的使用较多）

from sklearn.preprocessing import Normalizer
#正规化（规范化）
Normalizer(norm="l1").fit_transform(np.array([[1,1,3,-1,2]]))  #正规化是行运算
Normalizer(norm="l2").fit_transform(np.array([[1,1,3,-1,2]]))

L1正则化：绝对值形式
array([[ 0.125,  0.125,  0.375, -0.125,  0.25 ]])

L2正则化：均方根形式
array([[ 0.25,  0.25,  0.75, -0.25,  0.5 ]])

特别注意：正则化为行运算，不能用reshape(-1,1)转换成列向量

3、特征降维

• PCA（无监督降维方法，无需用到标注）

1. 求特征协方差矩阵
2. 求协方差矩阵的特征值和特征向量
3. 将特征值按照从大到小的顺序排序，选择其中最大的k个
4. 将样本点投影到选取的特征向量上

• LDA（线性判别式分析Linear Discriminant Analysis）

核心思想：投影变化后同一标注内的距离尽可能小；不同标注间的距离尽可能大。

#1、特征降维LDA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
X=np.array([[-1,-1],[-2,-1],[-3,-2],[1,1],[2,1],[3,2]])
Y=np.array([1,1,1,2,2,2])
LinearDiscriminantAnalysis(n_components=1).fit_transform(X,Y)   #降到一维

#2、作为一个分类器使用：fisher classifier
clf=LinearDiscriminantAnalysis(n_components=1).fit(X,Y) 
clf.predict([[0.8,1]])

1、有监督的特征降维，降维后的特征量
array([[-1.73205081],
       [-1.73205081],
       [-3.46410162],
       [ 1.73205081],
       [ 1.73205081],
       [ 3.46410162]])

2、作为分类器的预测结果：（fisher分类器）
array([2])

4、特征衍生

• 四则运算（加减乘除）

• 求导或者高阶导数

• 人工归纳（从经验出发拓展特征维度）

三、具体HR的案例分析

整体特征工程的流程：

1、读入数据集

2、清洗数据集（异常值处理或抽样）

3、分离标注和特征

4、特征筛选（略）

5、特征处理：

数值型数据采用归一化或者标准化；

分类型数据采用标签化或者独热编码；

这里通过设置布尔值实现：

False——归一化；True——标准化；

False——标签化；True——独热编码；

6、特征降维（规定降维后的维度）

#HR表的特征预处理
import numpy as np
import pandas as pd

from sklearn.preprocessing import MinMaxScaler,StandardScaler  #归一化、标准化
from sklearn.preprocessing import LabelEncoder,OneHotEncoder  #数值化
from sklearn.preprocessing import Normalizer  #正规化
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis #特征降维
from sklearn.decomposition import PCA

#s1:satisfaction_level--False:MinMaxScaler;True:StandardScaler
#le:last_evaluation--False:MinMaxScaler;True:StandardScaler
#npr:number_project--False:MinMaxScaler;True:StandardScaler
#amh:average_montly_hours--False:MinMaxScaler;True:StandardScaler  
#tsc:time_spend_company--False:MinMaxScaler;True:StandardScaler  
#wa:Work_accident--False:MinMaxScaler;True:StandardScaler
#pl5:promotion_last_5years--False:MinMaxScaler;True:StandardScaler

#dp:Department--False:LabelEncoder;True:OneHotEncoder
#slr：salary--False:LabelEncoder;True:OneHotEncoder

#lower_d--False:不降维;True:降维,ld_n
def hr_preprocessing(sl = False,le=False,npr=False,amh=False,tsc=False,wa=False,\
                     pl5=False,dp=False,slr=False,lower_d=False,ld_n=1):
    df = pd.read_csv("d:/Users/Administrator/Desktop/python_code/HR_comma_sep.csv")
    
    #1.清洗数据（去除异常值或者抽样）
    df=df.dropna(subset=["satisfaction_level","last_evaluation"])
    df=df[df["satisfaction_level"] <= 1][df["salary"] != "nme"]
    
     #2.得到标注（最近是否有人离职,axis=1列）
    label=df["left"]
    df=df.drop("left",axis=1)
    #3.特征选择
    #4.特征处理
    
    #satisfaction_level处理方法(利用参数进行控制)：
    #(1)不处理
    #(2)强行拉伸到0~1之间 False
    #(3)数值型数据可以利用标准化方法 True
    scaler_lst=[sl,le,npr,amh,tsc,wa,pl5]#布尔型
    column_lst=["satisfaction_level","last_evaluation","number_project","average_montly_hours",\
                "time_spend_company","Work_accident","promotion_last_5years"]
    
    #第一个reshape是因为要求为列才可以处理，第二个是将数据变成行，
    #又因为它是二维数据，所以我们取[0]
    for i in range(len(scaler_lst)):
        if not scaler_lst[i]:
            df[column_lst[i]]=\
                MinMaxScaler().fit_transform(df[column_lst[i]].values.reshape(-1,1)).reshape(1,-1)[0]
        else:
            df[column_lst[i]]=\
                StandardScaler().fit_transform(df[column_lst[i]].values.reshape(-1,1)).reshape(1,-1)[0]
    
    #Department、salary都是类别离散值，需要先进行数值化
    scaler_lst=[slr,dp]
    column_lst=["department","salary"]
    
    #第一个reshape是因为要求为列才可以处理，第二个是将数据变成行，
    #又因为它是二维数据，所以我们取[0]
    for i in range(len(scaler_lst)):
        if not scaler_lst[i]:
            if column_lst[i] == "salary":
                df[column_lst[i]] = [map_salary(s) for s in df["salary"].values]
            else:
                df[column_lst[i]]=LabelEncoder().fit_transform(df[column_lst[i]])
            df[column_lst[i]]=MinMaxScaler().fit_transform(df[column_lst[i]].values.reshape(-1,1)).reshape(1,-1)[0]
        else:
            df=pd.get_dummies(df,columns=[column_lst[i]]) #独热编码OneHotEncoder
    
    #5.特征降维
    if lower_d:
        return PCA(n_components=ld_n).fit_transform(df.values)
    
    return df,label

#进行排序的时候，会令low=2，这里处理一下
d=dict([("low",0),("medium",1),("high",2)])
def map_salary(s):
    #找不到，就默认s=0
    return d.get(s,0)
###get()——函数返回指定键的值。
#在 key（键）不在字典中时，可以返回默认值 None 或者设置的默认值0。

def main():
    print(hr_preprocessing(lower_d=False,ld_n=3))
if __name__=='__main__':
    main()