Bootstrap

MUSIC算法详解

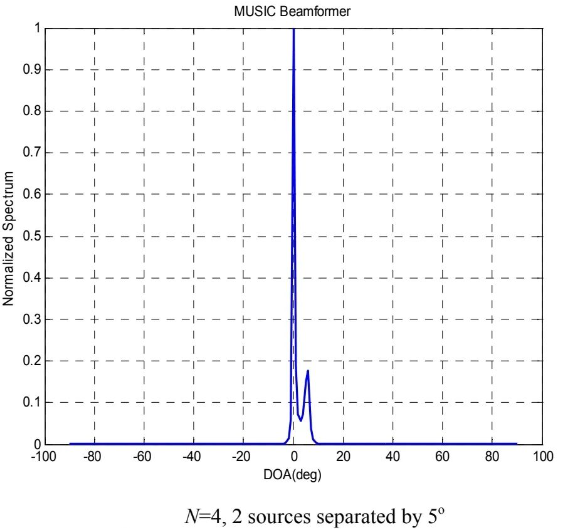
MUSIC (Multiple Signal Classification) 算法是一种基于子空间方法的高分辨率谱估计技术，广泛应用于信号处理领域，特别是在方向估计（如阵列信号处理中的到达角度（DOA）估计）中非常有效。它是由Schmidt于1986年提出的，用于估计从多个方向接收到的窄带信号的方向。MUSIC算法能够提供比传统波束形成技术更高的分辨率，特别适合于处理信号源个数少于接收传感器个数的情况。

MUSIC算法的核心思想是利用接收信号的协方差矩阵，将信号空间和噪声空间分离，进而利用它们的正交性质来估计信号的方向。

目录

 

MUSIC算法的基本原理和步骤

  1. 数据模型
    MUSIC算法考虑的是一个线性阵列接收到的来自多个远场点源的窄带信号。这些信号被假设为相互独立的，并且每个信号的波达方向（DOA，Direction of Arrival）是不同的。接收到的信号经过阵列处理后，可以得到一个接收信号矩阵。（假设有P个窄带远场信号从不同方向到达一个由N个传感器组成的阵列，P<N，这些信号在接收阵列处被叠加。每个信号可能具有不同的频率和相位。）

  2. 协方差矩阵估计
    首先，计算接收信号的协方差矩阵。这通常通过对接收信号矩阵进行时间平均来实现。协方差矩阵反映了接收到的信号之间的相关性。

  3. 特征分解
    将协方差矩阵进行特征值分解（或奇异值分解）。这一步骤将协方差矩阵分解为多个特征向量和特征值。特征向量对应于信号空间和噪声空间的方向，而特征值反映了各个方向上的能量大小。

在这里插入图片描述

  1. 信号空间和噪声空间
    根据特征值的大小，将特征向量划分为信号子空间和噪声子空间。信号子空间由对应于最大特征值的特征向量构成，噪声子空间则由其余的特征向量构成。理论上，信号子空间的维度等于信号源的数量。

在这里插入图片描述

  1. 方向估计
    利用噪声子空间构造一个空间谱函数。由于信号方向对应的波达方向与噪声子空间是正交的，空间谱函数在信号的DOA处会出现峰值。通过搜索这个空间谱函数的峰值，可以估计出信号的波达方向。

在这里插入图片描述
在这里插入图片描述
与经典波束成形器一样，您可以遍历所需的θ值并找到P的最大峰值，该峰值对应于您希望测量的到达角(参数θ)。

参考自：https://mp.weixin.qq.com/s/9XforfJUpzMQV1LQKIz7iQ

 

MUSIC算法特点

  • 高分辨率：MUSIC算法可以实现超过传统波束形成技术的分辨率，能够区分非常接近的信号源。
  • 要求信号源数量少于阵列元素数量：为了正确分离信号子空间和噪声子空间，信号源的数量必须小于接收阵列的元素数量。
  • 对模型参数敏感：MUSIC算法的性能依赖于对信号源数量的准确估计，以及阵列的校准。

MUSIC算法是一种强大的方向估计技术，适用于多种信号处理应用，如雷达、声纳和无线通信等领域。尽管它具有高分辨率的优点，但在实际应用中，对信号和阵列模型的要求也相对较高。

 

代码

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from matplotlib.animation import FuncAnimation

sample_rate = 1e6
N = 10000 # number of samples to simulate

# Create a tone to act as the transmitted signal
t = np.arange(N)/sample_rate
f_tone = 0.02e6
tx = np.exp(2j*np.pi*f_tone*t)

# Simulate three omnidirectional antennas in a line with 1/2 wavelength between adjancent ones, receiving a signal that arrives at an angle

d = 0.5
Nr = 3
theta_degrees = 20 # direction of arrival
theta = theta_degrees / 180 * np.pi # convert to radians
a = np.exp(-2j * np.pi * d * np.arange(Nr) * np.sin(theta))
print(a)

# we have to do a matrix multiplication of a and tx, so first lets convert both to matrix' instead of numpy arrays which dont let us do 1d matrix math
a = a.reshape(-1,1)
#print(a.shape) # 3x1
tx = tx.reshape(-1,1)
#print(tx.shape) # 10000x1

# so how do we use this? simple:

r = a.T @ tx  # matrix multiply. dont get too caught up by the transpose a, the important thing is we're multiplying the array factor by the tx signal
print(r.shape) # r is now going to be a 2D array, 1d is time and 1d is spatial

# Plot the real part of the first 200 samples of all three elements

fig, (ax1) = plt.subplots(1, 1, figsize=(7, 3))
ax1.plot(np.asarray(r[0,:]).squeeze().real[0:200]) # the asarray and squeeze are just annoyances we have to do because we came from a matrix
ax1.plot(np.asarray(r[1,:]).squeeze().real[0:200])
ax1.plot(np.asarray(r[2,:]).squeeze().real[0:200])
ax1.set_ylabel("Samples")
ax1.set_xlabel("Time")
ax1.grid()
ax1.legend(['0','1','2'], loc=1)
plt.show()

# note the phase shifts, they are also there on the imaginary portions of the samples

# So far this has been simulating the recieving of a signal from a certain angle of arrival
# in your typical DOA problem you are given samples and have to estimate the angle of arrival(s)
# there are also problems where you have multiple receives signals from different directions and one is the SOI while another might be a jammer or interferer you have to null out

# One thing we didnt both doing- lets add noise to this recieved signal.
# AWGN with a phase shift applied is still AWGN so we can add it after or before the array factor is applied, doesnt really matter, we'll do it after
# we need to make sure each element gets an independent noise signal added

n = np.random.randn(Nr, N) + 1j*np.random.randn(Nr, N)
r = r + 0.1*n


fig, (ax1) = plt.subplots(1, 1, figsize=(7, 3))
ax1.plot(np.asarray(r[0,:]).squeeze().real[0:200]) # the asarray and squeeze are just annoyances we have to do because we came from a matrix
ax1.plot(np.asarray(r[1,:]).squeeze().real[0:200])
ax1.plot(np.asarray(r[2,:]).squeeze().real[0:200])
ax1.set_ylabel("Samples")
ax1.set_xlabel("Time")
ax1.grid()
ax1.legend(['0','1','2'], loc=1)
plt.show()


# MUSIC with complex scenario
if False:
    # more complex scenario
    Nr = 8 # 8 elements
    theta1 = 20 / 180 * np.pi # convert to radians
    theta2 = 25 / 180 * np.pi
    theta3 = -40 / 180 * np.pi
    a1 = np.exp(-2j * np.pi * d * np.arange(Nr) * np.sin(theta1)).reshape(-1,1) # 8x1
    a2 = np.exp(-2j * np.pi * d * np.arange(Nr) * np.sin(theta2)).reshape(-1,1)
    a3 = np.exp(-2j * np.pi * d * np.arange(Nr) * np.sin(theta3)).reshape(-1,1)
    # we'll use 3 different frequencies.  1xN
    tone1 = np.exp(2j*np.pi*0.01e6*t).reshape(1,-1)
    tone2 = np.exp(2j*np.pi*0.02e6*t).reshape(1,-1)
    tone3 = np.exp(2j*np.pi*0.03e6*t).reshape(1,-1)
    r = a1 @ tone1 + a2 @ tone2 + 0.1 * a3 @ tone3
    n = np.random.randn(Nr, N) + 1j*np.random.randn(Nr, N)
    r = r + 0.05*n # 8xN

    # MUSIC Algorithm (part that doesn't change with theta_i)
    num_expected_signals = 3 # Try changing this!
    R = r @ r.conj().T # Calc covariance matrix, it's Nr x Nr
    w, v = np.linalg.eig(R) # eigenvalue decomposition, v[:,i] is the eigenvector corresponding to the eigenvalue w[i]

    if False:
        fig, (ax1) = plt.subplots(1, 1, figsize=(7, 3))
        ax1.plot(10*np.log10(np.abs(w)),'.-')
        ax1.set_xlabel('Index')
        ax1.set_ylabel('Eigenvalue [dB]')
        plt.show()
        #fig.savefig('../_images/doa_eigenvalues.svg', bbox_inches='tight') # I EDITED THIS ONE IN INKSCAPE!!!
        exit()

    eig_val_order = np.argsort(np.abs(w)) # find order of magnitude of eigenvalues
    v = v[:, eig_val_order] # sort eigenvectors using this order
    V = np.zeros((Nr, Nr - num_expected_signals), dtype=np.complex64) # Noise subspace is the rest of the eigenvalues
    for i in range(Nr - num_expected_signals):
        V[:, i] = v[:, i]

    theta_scan = np.linspace(-1*np.pi, np.pi, 1000) # 100 different thetas between -180 and +180 degrees
    results = []
    for theta_i in theta_scan:
        a = np.exp(-2j * np.pi * d * np.arange(Nr) * np.sin(theta_i))
        a = a.reshape(-1,1)
        metric = 1 / (a.conj().T @ V @ V.conj().T @ a) # The main MUSIC equation
        metric = np.abs(metric.squeeze()) # take magnitude
        metric = 10*np.log10(metric) # convert to dB
        results.append(metric)
    results -= np.max(results) # normalize

    fig, ax = plt.subplots(subplot_kw={'projection': 'polar'})
    ax.plot(theta_scan, results) # MAKE SURE TO USE RADIAN FOR POLAR
    ax.set_theta_zero_location('N') # make 0 degrees point up
    ax.set_theta_direction(-1) # increase clockwise
    ax.set_rlabel_position(30)  # Move grid labels away from other labels
    plt.show()
    fig.savefig('../_images/doa_music.svg', bbox_inches='tight')
    exit()


# MUSIC animation changing angle of two
if False:
    Nr = 8 # 8 elements
    num_expected_signals = 2

    theta2s = np.arange(15,21,0.05) / 180 * np.pi
    theta_scan = np.linspace(-1*np.pi, np.pi, 2000)
    results = np.zeros((len(theta2s), len(theta_scan)))
    for theta2s_i in range(len(theta2s)):
        theta1 = 18 / 180 * np.pi # convert to radians
        theta2 = theta2s[theta2s_i]
        a1 = np.exp(-2j * np.pi * d * np.arange(Nr) * np.sin(theta1))
        a1 = a1.reshape(-1,1)
        a2 = np.exp(-2j * np.pi * d * np.arange(Nr) * np.sin(theta2))
        a2 = a2.reshape(-1,1)
        tone1 = np.exp(2j*np.pi*0.01e6*t)
        tone1 = tone1.reshape(-1,1)
        tone2 = np.exp(2j*np.pi*0.02e6*t)
        tone2 = tone2.reshape(-1,1)
        r = a1 @ tone1.T + a2 @ tone2.T
        n = np.random.randn(Nr, N) + 1j*np.random.randn(Nr, N)
        r = r + 0.01*n
        R = r @ r.conj().T # Calc covariance matrix, it's Nr x Nr
        w, v = np.linalg.eig(R) # eigenvalue decomposition, v[:,i] is the eigenvector corresponding to the eigenvalue w[i]
        eig_val_order = np.argsort(np.abs(w)) # find order of magnitude of eigenvalues
        v = v[:, eig_val_order] # sort eigenvectors using this order
        V = np.zeros((Nr, Nr - num_expected_signals), dtype=np.complex64) # Noise subspace is the rest of the eigenvalues
        for i in range(Nr - num_expected_signals):
            V[:, i] = v[:, i]
        for theta_i in range(len(theta_scan)):
            a = np.exp(-2j * np.pi * d * np.arange(Nr) * np.sin(theta_scan[theta_i]))
            a = a.reshape(-1,1)
            metric = 1 / (a.conj().T @ V @ V.conj().T @ a) # The main MUSIC equation
            metric = np.abs(metric.squeeze()) # take magnitude
            metric = 10*np.log10(metric) # convert to dB
            results[theta2s_i, theta_i] = metric

        results[theta2s_i,:] /= np.max(results[theta2s_i,:]) # normalize

    fig, ax = plt.subplots(subplot_kw={'projection': 'polar'})
    fig.set_tight_layout(True)
    line, = ax.plot(theta_scan, results[0,:])
    ax.set_thetamin(0)
    ax.set_thetamax(30) 
    ax.set_theta_zero_location('N') # make 0 degrees point up
    ax.set_theta_direction(-1) # increase clockwise
    ax.set_rlabel_position(22.5)  # Move grid labels away from other labels
    def update(i):
        i = int(i)
        print(i)
        results_i = results[i,:] #/ np.max(results[i,:]) * 10 # had to add this in for the last animation because it got too large
        line.set_ydata(results_i)
        return line, ax
    anim = FuncAnimation(fig, update, frames=np.arange(0, len(theta2s)), interval=100)
    anim.save('../_images/doa_music_animation.gif', dpi=80, writer='imagemagick')
    exit()

参考自：https://github.com/777arc/PySDR/blob/master/figure-generating-scripts/doa.py

 

Smooth-MUSIC

Smooth MUSIC算法是MUSIC算法的一种变体，主要用于提高小型阵列或者当信号源数接近阵列元素数时的性能。该方法通过对接收到的信号数据矩阵进行平滑处理来增加虚拟的阵列元素，从而增强算法的分辨能力。

工作原理:

  • 数据平滑：Smooth-MUSIC通过对接收到的信号矩阵进行滑动平均或其他平滑技术处理，构造出一个“扩展”的数据矩阵。这种处理仿佛在物理上增加了阵列接收元素的数量，有助于提高算法的分辨率。
  • 子空间分解：与传统MUSIC算法类似，Smooth-MUSIC也采用特征值分解（EVD）或奇异值分解（SVD）来从扩展的数据矩阵中分离出信号子空间和噪声子空间。
  • 谱峰搜索：通过构建一个基于信号子空间和噪声子空间正交性的谱函数，并在感兴趣的方向范围内搜索该函数的峰值，从而估计信号源的方向。

优点

  • 提高分辨率：对于小阵列或信号源数接近阵列元素数的情况，Smooth-MUSIC能够提供比传统MUSIC更高的分辨率。
  • 强化性能：平滑处理有助于减少估计方向时的方差，使得算法在低信噪比条件下也能保持较好的性能。

缺点

  • 复杂度增加：平滑处理增加了计算复杂度，尤其是在处理大规模数据时。
  • 设计选择：平滑窗口的大小和类型需要根据具体情况仔细选择，以平衡性能和复杂度。

 

Cyclic-MUSIC

Cyclic-MUSIC是MUSIC算法的另一种变体，专门设计用于处理具有周期性的信号。这种方法利用信号的周期性特性来提高频域信号源的定位精度。

工作原理

  • 周期性信号分析：Cyclic-MUSIC算法利用信号的周期性统计特性来进行信号源定位。通过分析接收信号的循环谱，可以提取出信号的周期性特征，这对于某些特定类型的信号（如通信信号）非常有用。
  • 子空间分解：与传统MUSIC算法一样，Cyclic-MUSIC也使用子空间方法。不同之处在于，它在循环谱域内进行操作，根据信号的循环频率来区分信号子空间和噪声子空间。
  • DOA估计：通过构造基于循环谱的谱峰搜索函数，Cyclic-MUSIC可以精确估计具有周期性特征的信号源方向。

 

其他MUSIC变体

  • Root-MUSIC：适用于等间距线性阵列，通过求解特定多项式的根来直接估计信号方向。这种方法可以降低计算复杂度，提高计算速度。

  • ESPRIT：利用阵列元素间的转动不变性，无需进行多维搜索即可估计信号源的方向。ESPRIT算法在计算效率上通常优于传统MUSIC，但需要特定的阵列几何结构。

  • Min-Norm：这种方法通过最小化一个基于噪声子空间的投影算子的范数来估计信号方向。它特别适用于信号源数量较少时的场景。

  • 2D-MUSIC & 3D-MUSIC：针对二维空间和三维空间信号源定位问题的MUSIC算法扩展。这些方法能够估计信号源的方位角和俯仰角，适用于更复杂的空间信号处理任务。

  • Focused-MUSIC：针对具有高分辨率需求的应用进行了优化。通过在感兴趣的区域内集中处理能力，可以更加精确地估计那些区域内的信号源方向。

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
从Apple Intelligence到远程机器人手术：更快、更安全的网络成企业业务关键
收银系统源码
Windows环境下安装及部署Nginx
Java中有关锁的面试题
结合无监督表示学习与伪标签监督的自蒸馏方法，用于稀有疾病影像表型分类的分散感知失衡校正|文献速递-基于生成模型的数据增强与疾病监测应用
matlab矩量法求解八木天线（五元）传输模型积分方程
随笔一、泰山派RK3566开发板调试串口波特率修改
Android fragment控制activity中的控件
CyberVadis评估！
比teamviewer更屌的远程软件，程序员莫错过
;