图的遍历

前置知识点：图的基本概念、4种存储结构、基本操作详解

图的遍历是指从图中的某一顶点出发，按照某种搜索方法沿着图中的边对图中的所有顶点访问一次且仅访问一次。注意到树是一种特殊的图，所以树的遍历实际上也可视为一种特殊的图的遍历。图的遍历算法是求解图的连通性问题、拓扑排序和求关键路径等算法的基础。

图的遍历比树的遍历要复杂得多，因为图的任一顶点都可能和其余的顶点相邻接，所以在访问某个顶点后，可能沿着某条路径搜索又回到该顶点上。为避免同一顶点被访问多次，在遍历图的过程中，必须记下每个已访问过的顶点，为此可以设一个辅助数组visited[]来标记顶点是否被访问过。图的遍历算法主要有两种：广度优先搜索和深度优先搜索。

深度优先搜索

1.用DFS遍历图

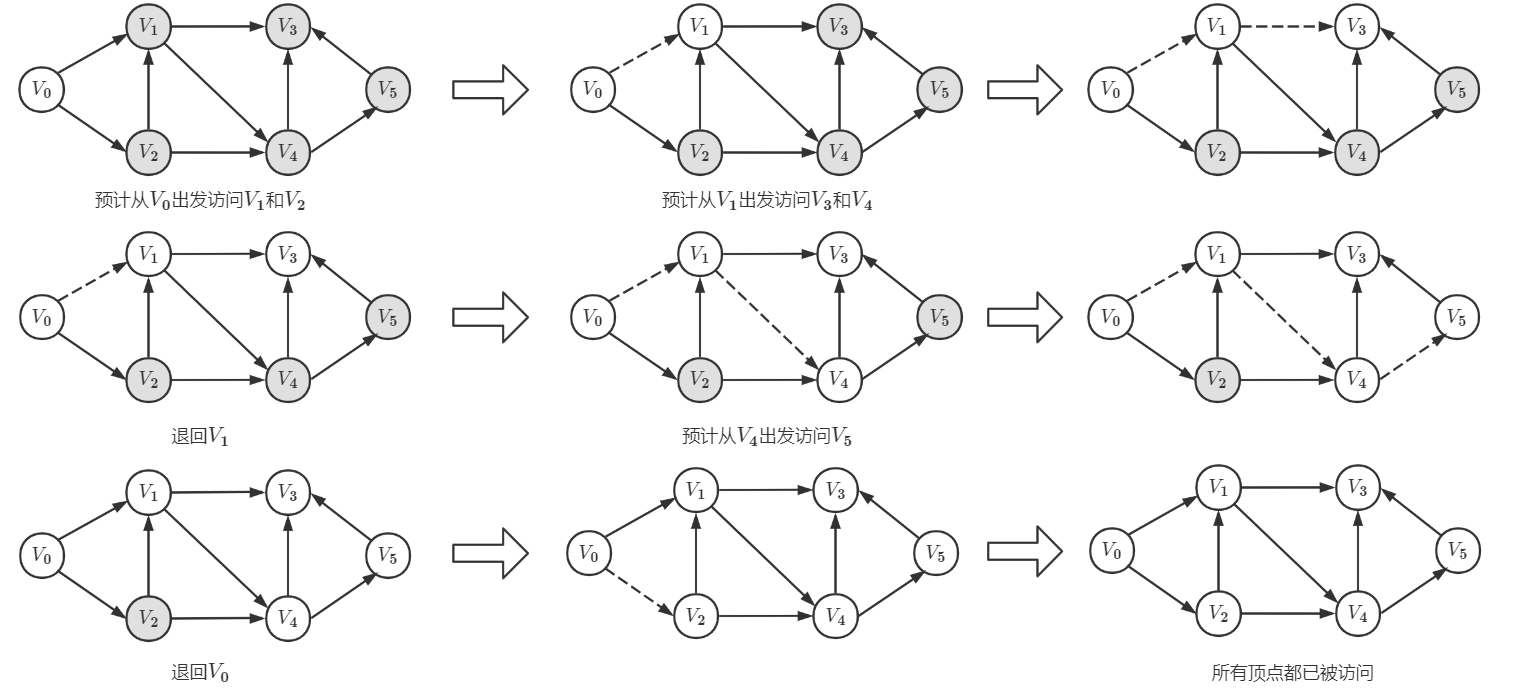
深度优先搜索以“深度”作为第一关键词，每次都是沿着路径到不能再前进时才退回到最近的岔道口。以一个有向图（见下图）进行 $\mathrm{DFS}$ 遍历来举例（从 ${\mathrm{V}}_0$ 开始进行遍历，黑色表示结点未访问，白色表示结点已访问，虚线边表示当前遍历路径）：

1）访问 ${\mathrm{V}}_0$ ，发现从 ${\mathrm{V}}_0$ 出发可以到达两个未访问顶点： ${\mathrm{V}}_1$ 和 ${\mathrm{V}}_2$ ，因此准备访问 ${\mathrm{V}}_1$ 和 ${\mathrm{V}}_2$ 这两个顶点。
2）从 ${\mathrm{V}}_0$ 出发访问 ${\mathrm{V}}_1$ ，发现从 ${\mathrm{V}}_1$ 出发可以到达两个未访问顶点： ${\mathrm{V}}_3$ 和 ${\mathrm{V}}_4$ ，因此准备访问 ${\mathrm{V}}_3$ 和 ${\mathrm{V}}_4$ 这两个顶点。
3）从 ${\mathrm{V}}_1$ 出发访问 ${\mathrm{V}}_3$ ，但是从 ${\mathrm{V}}_3$ 出发不能到达任何未访问顶点，因此退回到当前路径上距离 ${\mathrm{V}}_3$ 最近的仍有未访问分支顶点的岔道口 ${\mathrm{V}}_1$ 。
4）从 ${\mathrm{V}}_1$ 出发访问 ${\mathrm{V}}_4$ ，发现从 ${\mathrm{V}}_4$ 出发可以到达一个未访问顶点： ${\mathrm{V}}_5$ ，因此准备前往访问 ${\mathrm{V}}_5$ 。
5）从 ${\mathrm{V}}_4$ 出发访问 ${\mathrm{V}}_5$ ，发现从 ${\mathrm{V}}_5$ 出发不能到达任何未访问顶点，因此退回到当前路径上距离 ${\mathrm{V}}_5$ 最近的仍有未访问分支顶点的岔道口 ${\mathrm{V}}_0$ 。
6）从 ${\mathrm{V}}_0$ 出发访问 ${\mathrm{V}}_2$ ，发现从 ${\mathrm{V}}_2$ 出发不能到达任何未访问顶点，因此退回到当前路径上距离 ${\mathrm{V}}_2$ 最近的仍有未访问分支顶点的岔道口。但是此时路径上所有顶点的分支顶点都已被访问，因此 $\mathrm{DFS}$ 算法结束。

总而言之，使用 $\mathrm{DFS}$ 来遍历图就跟上面的例子那样，沿着一条路径直到无法继续前进，才退回到路径上离当前顶点最近的还存在未访问分支顶点的岔道口，并前往访问那些未访问分支顶点，直到遍历完整个图。

2.DFS的具体实现

可以想象，如果要遍历整个图，就需要对所有连通块（连通分量和强连通分量）分别进行遍历。所以 $\mathrm{DFS}$ 遍历图的基本思路就是将经过的顶点设置为已访问，在下次递归碰到这个顶点时就不再去处理，直到整个图的顶点都被标记为已访问。

下面是一份 $\mathrm{DFS}$ 的伪代码，不管是使用邻接矩阵还是邻接表，都是使用这种思想。注意：如果已知给定的图是一个连通图，则只需要一次 $\mathrm{DFS}$ 就能完成遍历。

DFS(u){ //访问顶点u
    vis[u] = true;  //设置u已被访问
    for (从u出发能到达的所有顶点v) //枚举从u出发可以到达的所有顶点v
        if vis[v]== false //如果v未被访问
            DFS(v); //递归访问v
}

DFSTrave(G){  //遍历图G
    for (G的所有顶点u)   //对G的所有顶点u
        if vis[u]==false  //如果u未被访问
            DFS(u); //访问u所在的连通块
}

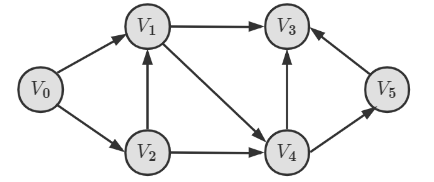
以一个有向图（见下图）进行 $\mathrm{DFS}$ 遍历来举例：

邻接矩阵版 $\mathrm{DFS}$ ：

#include <iostream>

using namespace std;

#define MaxVertexNum 100 //顶点数目的最大值

// VertexType，顶点的数据类型
template<typename VertexType>
class MGraph {
private:
    VertexType Vex[MaxVertexNum];   //顶点表
    int Edge[MaxVertexNum][MaxVertexNum];  //邻接矩阵，边表
    int vexnum, arcnum;  //图的当前顶点数和弧数
    bool visited[MaxVertexNum]; //如果顶点i已被访问,则visited[i]==true。初值为false

    void DFS(int u) {   //u为当前访问的顶点索引
        cout << Vex[u] << "\t";
        visited[u] = true;   //设置u已被访问
        for (int i = 0; i < vexnum; i++)
            if (Edge[u][i] == 1 && visited[i] == false)
                DFS(i);
    }

public:
    MGraph() {
        for (int i = 0; i < MaxVertexNum; i++) {
            visited[i] = false;
            for (int k = 0; k < MaxVertexNum; k++)
                Edge[i][k] = 0;
        }
    }

    void create() {
        int row, col;
        cin >> vexnum >> arcnum;    //输入实际图的顶点数和边数
        for (int i = 0; i < vexnum; i++)   //输入顶点信息
            cin >> Vex[i];

        for (int i = 0; i < arcnum; i++) {  //输入边信息
            cin >> row >> col;
            Edge[row][col] = 1;
        }
    }

    void DFSTrave() {  //遍历图G
        for (int u = 0; u < vexnum; u++)  //对每个顶点u
            if (visited[u] == false)  //如果u未被访问
                DFS(u); //访问u和u所在的连通块
    }
};

int main() {
    MGraph<string> G;
    G.create();
    G.DFSTrave();
    return 0;
}

输入数据：

6 9
v0 v1 v2 v3 v4 v5
0 1
0 2
1 3
1 4
2 1
2 4
4 3
4 5
5 3

输出结果：

v0      v1      v3      v4      v5      v2

邻接表版 $\mathrm{DFS}$ ：

#include <iostream>

using namespace std;

#define MaxVertexNum 100 //顶点数目的最大值

struct ArcNode {    //边表结点
    int adjvex;     //该弧所指向的顶点的位置
    ArcNode *next;  //指向下一条弧的指针
};

template<typename VertexType>
struct VNode {        //顶点表结点
    VertexType data;  //顶点信息
    ArcNode *first;   //指向第一条依附该顶点的弧的指针
};

template<typename VertexType>
class ALGraph { //ALGraph是以邻接表存储的图类型
private:
    VNode<VertexType> vertices[MaxVertexNum]; //邻接表
    int vexnum, arcnum; //图的顶点数和弧数
    bool visited[MaxVertexNum]; //如果顶点i已被访问,则visited[i]==true。初值为false

    void DFS(int u) {   //u为当前访问的顶点索引
        cout << vertices[u].data << "\t";
        visited[u] = true;   //设置u已被访问
        ArcNode *p = vertices[u].first;

        while (p) {
            if (visited[p->adjvex] == false)
                DFS(p->adjvex);
            p = p->next;
        }
    }

public:
    ALGraph() {
        for (int i = 0; i < MaxVertexNum; i++) {
            visited[i] = false;
            vertices[i].first = NULL;
        }
    }

    void create() {
        int row, col;
        cin >> vexnum >> arcnum;    //输入实际图的顶点数和边数
        for (int i = 0; i < vexnum; i++)   //输入顶点信息
            cin >> vertices[i].data;

        for (int i = 0; i < arcnum; i++) {  //输入边信息
            cin >> row >> col;
            ArcNode *p = new ArcNode;
            p->adjvex = col;
            p->next = vertices[row].first;
            vertices[row].first = p;
        }
    }

    void DFSTrave() {  //遍历图G
        for (int u = 0; u < vexnum; u++)  //对每个顶点u
            if (visited[u] == false)  //如果u未被访问
                DFS(u); //访问u和u所在的连通块
    }
};

int main() {
    ALGraph<string> G;
    G.create();
    G.DFSTrave();
    return 0;
}

输入数据：

6 9
v0 v1 v2 v3 v4 v5
0 1
0 2
1 3
1 4
2 1
2 4
4 3
4 5
5 3

输出结果：

v0      v2      v4      v5      v3      v1

广度优先搜索

广度优先搜索（ $\mathrm{Breadth}-\mathrm{First}-\mathrm{Search},\mathrm{BFS}$ ）类似于二叉树的层序遍历算法。基本思想是：首先访问起始顶点 $\mathrm{v}$ ，接着由 $\mathrm{v}$ 出发，依次访问 $\mathrm{v}$ 的各个未访问过的邻接顶点 ${\mathrm{w}}_{\mathrm{i}},{\mathrm{w}}_2,\dots ,{\mathrm{w}}_{\mathrm{i}}$ ，然后依次访问 ${\mathrm{w}}_{\mathrm{i}},{\mathrm{w}}_2,\dots ,{\mathrm{w}}_{\mathrm{i}}$ 的所有未被访问过的邻接顶点；再从这些访问过的顶点出发，访问它们所有未被访问过的邻接顶点，直至图中所有顶点都被访问过为止。若此时图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作为始点，重复上述过程，直至图中所有顶点都被访问到为止。 $\mathrm{Dijkstra}$ 单源最短路径算法和 $\mathrm{Prim}$ 最小生成树算法也应用了类似的思想。

换句话说，广度优先搜索遍历图的过程是以 $\mathrm{v}$ 为起始点，由近至远依次访问和 $\mathrm{v}$ 有路径相通且路径长度为1, 2, … 的顶点。广度优先搜索是一种分层的查找过程，每向前走一步可能访问一批顶点，不像深度优先搜索那样有往回退的情况，因此它不是一个递归的算法。为了实现逐层的访问，算法必须借助一个辅助队列，以记忆正在访问的顶点的下一层顶点。

1.用BFS遍历图

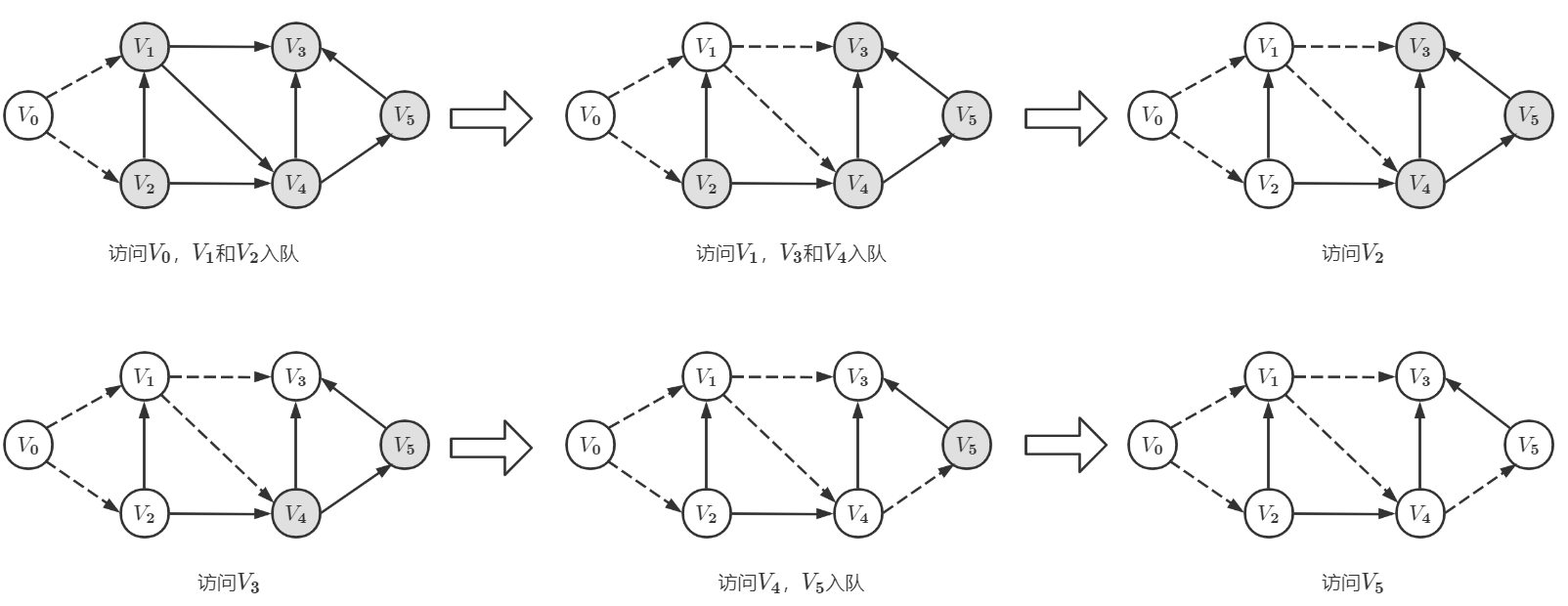
下面以一个有向图（见下图）作为 $\mathrm{BFS}$ 遍历的举例（初始时先将 ${\mathrm{V}}_0$ 加入队列，黑色表示结点未访问，白色表示结点已访问，虚线边表示当前遍历路径）：

1）当前队列内元素为 { V 0 } {\rm \{ V_0 \}} {V0​} ，取出队首元素 ${\mathrm{V}}_0$ 进行访问。之后，将从 ${\mathrm{V}}_0$ 出发能够到达的两个未曾加入过队列的顶点 ${\mathrm{V}}_1$、${\mathrm{V}}_2$ 加入队列。
2）当前队列内元素为 { V 1 , V 2 } {\rm \{ V_1,V_2 \}} {V1​,V2​} ，取出队首元素 ${\mathrm{V}}_1$ 进行访问。之后，将从 ${\mathrm{V}}_1$ 出发能够到达的两个未曾加入过队列的顶点 ${\mathrm{V}}_3$、${\mathrm{V}}_4$ 加入队列。
3）当前队列内元素为 { V 2 , V 3 , V 4 } {\rm \{ V_2,V_3,V_4 \}} {V2​,V3​,V4​} ，取出队首元素 ${\mathrm{V}}_2$ 进行访问。由于从 ${\mathrm{V}}_2$ 出发无法找到未曾加入过队列的顶点( ${\mathrm{V}}_1$、${\mathrm{V}}_4$ 均已加入过队列)，因此不予处理。
4）当前队列内元素为 { V 3 , V 4 } {\rm \{ V_3,V_4 \}} {V3​,V4​} ，取出队首元素 ${\mathrm{V}}_3$ 进行访问。由于从 ${\mathrm{V}}_3$ 出发无法找到未曾加入过队列的顶点，因此不予处理。
5）当前队列内元素为 { V 4 } {\rm \{ V_4 \}} {V4​} ，取出队首元素 ${\mathrm{V}}_4$ 进行访问。之后，将从 ${\mathrm{V}}_4$ 出发能够到达的一个未曾加入过队列的顶点 ${\mathrm{V}}_5$ 加入队列。
6）当前队列内元素为 { V 5 } {\rm \{ V_5 \}} {V5​} ，取出队首元素 ${\mathrm{V}}_5$ 进行访问。由于从 ${\mathrm{V}}_5$ 出发无法找到未曾加入过队列的顶点，因此不予处理。
7）当前队列为空， $\mathrm{BFS}$ 遍历结束。

2.BFS的具体实现

和 $\mathrm{DFS}$ 一样，上面的例子是对单个连通块进行的遍历操作。如果要遍历整个图，则需要对所有连通块分别进行遍历。使用 $\mathrm{BFS}$ 遍历图的基本思想是建立一个队列，并把初始顶点加入队列，此后每次都取出队首顶点进行访问，并把从该顶点出发可以到达的未曾加入过队列(而不是未访问）的顶点全部加入队列，直到队列为空。

下面给出 $\mathrm{BFS}$ 的伪代码：

BFS(u){ //遍历u所在的连通块
    queue q;    //定义队列q
    将u入队;
    inq[u] = true;  //设置u已被加入过队列
    while (q非空){   //只要队列非空
        取出q的队首元素u进行访问;
        for (从u出发可达的所有顶点v)     //枚举从u能直接到达的顶点v
            if (inq[v] == false) {   //如果v未曾加入过队列
                将v入队;
                inq[v] = true; //设置v已被加入过队列
            }
    }
}

BFSTrave(){ //遍历图G
    for (G的所有顶点u)   //枚举G的所有顶点u
        if (inq[u] == false)   //如果u未曾加入过队列
            BFS(u); //遍历u所在的连通块
}

下面分别使用邻接矩阵和邻接表实现 $\mathrm{BFS}$ 遍历图。

以一个有向图（见下图）进行 $\mathrm{BFS}$ 遍历来举例：

邻接矩阵版 $\mathrm{BFS}$ ：

#include <iostream>
#include <queue>

using namespace std;

#define MaxVertexNum 100 //顶点数目的最大值

// VertexType，顶点的数据类型
template<typename VertexType>
class MGraph {
private:
    VertexType Vex[MaxVertexNum];   //顶点表
    int Edge[MaxVertexNum][MaxVertexNum];  //邻接矩阵，边表
    int vexnum, arcnum;  //图的当前顶点数和弧数
    bool inq[MaxVertexNum]; //如果顶点i已入过,inq[i]==true。初值为false

    void BFS(int u) {   //遍历u所在的连通块
        queue<int> q;   //定义队列q
        q.push(u);   //初始顶点u入队
        inq[u] = true;  //设置u已入过队
        while (!q.empty()) {    //只要队列非空
            u = q.front();  //取出队首元素并访问
            cout << Vex[u] << "\t";
            q.pop();    //队首元素出队
            for (int v = 0; v < vexnum; v++)
                //如果u的邻接点v未曾加入过队列
                if (Edge[u][v] == 1 && inq[v] == false) {
                    //将v入队并标记已入队
                    q.push(v);
                    inq[v] = true;
                }
        }
    }

public:
    MGraph() {
        for (int i = 0; i < MaxVertexNum; i++) {
            inq[i] = false;
            for (int k = 0; k < MaxVertexNum; k++)
                Edge[i][k] = 0;
        }
    }

    void create() {
        int row, col;
        cin >> vexnum >> arcnum;    //输入实际图的顶点数和边数
        for (int i = 0; i < vexnum; i++)   //输入顶点信息
            cin >> Vex[i];

        for (int i = 0; i < arcnum; i++) {  //输入边信息
            cin >> row >> col;
            Edge[row][col] = 1;
        }
    }

    void BFSTrave() {  //遍历图G
        for (int u = 0; u < vexnum; u++) //枚举所有顶点
            if (inq[u] == false)
                BFS(u); //遍历u所在的连通块
    }
};

int main() {
    MGraph<string> G;
    G.create();
    G.BFSTrave();
    return 0;
}

输入数据：

6 9
v0 v1 v2 v3 v4 v5
0 1
0 2
1 3
1 4
2 1
2 4
4 3
4 5
5 3

输出结果：

v0      v1      v2      v3      v4      v5

邻接表版 $\mathrm{BFS}$ ：

#include <iostream>
#include <queue>

using namespace std;

#define MaxVertexNum 100 //顶点数目的最大值

struct ArcNode {    //边表结点
    int adjvex;     //该弧所指向的顶点的位置
    ArcNode *next;  //指向下一条弧的指针
};

template<typename VertexType>
struct VNode {        //顶点表结点
    VertexType data;  //顶点信息
    ArcNode *first;   //指向第一条依附该顶点的弧的指针
};

template<typename VertexType>
class ALGraph { //ALGraph是以邻接表存储的图类型
private:
    VNode<VertexType> vertices[MaxVertexNum]; //邻接表
    int vexnum, arcnum; //图的顶点数和弧数
    bool inq[MaxVertexNum]; //如果顶点i已入过,inq[i]==true。初值为false

    void BFS(int u) {   //遍历u所在的连通块
        queue<int> q;   //定义队列q
        q.push(u);   	//初始顶点u入队
        inq[u] = true;  //设置u已入过队
        while (!q.empty()) {
            u = q.front();  //取出队首元素并访问
            cout << vertices[u].data << "\t";
            q.pop();    //队首元素出队
            ArcNode *p = vertices[u].first;
            while (p) {
                if (inq[p->adjvex] == false) {
                    q.push(p->adjvex);
                    inq[p->adjvex] = true;
                }
                p = p->next;
            }
        }
    }

public:
    ALGraph() {
        for (int i = 0; i < MaxVertexNum; i++) {
            inq[i] = false;
            vertices[i].first = NULL;
        }
    }

    void create() {
        int row, col;
        cin >> vexnum >> arcnum;    //输入实际图的顶点数和边数
        for (int i = 0; i < vexnum; i++)   //输入顶点信息
            cin >> vertices[i].data;

        for (int i = 0; i < arcnum; i++) {  //输入边信息
            cin >> row >> col;
            ArcNode *p = new ArcNode;
            p->adjvex = col;
            p->next = vertices[row].first;
            vertices[row].first = p;
        }
    }

    void BFSTrave() {  //遍历图G
        for (int u = 0; u < vexnum; u++) //枚举所有顶点
            if (inq[u] == false)
                BFS(u); //遍历u所在的连通块
    }
};

int main() {
    ALGraph<string> G;
    G.create();
    G.BFSTrave();
    return 0;
}

输入数据：

6 9
v0 v1 v2 v3 v4 v5
0 1
0 2
1 3
1 4
2 1
2 4
4 3
4 5
5 3

输出结果：

v0      v2      v1      v4      v3      v5