仍没有进展，耐心读论文！

这次总结两篇文章去中心化的联邦学习

1. Hu, Y., Xia, W., Xiao, J., and Wu, C., “GFL: A Decentralized Federated Learning Framework Based On Blockchain”, arXiv e-prints, 2020.
2. Li C , Li G , Varshney P K . Decentralized Federated Learning via Mutual Knowledge Transfer[J]. 2020.

为什么要提出去中心化的联邦学习模型？

1. 当客户端特别多的时候，服务器发生故障的话，全局就瘫痪了。（鲁棒性，承受能力）
2. 模型太大，参数过多导致带宽压力太大，速度变慢，影响收敛。
3. 内部攻击，恶意节点冒充。（安全性）

   第一篇可以运行他的代码，非常开心。GFL: Galaxy Federated Learning

GFL 包括什么？

1. 区块链、IPFS（我认为类似hash,将大块数据压缩成46字节代替）-----存储、攻击
2. Ring-allreduce 环约减算法----去中心、节省带宽
3. 知识蒸馏----节省带宽和non-iid

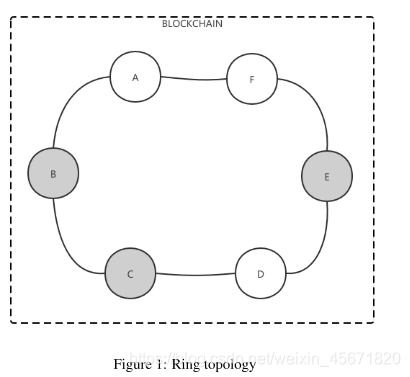
环

A,F,D 是诚实节点，B,C,E 是不诚实节点 。

（1）假设每一个节点同时完成本地训练，并使用IPFS对对应的文件进行操作。A,B,C,D,E,F 参数分别为 MA, MB , MC , MD, ME , MF .

      依据一致性hash算法，各个节点要将参数传输到可信节点上，如果可信节点宕机了，就会寻找最近的诚实节点。
     （不诚实节点——————>诚实节点）(减少了节点数)

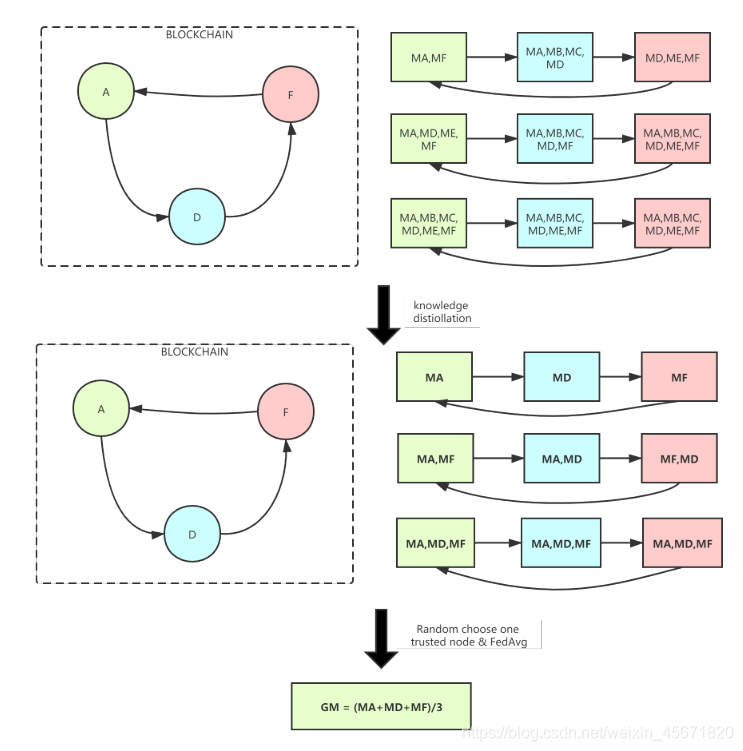
下面是参数的转移过程：

上述3轮过程，一次移动一步

1. 第一轮：MA ->B, B的参数有MA,MB, MB->C, C的参数有MB,MC，… 以此类推 ， F有 ME,MF ， A有 MA,MF 。
2. 第二轮：A的参数MA,MF移动到B ，B有MA,MB,MF, …以此类推，F有MD,ME,MF，A有 MA,MF,MD,ME
3. 第三轮： 六个节点都有MA,MB,MC,MD,ME,MF，达到稳定态，开始蒸馏。。

这里引入知识蒸馏技术和环约减技术，将可信节点的参数做平均，缩减了参数。

$$L_{student}=L_{CE}+D_{KL}(p_{teacher}||p_{student})$$

$L_{CE}$ 是交叉熵， $D_{KL}$是散度. $p_{teacher}$和$p_{student}$表示激活函数后输出的模型。

$$p_{teacher}=\frac{e^{z/T}}{{\sum }_{i}exp(z_i/T)}$$

T是蒸馏的温度, z是逻辑输出，此处用欧几里得距离代替散度去测量模型之间的分布差异。

$$L_{student}=L_{CE}+D_{ED}(z_{teacher}||z_{student})$$

举得例子不知恰不恰当： 取A为学生模型，剩余部分的百分之多少为教师模型，进行蒸馏学习。

 第二篇去中心化交互迁移的联邦学习在物联网系统中应用。

Def-KT：

提出的原因

1.对于不同的模型直接平均，可能会产生客户漂移-----异构
2. 可以缩减通信成本和保证数据隐私
3. 中心服务器各方面都很强，很难找到。
4. 可以解决单个点失败的情形，增强稳定性。

引用${}^2$（熵平均）

Gossip算法被称反熵，熵是物理学上的一个概念，代表杂乱无章，而反熵就是在杂乱无章中寻求一致，这充分说明了Gossip的特点：在一个有界网络中，每个节点都随机的与其他节点通信，经过一番杂乱无章的通信，最终所有节点的状态都会达成一致。每个节点可能知道所有其他节点，也可能仅知道几个邻居节点。只要这些节点可以通过网络连通，最终他们的状态都是一致的，当然这个也是疫情传播的特点。Gossip 平均用在深度学习模型中，有很好的收敛性质。
原文链接.

针对客户漂移

1. 多中心聚合
2. 缩减方差，降低在更新过程的不良影响

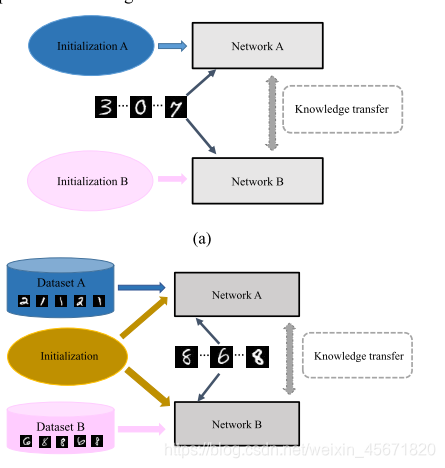
蒸馏

两个学生网络学习同一个数据集，另一个教另一个学习，初始化不同，学到更多知识。

假设：

1. 训练阶段的每一轮，仅有小部分子集合参与
2. 仅有小部分子集合的部分在本地数据集参与到训练本地模型，传递微调模型给其他集合。
3. 训练初始化相同

$D_k=(x_i{}^k,y_i^k)$, y i k ∈ { 1 , 2 , 3 , . . , C } y_i^k \in \{1,2,3,..,C\} yik​∈{1,2,3,..,C}, $N_k$ 表示第k个用户的训练总数， P k 表 示 不 同 的 分 布 ， k ∈ { 1 , 2 , . . . , K } P_k表示不同的分布，k \in \{1,2,...,K\} Pk​表示不同的分布，k∈{1,2,...,K} .

第t轮，随机选择Q个用户（2Q<<K）, 定义为 I t A = { k t 1 , k t 2 , . . . , k t Q } I_t^A =\{k_t^1,k_t^2,...,k_t^Q\} ItA​={kt1​,kt2​,...,ktQ​},Q中的每一个用户在私有集$D_{k_t^j}t$做M步训练，批大小为$B_1$,更新模型$w_t^{k_t^j}$, 记为
$${\dot{w}}_t^{k_t^j}<-SG{D}_{B_1,M}(w_t^{k_t^j},D_{k_t^j})\dots \dots \dots \dots \dots \dots (1)$$

$$P_{1,l}=model(B_l,{\dot{w}}_t^{k_t^j}),P_{2,l}=model(B_l,{\dot{w}}_t^{k_t^{j+Q}})$$

损失函数：
$$Los{s}_1({\dot{w}}_t^{k_t^j}),B_l,P_{2,l})=L_c(P_{1,l},y_l)+D_{kl}(P_{2,l}||P_{1,l})$$

$$Los{s}_2({\dot{w}}_t^{k_{j+Q}^j}),B_l,P_{1,l})=L_c(P_{2,l},y_l)+D_{kl}(P_{1,l}||P_{2,l})$$

$L_c,D_{KL}$公式就不展开了,

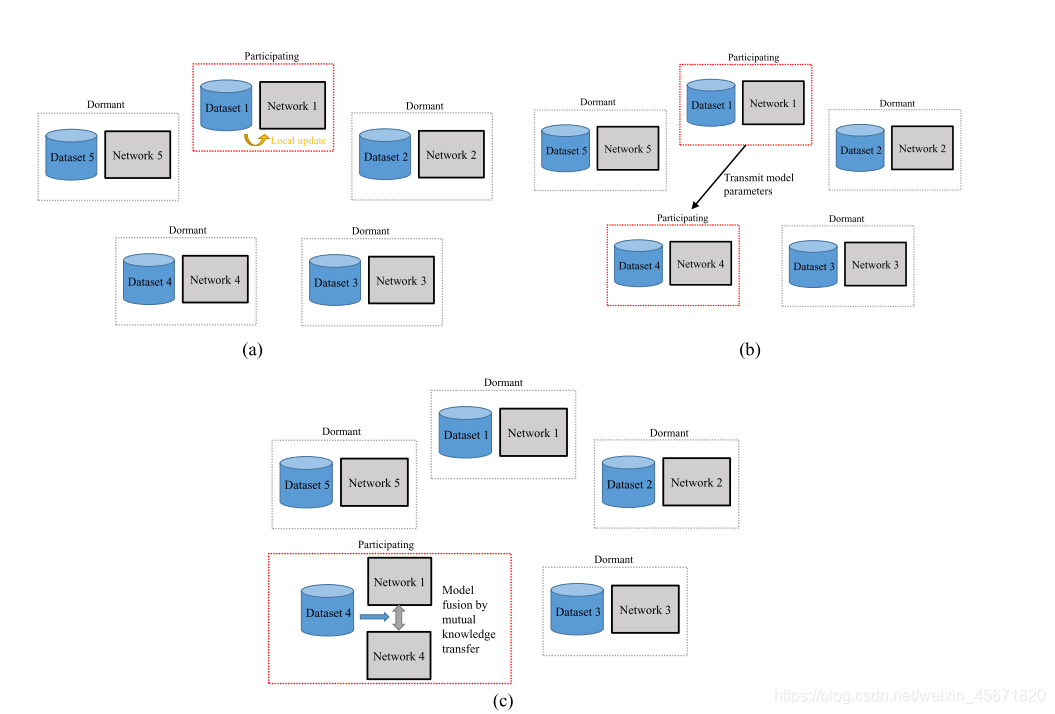
对于上图白话解释：
1.2Q分成两组， I t A = { k t 1 , k t 2 , . . . , k t Q } I_t^A =\{k_t^1,k_t^2,...,k_t^Q\} ItA​={kt1​,kt2​,...,ktQ​}， I t B = { k t Q + 1 , k t Q + 2 , . . . , k t 2 Q } I_t^B = \{k_t^{Q+1},k_t^{Q+2},...,k_t^{2Q}\} ItB​={ktQ+1​,ktQ+2​,...,kt2Q​}

2.$I_t^A$组中的用户训练模型，将权重参数传输到对应的$I_t^B$组中的某一用户
3. $I_t^B$中的用户以$B_2$大小分割数据集
4. 对初始参数$I_t^A$传输的参数在本地数据集上计算激活函数softmax $P_{1,l},P_{2,l}$
5. 在k+Q上更新${\dot{w}}_t^{k_t^j}$ 和$w_t^{k_t^{j+Q}}$
6. ${\dot{w}}_t^{k_t^j}$存储在$k_t^{j+Q}$中
7. 收敛时，停止

这里是加权平均

这是发一半，各算各的。

优势

1. 间接从看不见的数据学习
2. 通过对具有不同专长的模型的知识进行综合，提高泛化能力。
3. 灾难性遗忘
4. 避免不同模型的同质化

以上是两篇去中心化的回顾。