往期博客:
目录
题目
给你一个整数数组
nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
题目分析
已知:整数数组 nums
目的:找出最大和的连续子数组
要求:返回最大和
示例
示例1
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例2
输入:nums = [1] 输出:1
示例3
输入:nums = [5,4,-1,7,8] 输出:23
解析
暴力法
对于给定的数组,我们可以逐一从数组中去取元素,然后计算所有情况下元素的和,从而找到最大的和。
例如,对于数组nums=[-2,1,-3,4,-1,2],首先构建两个指针 i 和 j ,其中 i 和 j 指向第一个元素,逐步移动 j 并取出 j 指向的元素,知道 j 指向末尾时,将 i 指向第二个元素,同样将 j 从此时的 i 处开始进行移动,并取出元素,依次进行,直到 i 移动到结尾。
然后计算res中元素的和,从而选出最大的和
分治法
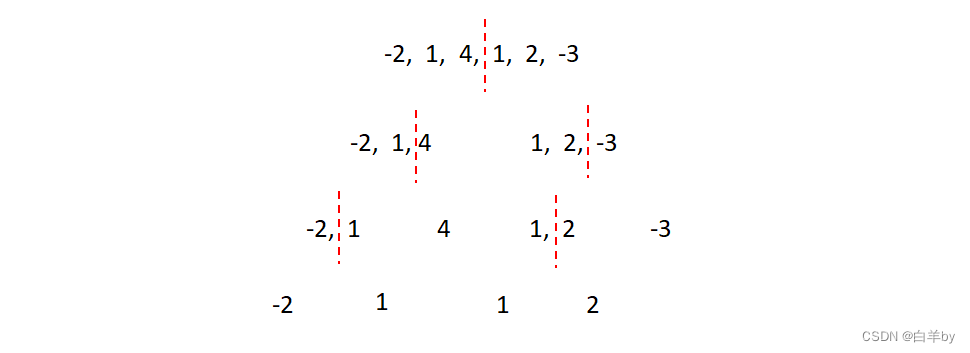
分治法是将整个数组分成左右两个部分,分别找到左右两个部分的最大子序列的和a和b,然后再对比a、b和a+b,从而找到最大的子序列的和。
通过例子我们可以看到,最大子序列要么在左边,要么在右边,要么横跨左右两边,所以使用分治法,将整个数组分解成一个一个小的问题来解决。
将整个数组不断地从中间进行拆分,直到剩一个元素为止
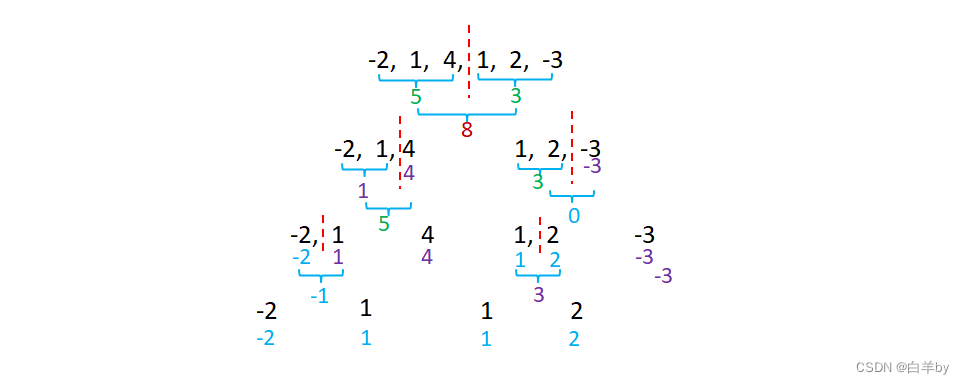
然后从下到上进行最大子序列和的查找
动态规划
动态规划法是从头开始分别将元素和前面所有元素中的最大子序列进行联系,此时的联系包括合并和比较。
- 当前元素和前面所有元素中的最大子序列合并——当前元素和合并后的和进行比较
- 当前元素和前面所有元素种的最大子序列不合并——当前元素和和前面所有元素中的最大子序列的和进行比较
此时便找出了每个动态过程中的最大子序列的和,分贝比较每个最大子序列的和,从而找到整个数组的最大子序列的和
我们可以总结出动态规划的三个要素
代码
暴力法
时间复杂度:O(N^2)
空间复杂度:O(1)
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
result = float('-inf')
for i in range(0, len(nums)):
temp = 0
for j in range(i, len(nums)):
temp = temp + nums[j]
result = max(result, temp)
return result分治法
时间复杂度:O(N)
空间复杂度:O(logN)
class Solution:
# Time Complexity: O(N)
# Space Complexity: O(logN)
def maxSubArray(self, nums: List[int]) -> int:
return self.getMax(nums, 0, len(nums)-1)
def getMax(self, nums, l, r):
if l == r:
return nums[l]
mid = l + (r-l)//2
leftSum = self.getMax(nums, l, mid)
rightSum = self.getMax(nums, mid+1, r)
crossSum = self.crossSum(nums, l, r)
return max(leftSum, rightSum, crossSum)
def crossSum(self, nums, l, r):
mid = l + (r-l)//2
# from mid to leftmost
leftSum = nums[mid]
leftMax = leftSum
for i in range(mid-1, l-1, -1):
leftSum += nums[i]
leftMax = max(leftMax, leftSum)
# from mid to rightmost
rightSum = nums[mid+1]
rightMax = rightSum
for i in range(mid+2, r+1):
rightSum += nums[i]
rightMax = max(rightMax, rightSum)
return leftMax + rightMax动态规划
时间复杂度:O(N)
空间复杂度:O(N)
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
dp = [0]*len(nums)
dp[0] = nums[0]
result = nums[0]
for i in range(1, len(nums)):
dp[i] = max(dp[i-1] + nums[i], nums[i])
result = max(result, dp[i])
return result