哈夫曼编码与哈夫曼算法

哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码（有时也称为霍夫曼编码）

哈夫曼编码在文件压缩上的应用：

哈夫曼编码可以运用在对文件字符的编码上，以实现对文件的压缩。
加入一个文件中存在a,b,c,d,e这几种字符，文件的整体是由这5中字符构成的，如果我们要用二进制编码这个文件，那么就需要对每一个字符分别进行二进制编码来对它们进行区分。
假设这5中字符在文件中出现的频率分别是：5，12，6，3，9
如果我们用一般的方式来进行编码，要使用同长度的2进制码区分五种字符，那么我们需要长度为3bit的编码来表示，即
a——000；b——001；c——010；d——011；e——100；
这样对文件中的字符编码在正确性上是没有问题的，但是我们可以计算出文件编码后的总大小为：35*3=105bit

哈夫曼编码用特殊的编码方式来使这样的文件在编码后占用的bit总数更小：
哈夫曼编码的特殊性在于，使字符编码的长度可以不相同，对应上面的例子来说也就是说每一个字符的二进制编码表示不一定长度都为3。
如果我们才用以下这样的方式去编码这文件中的5个字符：
a——000；b——01；c——10；d——001；e——11；
那么我们再次计算一下编码后文件的总大小：35+212+26+33+2*9=78bit
结果明显比一般的同长度的编码方式减小了。但是要注意，这样的编码方式使每个字符编码不存在二义性的前提是每一个字符编码都不能是其他字符编码的前缀。

如何获得哈夫曼编码（最优编码）

通过构造哈夫曼树获得哈夫曼编码：

1.哈夫曼树
哈夫曼树是这样的一棵树：给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

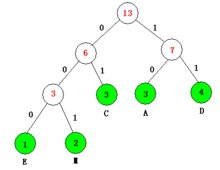
简单的来讲，就是说哈夫曼树是要使树中的每一个节点的权值与这个节点的深度的乘积的和最小的树。那么其实这样的哈夫曼树的特点就是，权值越大的节点离根节点越近，拥有较小的深度，而权值最大的节点往往就作为根节点；权值越小的节点离根节点越远，权值最小的树一定是叶子节点。 上图所示就是一颗哈夫曼树，也称作最优二叉树。

2.哈夫曼算法

最优哈夫曼编码树的创建

我们可以通过以下哈夫曼算法来创建一颗最优哈夫曼编码树：
对于我们最开始举得例子而言，一共存在5个字符a，b，c，d，e，且其出现的频率分别为：5，12，6，3，9
我们将每一个字符设置为一个节点，并且这个节点的权值就是字符出现的频率。
现在我们将每一个单独的节点看作是一棵树，这样一来我们就得到了一个森林。
森林中一共有5棵树，a，b，c，d，e，树的权值分别为5，12，6，3，9.
在算法的开始，我们首先找到森林中任意两颗权值最小的树，并将它们分别作为新树的两个孩子节点来合并，其中左右孩子节点的顺序可以是任意的。这里我们就找到了节点a和d，将它们作为树T1的两个孩子节点得到新树T1，重复这样的过程，直到全部单节点树都被合并，最终整个森林合并为一棵树为止。此时我们得到树就是最优哈夫曼编码树。
我们可以通过哈夫曼编码树得到哈夫曼编码，方法是从根节点开始到任意一个叶子节点的路径上，如果经过向左的分支则得到0，经过向右的分支则得到1，用上图中的哈夫曼树举例子，叶子节点E的编码即为000，叶子节点A的编码即为01.
下面我们给出得到最优哈夫曼编码树的c语言代码：

#include <stdio.h>
#include <stdlib.h>
//定义哈夫曼树和节点 
typedef struct HTreeNode
{
	char ch;
	int weight;
	struct HTreeNode *left;
	struct HTreeNode *right;
}HTreeNode,*HTree;
//定义森林 
typedef struct forest
{
	int tree_num;
	int *book;
	int *weight;
	HTreeNode *trees;
}forest;
//初始化森林 
forest *Init_forest(int tree_num)
{
	int i,ch,weight;
	forest * f=(forest*)malloc(sizeof(forest));
	f->tree_num=tree_num;
	f->book=(int *)calloc(tree_num,sizeof(int));
	f->weight=(int *)calloc(tree_num,sizeof(int));
	f->trees=(HTreeNode *)calloc(tree_num,sizeof(HTreeNode));
	for(i=0;i<tree_num;i++)
	{
		printf("\n请输入字符：");
		scanf("%c",&ch); getchar();
		printf("\n请输入字符出现频率：");
		scanf("%d",&weight); getchar();
		f->trees[i].ch=ch;
		f->trees[i].weight=weight;
		f->weight[i]=weight;
		f->trees[i].left=NULL;
		f->trees[i].right=NULL;
	}
	return f;
}
//在遍历树的过程中计算树的权值 
void OrderTree(HTree t,int * weight,int depath)
{
	if(t->left==NULL&&t->right==NULL)
	{
		(*weight)+=(t->weight)*depath;
		return;
	}
	OrderTree(t->left,weight,depath+1);
	OrderTree(t->right,weight,depath+1);	
}
//得到树的权值 
int get_weight(HTree t)
{
	int weight=0;
	OrderTree(t,&weight,0);
	return weight;
}
//合并两棵树
int UnionTrees(forest *f)
{
	
	HTree t1=NULL,t2=NULL,t3=(HTree)malloc(sizeof(HTreeNode));
	HTree leftchild=(HTree)malloc(sizeof(HTreeNode)),rightchild=(HTree)malloc(sizeof(HTreeNode));
	int index1,index2;
	int i,j,k;
	int min_weight,index;
	for(k=1,i=0;k<=2;k++,i=0)
	{
	while(f->weight[i]==0||(&f->trees[i])==t1) i++;	
	index=i;
	min_weight=f->weight[i];
	for(i=0;i<f->tree_num;i++)
	{
		if((&f->trees[i])==t1) continue;
		if(min_weight>f->weight[i]&&f->weight[i]!=0)
		{
			
			min_weight=f->weight[i];
			index=i;
		}
	}
	if(k==1) 
	{
	    t1=&(f->trees[index]);
	    index1=index;
    }
	else 
	{
		t2=&(f->trees[index]);
		index2=index;
	}	
}
    *leftchild=*t1;
    *rightchild=*t2;
    t3->left=leftchild;
	t3->right=rightchild;
	//t3->weight=get_weight(t3);
	t3->weight=t1->weight+t2->weight;
	f->trees[index1]=*t3;
	f->weight[index1]=t3->weight;
	f->weight[index2]=0;
 return index1;
}
//遍历哈夫曼树以得到哈夫曼编码 
void get_code(HTree t,int code[],int step)
{
	if(t==NULL) return;
	if(t->left==NULL&&t->right==NULL)
	{
		int i=0;
		for(i=0;i<step;i++) printf("%d ",code[i]);
		printf(" %c\n",t->ch);
		return;
	}
		code[step]=0;
		get_code(t->left,code,step+1);
		code[step]=1;
		get_code(t->right,code,step+1);
 } 
//Huffman算法
Huffman(forest *f) 
{
	HTree ht;
	int i,j,k,index;
	int n=f->tree_num,code[n];
	for(i=0;i<n-1;i++)
	{
		index=UnionTrees(f);//将森林中的n棵树合并n-1次最后得到最优的那颗Huffman树 
	}
	ht=&f->trees[index];
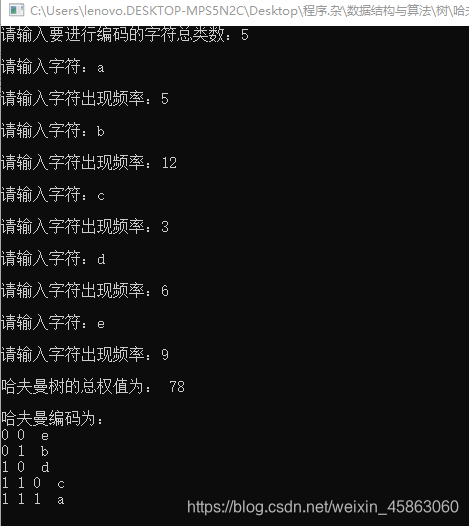
	printf("\n哈夫曼树的总权值为： %d \n",get_weight(ht));
	printf("\n哈夫曼编码为：\n");
	get_code(ht,code,0);
}
main()
{
    int n,i,j,k;
    printf("请输入要进行编码的字符总类数：");
    scanf("%d",&n);
    getchar();
    forest *f=Init_forest(n);
    Huffman(f);
}