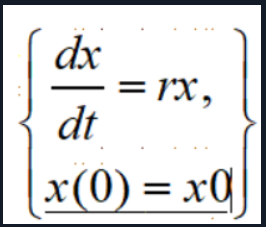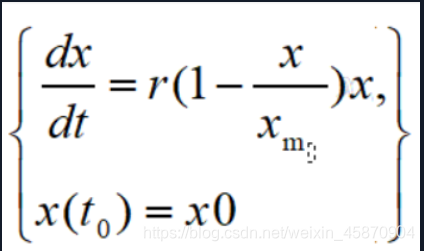Malthus模型

这是英国神父Malthus通过对一百多年人口统计资料的分析之后提出的人口模型假设

模型假设

1. 设x(t)表示t时刻的人口数，且x(t)连续可微.
2. 人口的增长率r是常数(增长数=出生率-死亡率)
3. 人口的数量的变化是封闭的，即人口数量的增加与减少只取决于人口中个体的生育和死亡，且每一个体都具有同样的生育能力与死亡率.

建模与求解

由假设，t时刻到t+△t时刻人口的增量为x(t+△)-x(t)=rx(t)△t.

​ 所以得到

import sympy as sp
from sympy import  diff,dsolve,simplify
x=sp.symbols('x',cls=sp.Function)
t=sp.symbols('t')
r=sp.symbols('r')
eq=diff(x(t),t)-(r*x(t))
x=dsolve(eq)
print(simplify(x))

所以其解为：

​ $$x(t)=x0e^{r}t$$

模型评价

考虑二百多年来人口增长的实际情况，1961年世界人口总数为$$3.06\times 10^9$$,我们对人口自然增长率设置为2%.
so $$x(t)=3.06\times 10^9\cdot e^{0.02(t-1961)}$$

这一模型符合1961年前的历史人口增长，但对于未来人口数量增长统计却存在一定的极端和不准确性，所以对于r是常数这个地方是值得商榷的.

Logistic模型

继上个模型，我们现在来对r进行修正，因为地球上的资源是有限的，所以随着人口数量的增加，自然资源和环境条件对于人口增长的限制作用将会逐渐显著.

所以，我们将r视为一个随着人口的增加而减小的量，即将增长率r表示为人口x(t)的函数r(x),且r(x)为x的减函数.

模型假设

1. 设r(x)为x的线性函数，r(x)=r-sx(工程师原则，首先用线性).
2. 自然资源与环境条件所能容纳的最大人口数$\chi_m $ 即当$\chi ={\chi }_m$时，增长率r(${\chi }_m$)=0.

建模与求解

​ 由假设(1),(2)可得$$r(x)=r(1-\frac{\chi }{{\chi }_m})$$,则有

import sympy as sp
import math
from sympy import  diff,dsolve,simplify
x=sp.symbols('x',cls=sp.Function)
t=sp.symbols('t')
r=sp.symbols('r')
xm=sp.symbols('xm')
c1=sp.symbols('c1')
x0=sp.symbols('x0')
eq=diff(x(t),t)-r*(1-(x(t)/xm))*x(t)
x=dsolve(eq)
print(simplify(x))

求解方程得到 $$Eq(x(t),-xm/(exp(C1\ast xm-r\ast t)-1))$$

其中因为C1较为复杂所以这里用python求解并不是一直好办法

我们直接用分离变量法求解 得到x(t)

$$x(t)=\frac{xm}{1+(\frac{xm}{x0}-1)e^{-r(t-t0)}}$$

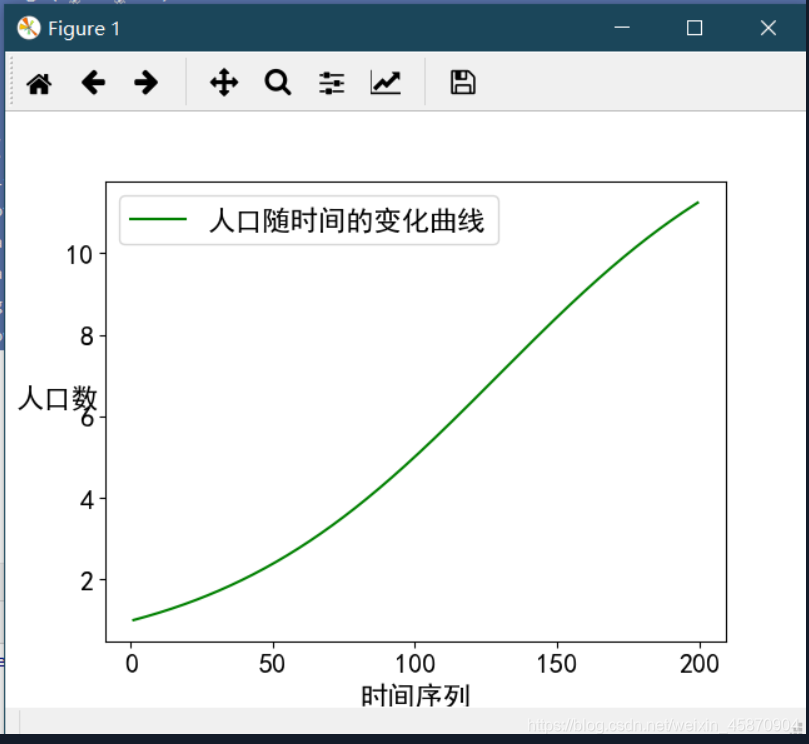
我们用pyplot来使得x(t)函数可视化

import matplotlib.pyplot as plt
import numpy as np
import math
t=np.arange(1,200,0.5)
xm=14
x0=1 #防止除0错误
t0=1 #防止除0错误
r=0.02
plt.rc('font',size=16); plt.rc('font',family='SimHei')
y=xm/(1+(xm/x0-1)*pow(math.e,-r*(t-t0)))
plt.plot(t,y,'g',label='人口随时间的变化曲线')
plt.xlabel("时间序列")
plt.ylabel("人口数",rotation=0)
plt.legend()
plt.show()

可以看到用logistic模型解出的回归函数会更加科学

模型检验

$$\frac{d^{2}x}{d{t}^2}=r^2(1-\frac{x}{xm})(1-\frac{2x}{xm})x$$

所以人口总数x(t)有如下规律:

1. ${\lim }_{t\to +\infty }\chi (t)={\chi }_m$, 即无论人口初值 ${\chi }_0$ 如何，人口总数以${\chi }_m$为极限。

2. 当$0<{\chi }_0<{\chi }_m$ 时 $\frac{d_x}{d_t}=r(1-\frac{\chi }{{\chi }_m})x>0$ ， 这说明x(t)是单调增加的。
   根据$\frac{d^{2}x}{d{t}^2}=r^2(1-\frac{x}{xm})(1-\frac{2x}{xm})x$
   说明当$x<\frac{x_m}{2}$时，$\frac{d^{2}x}{d{t}^2}>0$ x=x(t)是一个凹函数

   而当$x<\frac{x_m}{2}$的时候 $\frac{d^{2}x}{d{t}^2}<0$ x=x(t)是一个凸函数

3. 人口变化率 $\frac{d_x}{d_t}$ 在$x=\frac{x_m}{2}$时取到最大值，即人口总数达到极限值一半以前是加速生长时期，经过这一点以后，增长速率会逐渐变小，最终达到零。

以上的结论都可以从上面我画的曲线中直观地看出.