图解LeetCode09：回文数，多种解法

LeetCode09：回文数

给你一个整数x，如果x是一个回文整数，返回true；否则，返回false

回文数是指正序（从左到右）和倒序（从右向左）读都是一样的整数。例如，121是回文，123不是回文。

示例：

输入：x = 121
输出：true

输入：x = -121
输出：false
解释：从左到右是-121。从右向左是121-，所以不是回文数

提示：

-2^31 < x < 2^31 - 1

进阶：你能不将整数转为字符串来解决这个问题吗？

解法1：

首先，不考虑进阶，我们可以将其转换为字符串进行处理

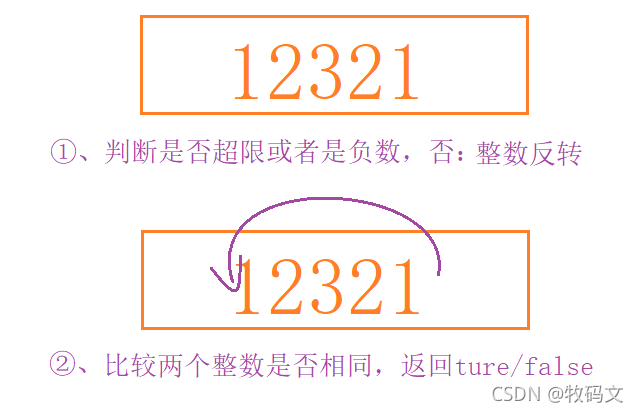
分析题目可以知道，对于一个整数x，如果为负数，则一定不会是回文数，所以可以将题解分为以下几步

①、判断是否是负数以及是否超限，是就返回false，否转为字符串

②、维护两个指针，分别从左到右和从右到左比较，全部一致为true，如不一致返回false
在这里插入图片描述

代码

public boolean judgeReturn(int x){
    // 判断x是否超限或者负数
    if (x < 0 || x > (long)(Integer.MAX_VALUE)) return false;
    // 转换为字符串
    String s = String.valueOf(x);
    // 维护两个指针，分别遍历
    for (int i = 0, j = s.length() - 1; i < j; i++, j--){
        // 如果不等，返回false
        if (s.charAt(i) != s.charAt(j)) return false;
    }
    // 回文，返回true
    return true;
}

解法2：

因为进阶中要求不转为字符串求解，所以就要利用一个整数求解

思路1：

比较简单粗暴的方法，将整数反转，然后与整数x比较，一致就返回true，否则返回false
在这里插入图片描述
代码

public boolean judgeReturn2(int x){
        // 判断x是否超限或者负数
        if (x < 0 || x > (long)(Integer.MAX_VALUE)) return false;

        // 反转字符
        int ans = 0, pop = 0;
        int m = x;
        while(m != 0){
            pop = m % 10;
            ans = ans * 10 + pop;
            m = m / 10;
        }
        return ans == x;
    }

上述的代码存在问题，因为是整数反转，所以涉及到整数反转超限的问题，因为不考虑使用这种方法，所以没有进行反转超限的判断，知识写了这个代码说明一下这个思路

思路2：

为了避免数字反转之后导致的溢出问题，我们可以仔细的分析回文数字的特点，可以借鉴转为字符串的分析方法，当转为字符串是从两边分别遍历开始比较的时候，为什么比较到一半就可以得到答案？

我们看一下回文数的特点
在这里插入图片描述

我们可以看到回文数是左右对称的，也就是我们只需要将左边或者右边的数字反转，然后再与对称的边比较，如果相等，就是回文数；否则就不是

那么怎么比较呢？

我们只需要将右边的数字逐一反转
在这里插入图片描述
关于反转在LeetCode07：整数反转已经是很详细了通过

pop = x % 10 ----> 得到个位数
ans = ans * 10 + pop ----> 得到反转数
// 而剩下的就是前半部分的数字
x = x / 5 ----> 前半部分的数值

那么问题就变成了，怎么确定一个数字的中间位置

整数的中间位置怎么确定？？？

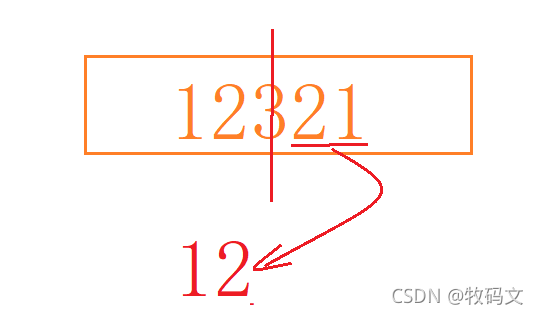
比如整数12321，当我们不断的遍历去除个位数反转的时候，就有两个数值

第一次取出个位数：ans = 1; x = 1232
第二次取出个位数：ans = 12; x = 123;
第三次取出个位数：ans = 123; x = 12;
// 这个时候，当ans > x ，就说明取出了中间位置的数字

在这里插入图片描述

代码

public boolean judgeReturn3(int x){
        // 判断x是否超限或者负数
        if (x < 0 || x > (long)(Integer.MAX_VALUE)) return false;
        // ans为后段反转字符
        int ans = 0;
        while (x > ans){
            ans = ans * 10 + x % 10;
            x = x/10;
        }
        return ans == x || ans/10 == x;
    }

测试

public static void main(String[] args) {
        LeetCode09 lc = new LeetCode09();
        System.out.println(lc.judgeReturn(12121));
        System.out.println(lc.judgeReturn2(12121));
        System.out.println(lc.judgeReturn3(12121));
    }

结果

true
true
true