主题与背景
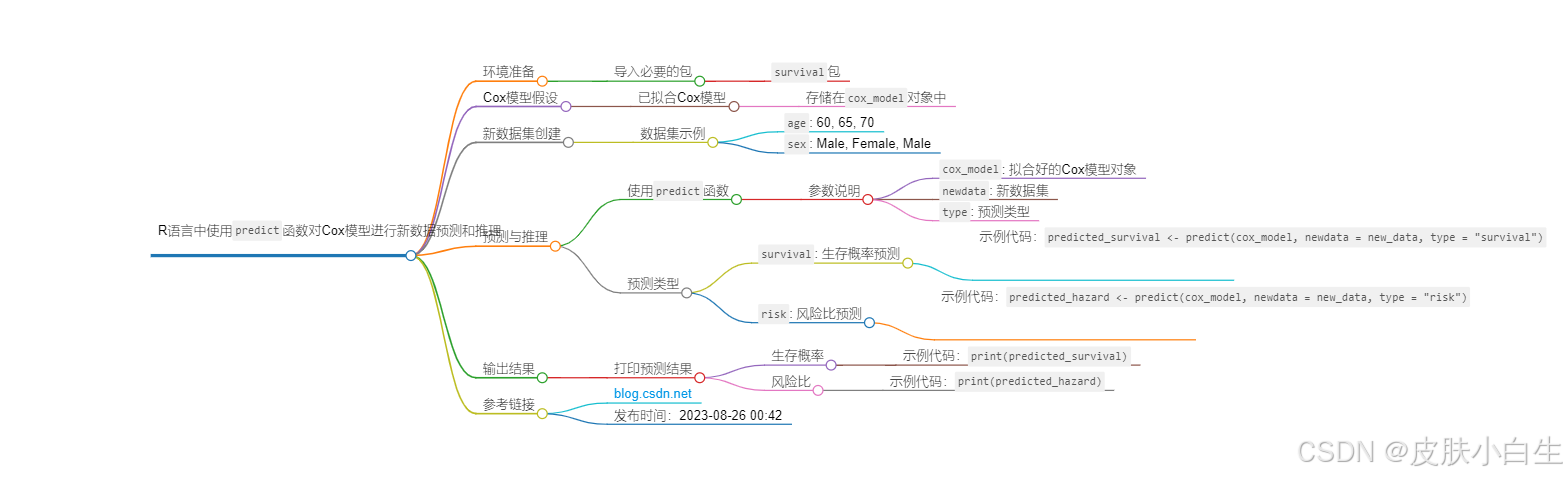
本文主要介绍了如何在R语言中使用predict函数对已拟合的Cox比例风险模型进行新数据的预测和推理。Cox模型是一种常用的生存分析方法,用于评估多个因素对事件发生时间的影响。文章通过具体的代码示例展示了如何使用predict函数的不同参数来获取生存概率和风险比。
主要观点
导入survival包
首先需要导入R语言中的survival包,该包提供了实现Cox比例风险模型和其他生存分析方法的功能。
假设已有Cox模型
假设已经有一个Cox模型,并将其存储在cox_model对象中。这个模型是通过之前的数据拟合得到的。
创建新数据集
为了进行预测,需要创建一个新的数据集new_data。在这个例子中,新数据集包含两列:年龄(age)和性别(sex),分别对应三个新的个体。
使用predict函数进行预测
生存概率预测:
使用predict函数并设置type = "survival"来预测新数据的生存概率。这将返回每个新个体在特定时间点的生存概率。
风险比预测:
使用predict函数并设置type = "risk"来预测新数据的风险比。这将返回每个新个体的风险比,表示相对于参考水平的风险增加或减少的程度。
打印预测结果
最后,文章展示了如何打印出预测的生存概率和风险比,以便进一步分析和解释。
# 导入必要的包
library(survival)
# 创建一个包含更多变量的数据集
set.seed(123) # 为了可重复性设置随机数种子
data <- data.frame(
time = c(5, 8, 10, 4, 12, 7, 9, 6, 13, 11), # 生存时间
status = c(1, 0, 1, 0, 1, 1, 0, 1, 0, 1), # 结局状态:1表示事件发生,0表示删失
age = c(60, 65, 70, 55, 80, 72, 60, 68, 75, 65), # 年龄
sex = c("Male", "Female", "Male", "Female", "Male", "Female", "Male", "Female", "Male", "Female"), # 性别
smoking_status = c("Smoker", "Non-smoker", "Non-smoker", "Smoker", "Smoker", "Non-smoker", "Smoker", "Non-smoker", "Smoker", "Non-smoker"), # 吸烟状态
treatment = c("DrugA", "DrugB", "DrugA", "DrugA", "DrugB", "DrugA", "DrugB", "DrugA", "DrugB", "DrugA") # 治疗类型
)
# 将分类变量转化为因子变量
data$sex <- factor(data$sex, levels = c("Male", "Female"))
data$smoking_status <- factor(data$smoking_status, levels = c("Smoker", "Non-smoker"))
data$treatment <- factor(data$treatment, levels = c("DrugA", "DrugB"))
# 拟合Cox回归模型
cox_model <- coxph(Surv(time, status) ~ age + sex + smoking_status + treatment, data = data)
# 打印Cox模型结果
summary(cox_model)
# 创建新的数据集进行预测
new_data <- data.frame(
age = c(60, 65, 70),
sex = c("Male", "Female", "Male"),
smoking_status = c("Smoker", "Non-smoker", "Smoker"),
treatment = c("DrugA", "DrugB", "DrugA")
)
# 将新的数据集的分类变量转换为因子
new_data$sex <- factor(new_data$sex, levels = c("Male", "Female"))
new_data$smoking_status <- factor(new_data$smoking_status, levels = c("Smoker", "Non-smoker"))
new_data$treatment <- factor(new_data$treatment, levels = c("DrugA", "DrugB"))
# 使用predict函数进行生存概率和风险预测
predicted_survival <- predict(cox_model, newdata = new_data, type = "survival")
predicted_hazard <- predict(cox_model, newdata = new_data, type = "risk")
# 打印预测结果
cat("预测的生存概率:\n")
print(predicted_survival)
cat("\n预测的风险比:\n")
print(predicted_hazard)
总结
本文详细介绍了在R语言中使用predict函数对Cox比例风险模型进行新数据预测的具体步骤。核心观点包括导入必要的包、准备新数据集、使用predict函数的不同参数(type = "survival" 和 type = "risk")来进行生存概率和风险比的预测,以及如何输出和查看这些预测结果。通过这些步骤,用户可以有效地利用已有的Cox模型对新数据进行生存分析和风险评估。
cox 代码如下:
# 加载所需的库
library(rms)
library(timeROC)
# 假设我们的随访时间变量是 time, 结局状态变量是 status,并且我们有两个预测变量 predictor1 和 predictor2
如果是分类变量,需要设置为factor, 并加上文字标签,连续性变量不用管,例如:
train_data$predictor1<-factor(train_data$predictor1,levels = c(0,1),labels = c('No','Yes'))
train_data$predictor2<-factor(train_data$predictor2,levels = c(1,2,3),labels = c('Stage I','Stage II','Stage III'))
# 设置模型公式
formula <- Surv(time,status) ~ predictor1 + predictor2
# 首先,我们需要为我们的数据设置一个数据分布对象
# 这会帮助rms包更好地理解我们的数据结构
options(datadist=NULL)
ddist <- datadist(train_data)
options(datadist = 'ddist')
# 现在我们可以在训练数据上拟合Cox回归模型
model <- rms::cph(formula, data = train_data, surv = T,x = TRUE, y = TRUE)
# 在训练集上生成预测值
train_predvalue <- predict(model, newdata = train_data)
# 在训练集上生成ROC对象
roc_train <- timeROC::timeROC(T=train_data$time,
delta=train_data$status,
marker=train_predvalue,
cause=1,
weighting='marginal',
times=c(365.25*1,365.25*3,365.25*5),
iid=TRUE)
# 求auc和可信区间
roc_train$AUC
confint(roc_train)$CI_AUC
# 绘制曲线
plot(roc_train,
time=365.25*1,
lty=1,lwd=2,
xlab='1-Specificities',ylab='Sensitivities',
col = 'red',
title='')
plot(roc_train,
time=365.25*3,
lty=1,lwd=2,
xlab='1-Specificities',ylab='Sensitivities',
col = 'red',
title='')
plot(roc_train,
time=365.25*5,
lty=1,lwd=2,
xlab='1-Specificities',ylab='Sensitivities',
col = 'red',
title='')
# 在内部验证集上生成预测值
validation_predvalue <- predict(model, newdata = validation_data)
# 在训练集上生成ROC对象
roc_validation <- timeROC::timeROC(T=validation_data$time,
delta=validation_data$status,
marker=validation_predvalue,
cause=1,
weighting='marginal',
times=c(365.25*1,365.25*3,365.25*5),
iid=TRUE)
# 求auc和可信区间
roc_validation$AUC
confint(roc_validation)$CI_AUC
# 绘制曲线
plot(roc_validation,
time=365.25*1,
lty=1,lwd=2,
xlab='1-Specificities',ylab='Sensitivities',
col = 'red',
title='')
plot(roc_validation,
time=365.25*3,
lty=1,lwd=2,
xlab='1-Specificities',ylab='Sensitivities',
col = 'red',
title='')
plot(roc_validation,
time=365.25*5,
lty=1,lwd=2,
xlab='1-Specificities',ylab='Sensitivities',
col = 'red',
title='')
# 在外部验证集上生成预测值
external_predvalue <- predict(model, newdata = external_data)
# 在训练集上生成ROC对象
roc_external <- timeROC::timeROC(T=external_data$time,
delta=external_data$status,
marker=external_predvalue,
cause=1,
weighting='marginal',
times=c(365.25*1,365.25*3,365.25*5),
iid=TRUE)
# 求auc和可信区间
roc_external$AUC
confint(roc_external)$CI_AUC
# 绘制曲线
plot(roc_external,
time=365.25*1,
lty=1,lwd=2,
xlab='1-Specificities',ylab='Sensitivities',
col = 'red',
title='')
plot(roc_external,
time=365.25*3,
lty=1,lwd=2,
xlab='1-Specificities',ylab='Sensitivities',
col = 'red',
title='')
plot(roc_external,
time=365.25*5,
lty=1,lwd=2,
xlab='1-Specificities',ylab='Sensitivities',
col = 'red',
title='')