1.求複合函數的定義域
**定义**:
若函数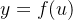
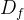
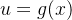
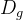
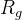

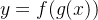
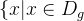
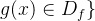
**例题 1**:
已知
![[0, 2]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIwJTJDJTIwMiU1RA%3D%3D)
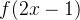
**解**:令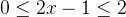
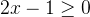
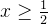
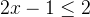
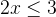
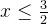
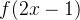
![[\frac{1}{2}, \frac{3}{2}]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIlNUNmcmFjJTdCMSU3RCU3QjIlN0QlMkMlMjAlNUNmcmFjJTdCMyU3RCU3QjIlN0QlNUQ%3D)
**例题 2**:
已知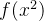
![[ - 1, 2]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIlMjAtJTIwMSUyQyUyMDIlNUQ%3D)

**解**:因为![x\in[-1, 2]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT94JTVDaW4lNUItMSUyQyUyMDIlNUQ%3D)
![x^2\in[0, 4]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT94JTVFMiU1Q2luJTVCMCUyQyUyMDQlNUQ%3D)

![[0, 4]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIwJTJDJTIwNCU1RA%3D%3D)
**例题 3**:
若
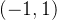
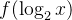
**解**:令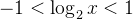
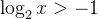
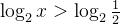
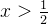
解不等式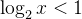
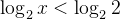
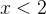
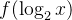
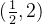
2.函數形態(原函數和導函數的連續和有界的關係)
**关系**:
1. 若
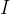
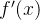
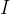

2.若
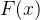
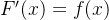
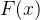
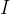

**例题 1**:

![[ - 1, 1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIlMjAtJTIwMSUyQyUyMDElNUQ%3D)

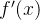
![[ - 1, 1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIlMjAtJTIwMSUyQyUyMDElNUQ%3D)
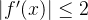

![[ - 1, 1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIlMjAtJTIwMSUyQyUyMDElNUQ%3D)
**例题 2**:

![(0, 1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lMjgwJTJDJTIwMSU1RA%3D%3D)

![(0, 1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lMjgwJTJDJTIwMSU1RA%3D%3D)
**例题 3**:



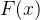

3.極限的概念
**定义(以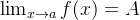 为例)**:
为例)**:
设函数

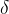
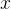
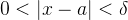

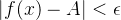
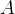


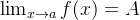
**例题 1**:
用定义证明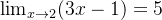
**证明**: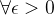
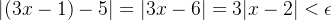
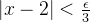

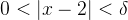
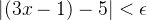
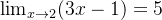
**例题 2**:
用定义证明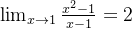
**证明**: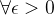
。取

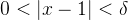
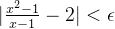
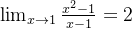
**例题 3**:
用定义证明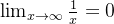
**证明**: