📖标题：How Numerical Precision Affects Mathematical Reasoning Capabilities of LLMs
🌐来源：arXiv, 2410.13857

摘要

🔸尽管基于转换的大型语言模型（LLMs）在各个领域取得了显著成功，但理解和提高其数学能力仍然是一个重大挑战。
🔸本文对LLMs的数学能力进行了严格的理论分析，特别关注他们的算术表现。我们认为数值精度是影响其在数学任务中有效性的关键因素。
🔸我们的结果表明，以低数值精度运行的变压器无法解决迭代加法和整数乘法等算术任务，除非模型大小相对于输入长度超多项式增长。相比之下，具有标准数值精度的变压器可以有效地处理这些任务，模型尺寸要小得多。我们通过实证实验进一步支持我们的理论发现，这些实验探索了不同数值精度对算术任务的影响，为提高LLM的数学推理能力提供了有价值的见解。

🛎️文章简介

🔸研究问题：低精度设置下，大语言模型（LLM）在执行基本算术任务时遇到显著挑战。
🔸主要贡献：论文系统地分析了数值精度对LLM数学推理能力的影响，并提供了理论和实践上的见解。

📝重点思路

🔺相关工作

🔸LLM数学推理：像GPT-4这样的高级模型生成的答案也不总是准确的，也没法准确验证解决过程，现有思路包括提示策略、数学微调、调用外部工具和自我验证等。
🔸LLM算术推理：算术推理是数学能力的关键组成部分，在数字顺序反转等任务都会遇到调整，现有思路包括改进位置编码，提高长度外推和数据格式泛化性。
🔸Transformer的计算能力：早期工作集中在函数逼近能力，证明了有限精度Transformer近似图灵完备，后续研究了形式语言能力以及思想链和情境学习的重要性。

🔺论文方案

🔸理论分析：通过构建和证明定理，探讨了不同精度设置下Transformer模型的表现，特别是对基本算术任务（如整数加法、迭代加法和整数乘法）的影响。
🔸实验验证：通过大量的实验来验证理论分析的结论，包括从头训练Transformer模型，并系统地评估问题规模和数值精度（如int8、float8和float32）对模型性能的影响。

🔎分析总结

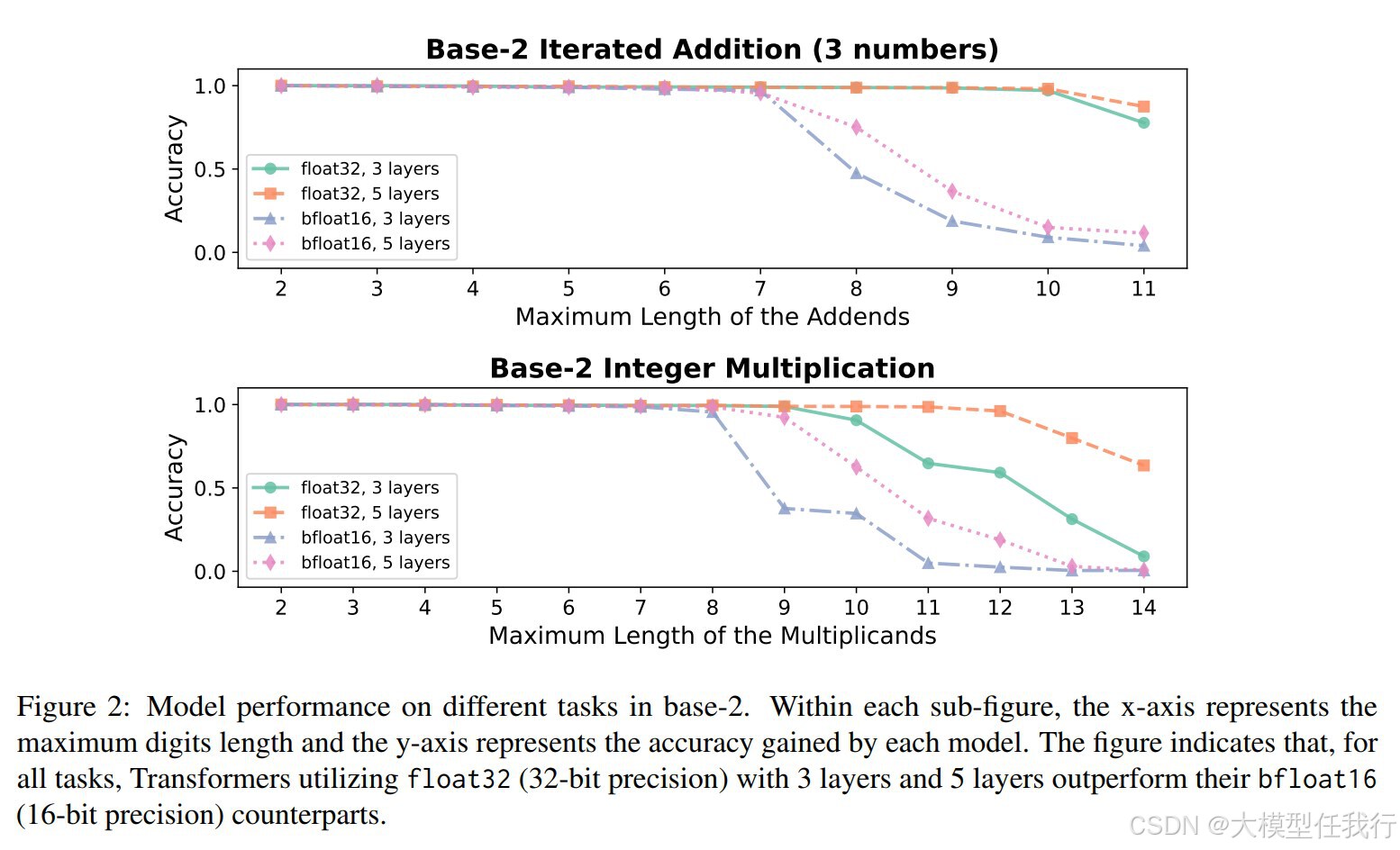
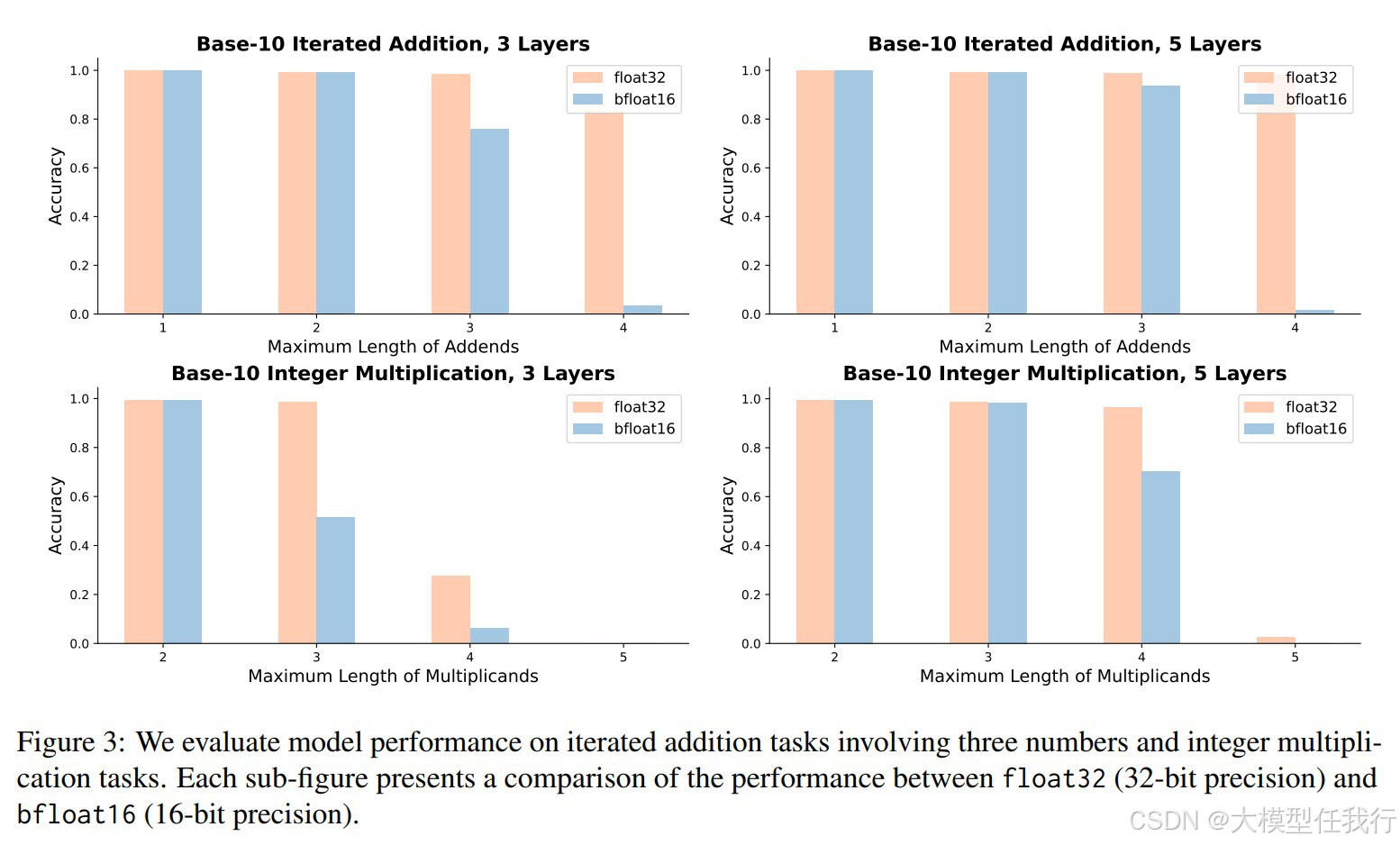
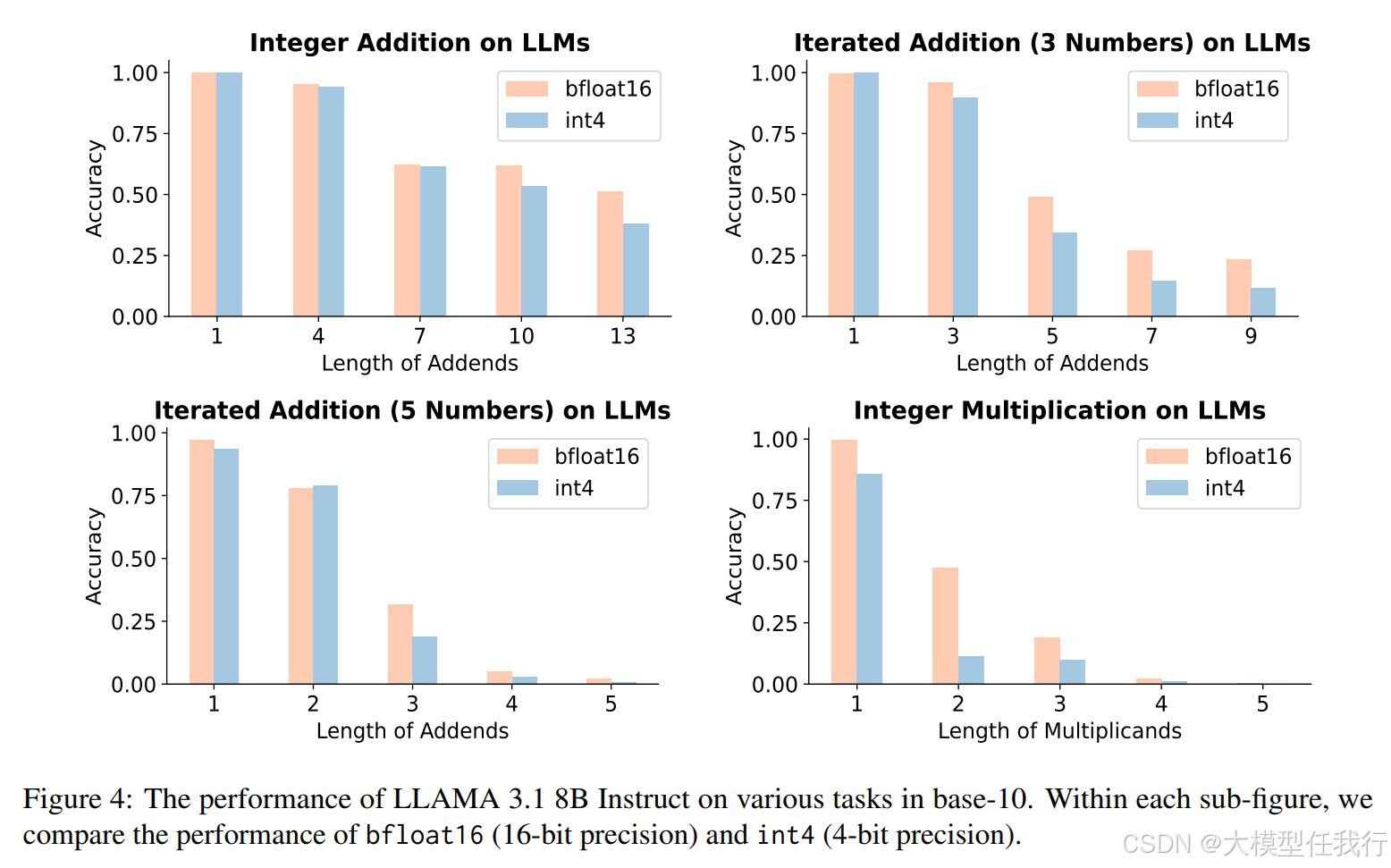
🔸低精度Transformer在处理基本算术任务时表现不佳，特别是在迭代加法和整数乘法等更复杂的任务中，性能显著下降。
🔸增加数值精度（如从int8到float32）可以显著提高Transformer模型在算术任务中的表现，减少模型大小需求。
🔸标准精度（如float32）的Transformer能够有效地解决所有基本算术任务，且模型大小需求为常数或二次方大小。
🔸低精度模型在实际应用中可能提供计算效率，但在需要精确数值推理的场景（如数学问题解决或科学计算）中可能会失败。

💡个人观点

论文通过理论证明和实验验证，揭示了数值精度在提升LLM数学推理能力中的关键作用。

附录