LeetCode高频题:最少经过几次操作可以使数组变为非降序状态
提示:本题是系列LeetCode的150道高频题,你未来遇到的互联网大厂的笔试和面试考题,基本都是从这上面改编而来的题目
互联网大厂们在公司养了一大批ACM竞赛的大佬们,吃完饭就是设计考题,然后去考应聘人员,你要做的就是学基础树结构与算法,然后打通任督二脉,以应对波云诡谲的大厂笔试面试题!
你要是不扎实学习数据结构与算法,好好动手手撕代码,锻炼解题能力,你可能会在笔试面试过程中,连题目都看不懂!比如华为,字节啥的,足够让你读不懂题
基础知识:
【1】LeetCode高频题300. 最长递增子序列
题目
作者:牛客40502855号
来源:牛客网
给定一个大小为N的无序数组arr,对数组中的每个元素可进行如下操作:
将元素移动至数组的头部
将元素移动至数组的尾部
注意:这里的移动不是通过元素的交换完成的,而是直接将元素移动到指定位置,空出来的位置由别的元素顺次填满。
问:最少经过几次操作可以使数组变为非降序状态。
一、审题
输入:
第一行输入一个正数n代表数组arr的元素个数
第二行,给出n个正整数ai,代表数组中的元素
1<=n<=3*10的5次方
1<=ai<=10的9次方
输出:
一个数ans,代表将数组操作为非降序状态所需的最小次数
比如
arr=19 7 8 25
首先8移动到首部
arr=8 19 7 25
然后将7移动到首部
7 8 19 25
2次就搞定了
了解一下最长递增子序列
19 7 8 25
最长的非递减子序列长度是3
N总长度=4
N-3=1
实际上却需要移动2次,怎么解释呢?
要不整一个范围上的尝试???
设f(i)是将i位置元素调整之后,所需要的最少操作次数
主函数调用f(0位置开始),直到i到N位置越界,看看最少调整次数是?
那么我们来讨论一波,这个f怎么写才好
(0)当i=N越界时,不需要调动,操作0次,返回0次即可
(1)任意位置i时:可以让i位置不动,算操作0次,看看f(i+1)
(2)任意位置i时:可以让i位置去首部,算操作1次,剩下的arr,看看f(i+1)
(3)任意位置i时:可以让i位置去尾部,算操作1次,剩下的arr,看看f(i+1)
这三者的答案,选择最小值返回
中间动过的arr,需要我们带着玩???
这么做可以,但是这是极其不好的尝试办法,因为arr一直变动,而且不是简单的变量类型,这种方法,蠢!
再想新的办法
据说先排序:
需要一个大小为n的数组记录排好序的结果,
然后挨个比较,统计排序数组对应原数组的下标数组,它的最长递增子序列,
最后用n减去这个序列长度
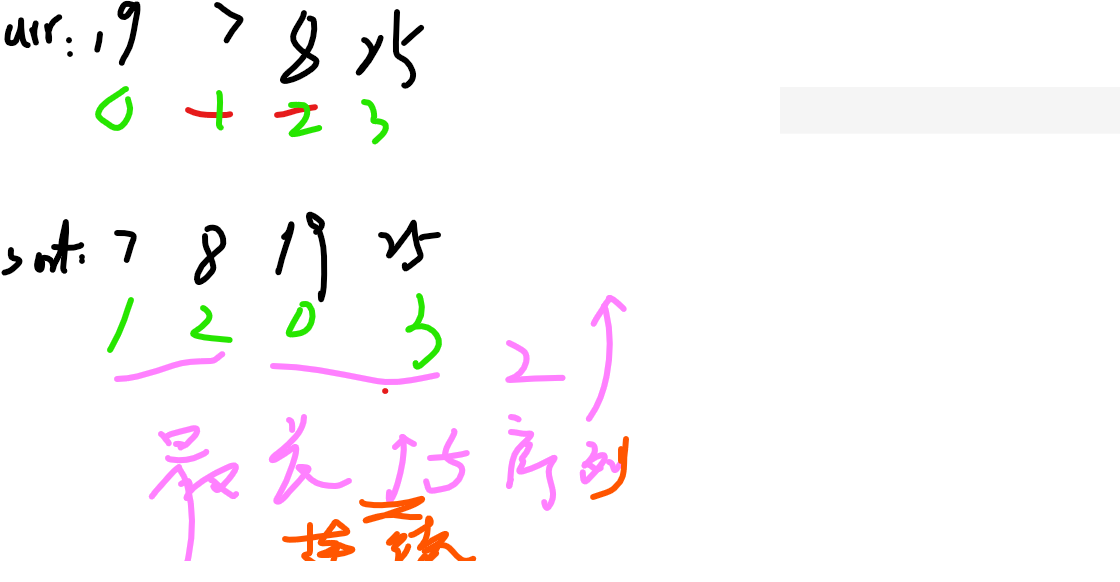
比如上面的19 7 8 25
7 8 19 25这个排序数组对应原数组的索引下标数组为
1 2 0 3,找到1203最长连续递增子数组即可
——不连续的还不行【因此我们说的基础知识【1】还不能用】
之前求过最长递增子序列的长度——这里是不连续的哦!!!【是一个贼难的题目】
【1】LeetCode高频题300. 最长递增子序列
1 2 或者0 3 构成最长连续的递增子序列,构成的2长度
故,原数组需要动几次呢?4-2=2次
没错,就是这样干
这是啥原理呢???
你最终就是想要把arr变为非递减状态,
那么原数组排序后,位置不动的最长连续递增那一堆,是我们不需要移动的位置,你想想是不是
19 7 8 25
排序后,是7 8 19 25
78 19 是动过得,但是因为19 移动到右边,然后25移动到右边就自动OK了,那么7 8是我们不需要移动的数
因此动就是要动4-2的长度
这,很难想到
OK,方法是很难想到,蔚来考的笔试题,现场3个题都很难,因此没人做出来
只能线下慢慢想,见过可能下次就会了……
我们谢谢代码!
给你一个数组arr,最长连续递增子序列的长度怎么求?
1 2 0 3
最长连续递增,既然是连续的
那就考虑以i结尾的子数组,它最长连续递增长度是多少?
实际上就是填一个表dp[i]表示以i结尾的子数组,长度是多少?
对于dp[i],只要是[i]>[i-1],dp[i]=do[i-1]+1,否则就是1
中途将最大值更新给max即可
手撕代码:
//实际上就是填一个表dp[i]表示以i结尾的子数组,长度是多少?
public static int longestConsecutiveArrLen(int[] arr){
if (arr == null || arr.length == 0) return 0;
if (arr.length == 1) return 1;
int N = arr.length;
int max = 1;//至少1
int[] dp = new int[N];//dp[i]表示以i结尾的子数组,长度是多少
//先都是1
for (int i = 0; i < N; i++) {
dp[i] = 1;//最次就是自己
}
for (int i = 1; i < N; i++) {
//从1位置看,只要是严格大于前面的位置,就算OK
dp[i] = arr[i] > arr[i - 1] ? dp[i -1] + 1 : 0;
max = Math.max(max, dp[i]);
}
return max;
}
public static void test(){
int[] arr = {1,2,0,3};
System.out.println(longestConsecutiveArrLen(arr));
}
public static void main(String[] args) {
test();
}
测试:2
问题不大,这只要是连续的就行了好说
然后我们来破解原题!
输入:
第一行输入一个正数n,代表数组arr的元素个数
第二行,给出n个正整数ai,代表数组中的元素
输出:
一个数ans,代表将数组操作为非降序状态所需的最小次数
原始数组arr,排序后为arr2
还需要用数组map记录排序后arr2对应到原始数组arr的下标位置
我们排序之后还要知道下标,就需要打包一个节点,把读进来的arri和下标i放一个节点
还要准备比较器,用arri的val排序,升序
//加装下标
public static class Node{
public int val;
public int index;//下标
public Node(int v, int i){
val = v;
index = i;
}
}
//比较器
public static class cptr implements Comparator<Node> {
@Override
public int compare(Node o1, Node o2){
return o1.val - o2.val;//升序
}
}
okay,正式手撕本题的代码:
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
int N = in.nextInt();
Node[] arr = new Node[N];
for (int i = 0; i < N; i++) {
int val = in.nextInt();
arr[i] = new Node(val, i);//包装好放入arr
}
Arrays.sort(arr, new cptr());//排序
//整一个节点装下标吧
int[] ids = new int[N];
for (int i = 0; i < N; i++) {
ids[i] = arr[i].index;//把位置搞出来,然后查最长递增子数组的长度
}
int max = longestConsecutiveArrLen(ids);
int ans = N - max;
System.out.println(ans);
}
无法就是读取arri,把arri和i包装为node
然后排序node
然后把下标ids读出来
用我们上面准备好的最长严格递增子序列的求解函数,把ids的最长递增长度求出来
然后N-max就是结果了
测试:
6
6 5 4 3 2 1
5
4
19 7 8 25
2
问题不大
整体时间复杂度在排序那o(nlog(n))
总结
提示:重要经验:
1)本题难就难在怎么想解法,你要将其变为非递减状态,原来那个数组排序后位置动过的最长递增那个子数组,是不需要动的,它的长度就是不动的长度
2)N-这个最长严格递增子序列长度就是我们要动的其他位置,难想但是见过,下次就明白了
3)另外,我们不求这个题,单独求最长递增子序列长度怎么求,那个题很经典,也很困难,要学学
3)笔试求AC,可以不考虑空间复杂度,但是面试既要考虑时间复杂度最优,也要考虑空间复杂度最优。