39. 组合总和

注意题目说明的数值分为是1 <= candidates[i] <= 200，如果出现0要单独讨论，否则会出现死循环，如果包含负数也需要单独讨论

递归函数参数：定义两个全局变量，二维数组result存放结果集，数组s存放符合条件的结果。如果是一个集合来求组合的话，就需要Index记录当前的位置，

递归终止条件：终止只有两种情况，sum大于target和sum等于target。

单层搜索的逻辑：单层for循环依然是从startIndex开始，搜索candidates集合。

出现错误：

将大于目标值的情况放到for循环中，会出现【8，7，4，3】时，当8+7>目标值11的时候就退出8，到7去选取了。

class Solution {
public:
    vector<vector<int>> res;
    vector<int> s;
    void backtracking(vector<int>& candidates, int target, int sum, int index){
        if(sum==target){
            res.push_back(s);
            return;
        }
        if(sum>target){
            return;
        }

        for(int i=index;i<candidates.size();i++){
            s.push_back(candidates[i]);
            sum+=candidates[i];
            backtracking(candidates,target,sum, i);
            sum-=candidates[i];
            s.pop_back();
        }


    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        int sum=0,index=0;
        backtracking(candidates, target, sum,index);
        return res;
    }
};

剪枝操作：

首先先对题目所给的数组进行排序，然后就可以使用前面出现错误的方法

class Solution {
public:
    vector<vector<int>> res;
    vector<int> s;
    void backtracking(vector<int>& candidates, int target, int sum, int index){
        if(sum==target){
            res.push_back(s);
            return;
        }


        for(int i=index;i<candidates.size();i++){
            s.push_back(candidates[i]);
            sum+=candidates[i];
            if(sum>target){
                sum-=candidates[i];
                s.pop_back();
                return;
            }
            backtracking(candidates,target,sum, i);
            sum-=candidates[i];
            s.pop_back();
        }


    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        res.clear();
        s.clear();
        int sum=0,index=0;
        sort(candidates.begin(),candidates.end());
        backtracking(candidates, target, sum,index);
        return res;
    }
};

40. 组合总和 II

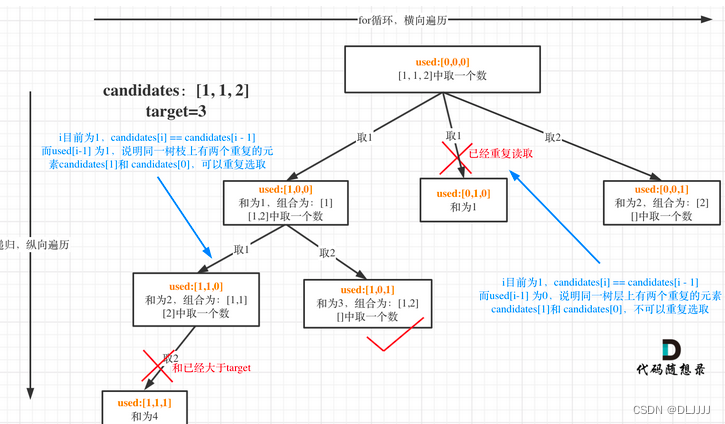
递归函数参数:此题还需要加一个bool型数组used，用来记录同一树枝上的元素是否使用过,used数组用于去重操作。

递归终止条件：终止条件为 sum == target。

单层递归逻辑：要去重的是“同一树层上的使用过”，如何判断同一树层上元素（相同的元素）是否使用过了呢。如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false，就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]。此时for循环里就应该做continue的操作。

在candidates[i] == candidates[i - 1]相同的情况下：

• used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
• used[i - 1] == false，说明同一树层candidates[i - 1]使用过

同一树层，used[i - 1] == false 才能表示，当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。而 used[i - 1] == true，说明是进入下一层递归，去下一个数，所以是树枝上，如图所示：

class Solution {
public:
    vector<int>s;
    vector<vector<int>>res;
    void backtracking(vector<int>& candidates, int target, int sum,int index,  vector<bool> used){
        if(sum==target){
            res.push_back(s);
            return;
        }
        for(int i=index;i<candidates.size()&&sum + candidates[i] <= target;i++){
            // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
            // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
            // 要对同一树层使用过的元素进行跳过
            if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
                continue;
            }
            sum+=candidates[i];
            used[i]=true;
            s.push_back(candidates[i]);
            backtracking(candidates,target,sum,i+1,used);
            s.pop_back();
            used[i]=false;
            sum-=candidates[i];
        }

    }    


    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<bool> used(candidates.size(), false);
        s.clear();
        res.clear();
        sort(candidates.begin(),candidates.end());
        backtracking(candidates,target, 0,0, used);
        return res;
    }
};

131. 分割回文串

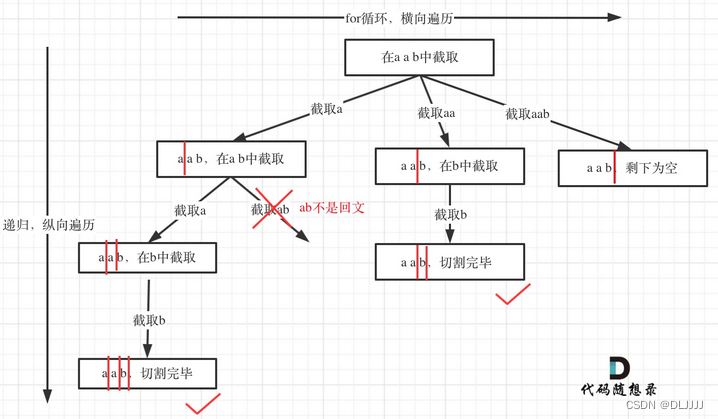
递归函数参数:全局变量数组path存放切割后回文的子串，二维数组result存放结果集。递归函数参数还需要startIndex，因为切割过的地方，不能重复切割，和组合问题也是保持一致的。

递归函数终止条件:从树形结构的图中可以看出：切割线切到了字符串最后面，说明找到了一种切割方法，此时就是本层递归的终止条件。在处理组合问题的时候，递归参数需要传入index，表示下一轮递归遍历的起始位置，这个index就是切割线。

单层搜索的逻辑:判断这个子串是不是回文，如果是回文，就加入在vector<string> path中，path用来记录切割过的回文子串。注意切割过的位置，不能重复切割，所以，backtracking(s, i + 1); 传入下一层的起始位置为i + 1。

class Solution {
public:
    vector<vector<string>> res;
    vector<string> path;
    bool isPalindrome(const string& s, int start, int end){
       while(start<end){
           if(s[start]!=s[end])return false;
           start++;
           end--;
       }
        return true;
    }
    void backtracking(string s,int index){
        if(index>=s.size()){
            res.push_back(path);
            return;
        }
        for(int i=index;i<s.size();i++){
            if(isPalindrome(s,index,i)){
                string str = s.substr(index, i - index + 1);
                path.push_back(str);
            }
            else continue;
            backtracking(s,i+1);
            path.pop_back();
        }

    }

    vector<vector<string>> partition(string s) {
        path.clear();
        res.clear();
        backtracking(s,0);
        return res;
    }
};