回溯是递归的副产品,只要有递归就会有回溯,所以回溯法也经常和二叉树遍历,深度优先搜索混在一起,因为这两种方式都是用了递归。
回溯算法能解决如下问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 棋盘问题:N皇后,解数独等等
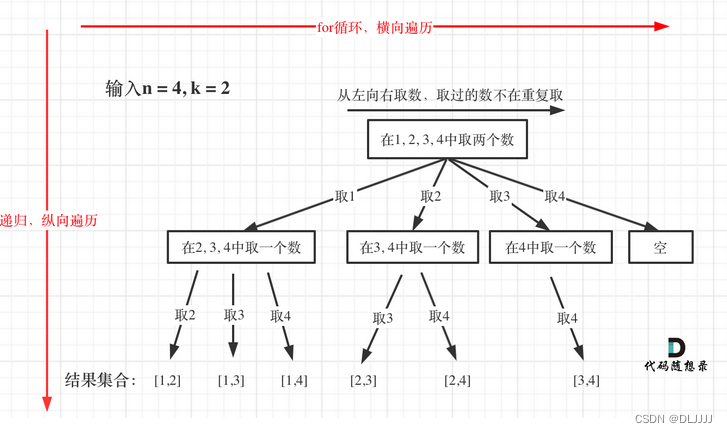
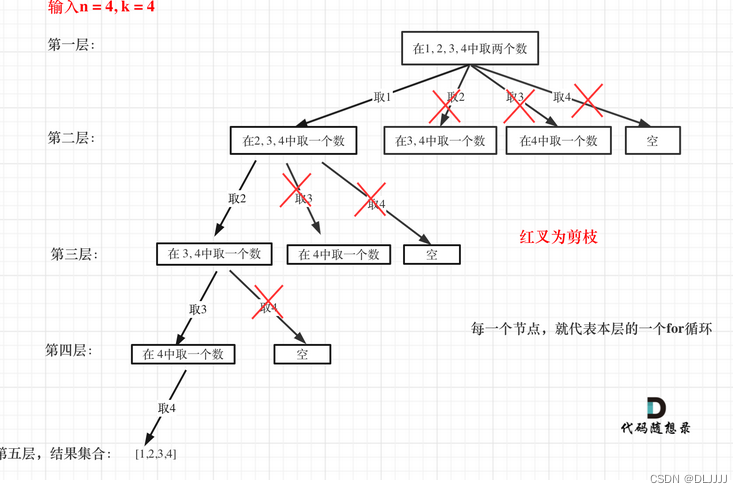
组合问题
for循环横向遍历,递归纵向遍历,回溯不断调整结果集,这个理念贯穿整个回溯法系列,剪枝操作::for循环在寻找起点的时候要有一个范围,如果这个起点到集合终止之间的元素已经不够题目要求的k个元素了,就没有必要搜索了。组合问题的终止条件常常为结果组合是否数量到了或者数值到了。
对于组合问题,一个集合来求组合的话,就需要index。如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex。
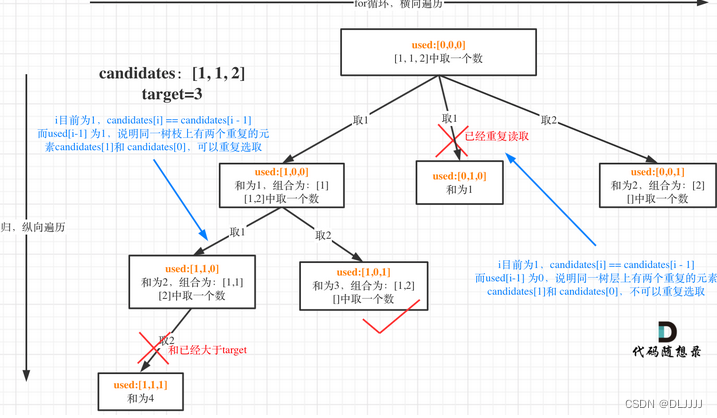
组合去重
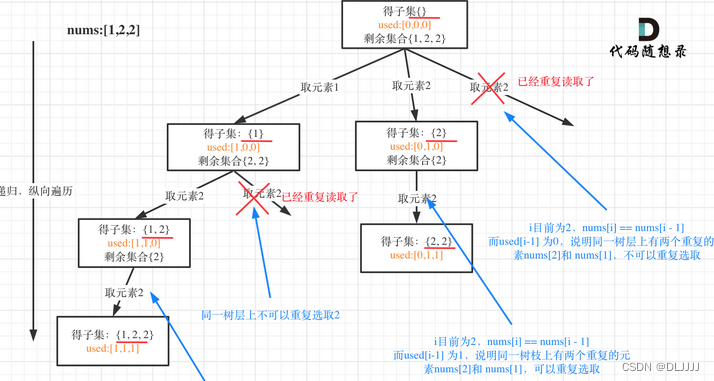
对于集合中存在的重复元素,可以理解树枝去重和树层去重。组合问题可以抽象为树形结构,那么“使用过”在这个树形结构上是有两个维度的,一个维度是同一树枝上“使用过”,一个维度是同一树层上“使用过”。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。
多个集合求组合
在现场面试的时候,要注意各种输入异常的情况,例如本题输入1 * #按键。
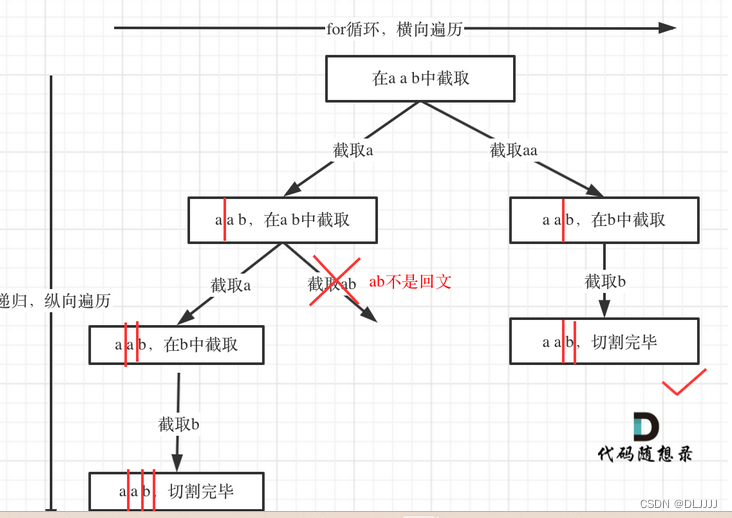
切割问题
- 切割问题其实类似组合问题
- 如何模拟那些切割线
- 切割问题中递归如何终止
- 在递归循环中如何截取子串
- 如何判断回文
但后序如何模拟切割线,如何终止,如何截取子串,其实都不好想,最后判断回文算是最简单的了。切割过的地方不能重复切割所以递归函数需要传入i + 1。
其终止条件常常为切割线(index)是否到达了数组队尾
子集问题
在树形结构中子集问题是要收集所有节点的结果,而组合问题是收集叶子节点的结果。有时,子集问题可以不用终止条件。
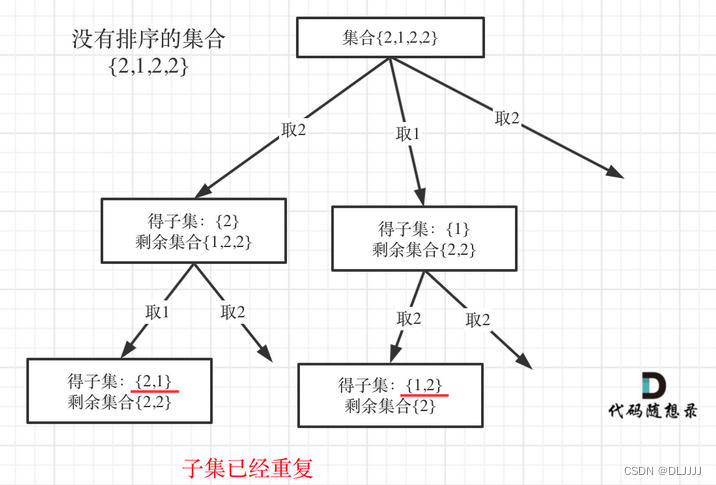
对于子集操作,有时需要使用used数组去重,使用used数组进行去重操作有一个大前提!一定要首先对集合进行排序。
子集问题一定要排序,为什么呢?对于没有排序的集合{2,1,2,2}
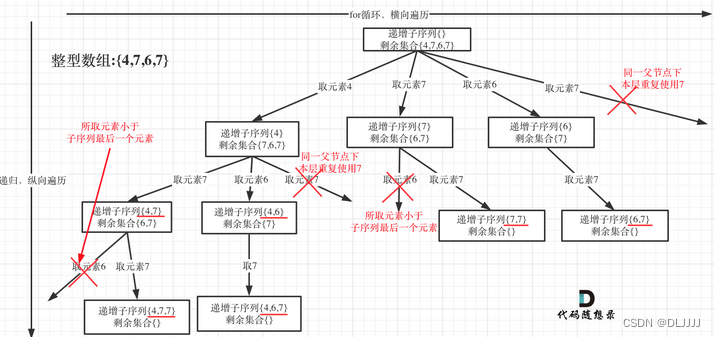
递增子序列
相对于其他的子集问题,求递增子序列不能够对集合进行排序,为了去重,会无法使用used数组,可以使用哈希表中的unordered_set进行树层去重操作
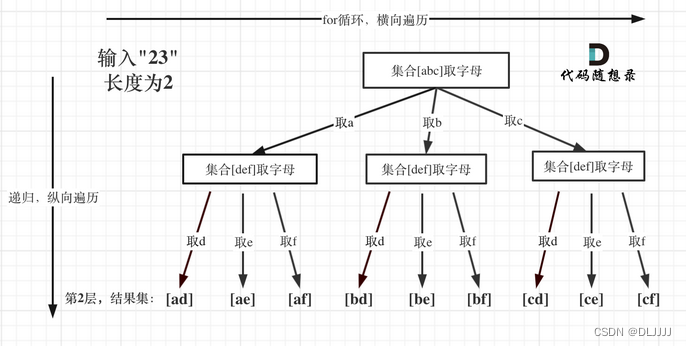
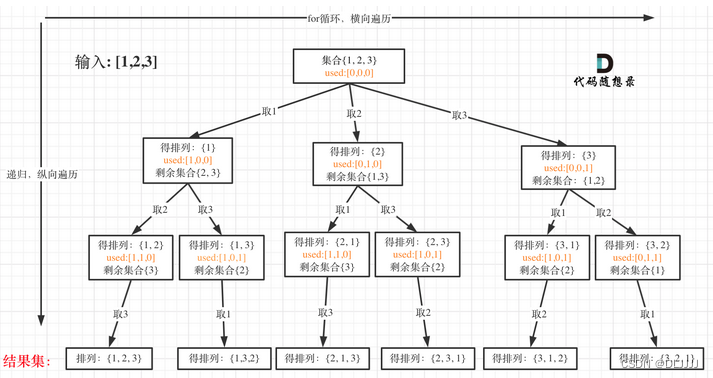
排列问题
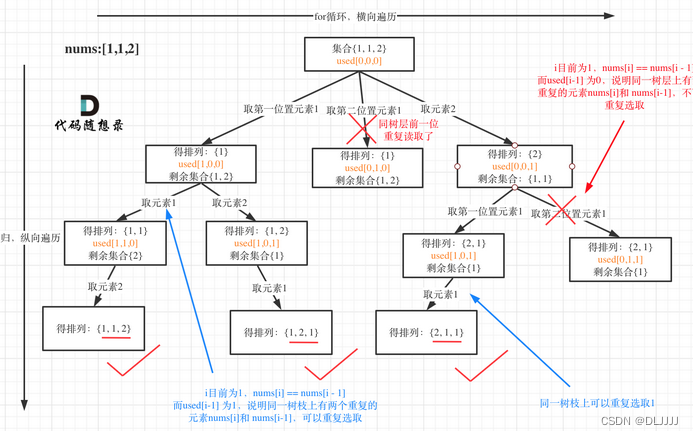
处理排列问题时,通常不需要index,但是,会存在相同元素多哦此使用的问题,此时仍然需要使用到used数组进行去重操作
对于集合中含有相同元素的排列问题,仍然使用到树枝去重和数值去重的方法