目录
LeetCode669. 修剪二叉搜索树
链接: 669. 修剪二叉搜索树 - 力扣(LeetCode)
1. 思路
常见误区
直接想法就是:递归处理,然后遇到 root.val < low 或者 root.val > high 的时候直接return NULL,一波修改,赶紧利落。
不难写出如下代码:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr || root->val < low || root->val > high) return nullptr;
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
return root;
}
};
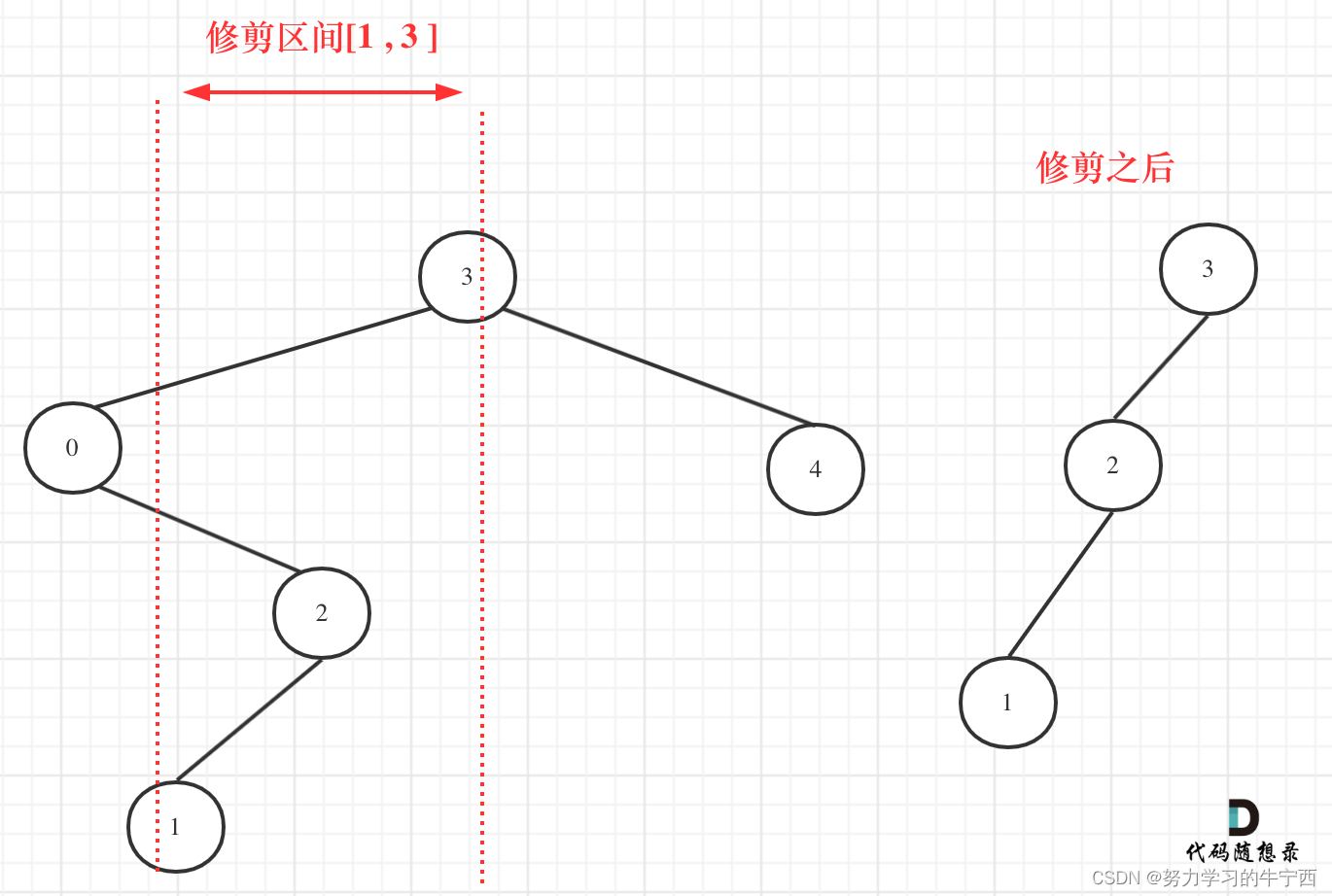
如果按照以上的代码,遍历到节点0的时候,直接返回none给3的左子树了,最后只剩下返回一个节点3;然而[1, 3]区间在二叉搜索树的中可不是单纯的节点3和左孩子节点0就决定的,还要考虑节点0的右子树;因为节点0的右子树可能会符合给的区间【1,3】;我们在重新关注一下第二个示例,如图:
所以以上的代码是不可行的!
应该怎么办?
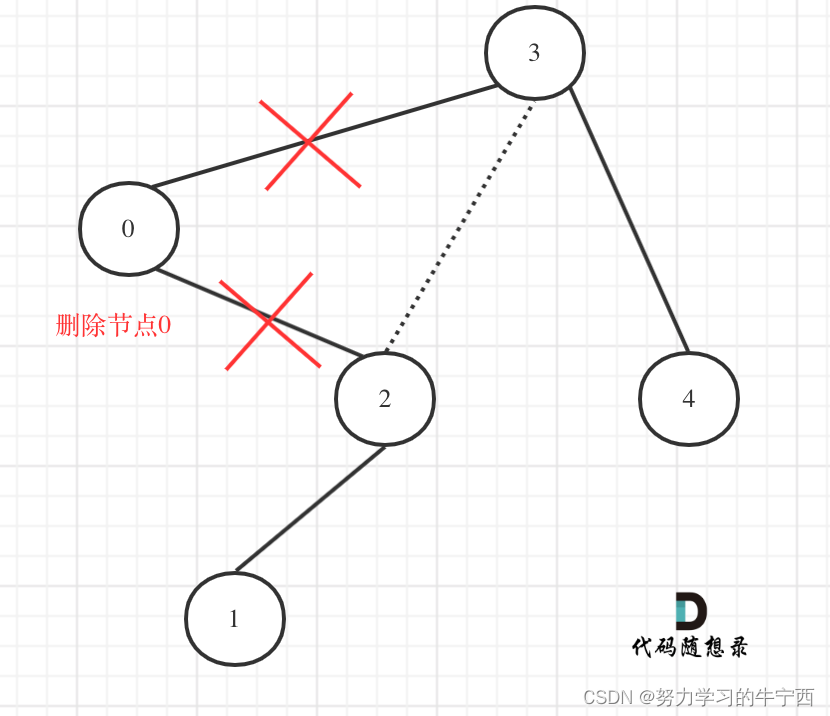
在上图中我们发现节点0并不符合区间要求,那么将节点0的右孩子 节点2 直接赋给 节点3的左孩子就可以了(就是把节点0从二叉树中移除),如图:
理解了最关键部分了,现在可以开始用递归三部曲写代码了!
2. 代码实现
-
确定递归函数的参数以及返回值
这里我们为什么需要返回值呢? 因为是要遍历整棵树,做修改,其实不需要返回值也可以,我们也可以完成修剪(其实就是从二叉树中移除节点)的操作。但是有返回值,更方便,可以通过递归函数的返回值来移除节点;
(这个点 在二叉搜索树的插入操作和二叉搜索树的删除操作中已经了解过)
class Solution: def trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode: -
确定终止条件
修剪的操作并不是在终止条件上进行的,所以就是遇到空节点返回就可以了
# Base Case if not root: return None -
确定单层递归的逻辑
- 如果root(当前节点)的元素小于low的数值,那么应该递归右子树,并返回右子树符合条件的头结点;
if root.val < low: return self.trimBST(root.right, low, high)- 如果root(当前节点)的元素大于high的,那么应该递归左子树,并返回左子树符合条件的头结点;
if high < root.val: return self.trimBST(root.left, low, high)- 接下来要将下一层处理完左子树的结果赋给root->left,处理完右子树的结果赋给root->right;最后返回root节点;
if low <= root.val <= high: root.left = self.trimBST(root.left, low, high) root.right = self.trimBST(root.right, low, high) # 返回更新后的剪枝过的当前节点root return root
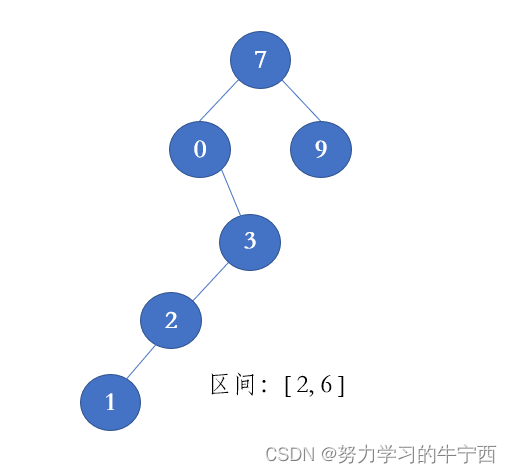
Example,模拟修剪的过程
step1. 确定新的root节点;
首先root.val = 7, 大于right=6,所以直接return root.left 节点,而节点0<2 ;所以又直接return 3 节点,现在3 在区间内了,开始处理以节点3为root的子树;
step2. 向下遍历root=3的左右子树,直接作为整个函数的root返回值;
root右子树为空,直接return None,现在开始处理以节点2为root的子树,之后这个处理的返回值,作为3节点的左子树;
step3. 继续向下遍历root= 2的左右子树,返回值为root=3节点的左右子树;
节点2在区间内,继续遍历左右子树,右子树为空直接返回None,左子树为1
step4. 向下遍历root=1的左右子树,返回值为2节点的左子树;
节点1本身就不在范围内,并且小于left=2,直接返回其右子树(为空),作为2的左子树,这样相当于删掉了节点1;
step5. 向上返回,2一个节点为root= 3的左子树,再返回3,整个树只剩3和2了,结束。
整体代码如下:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
# 递归法
# time:O(N);space:O(N)
class Solution(object):
def trimBST(self, root, low, high):
"""
:type root: TreeNode
:type low: int
:type high: int
:rtype: TreeNode
"""
# base case
if root == None: return None
# 单层递归逻辑
# 先找到合适的root
# 若当前root节点小于左界:只考虑其右子树,用于替代更新后的其本身,抛弃其左子树整体
if root.val < low: return self.trimBST(root.right,low,high)
# 若当前root节点大于右界:只考虑其左子树,用于替代更新后的其本身,抛弃其右子树整体
if root.val > high: return self.trimBST(root.left,low,high)
# 处理root的左右节点
root.left = self.trimBST(root.left,low,high)
root.right = self.trimBST(root.right,lo