本篇仍旧是MIT课程的笔记总结。首先进行消元法的展示，重点体会从矩阵A化为行最简式的过程，然后分类讨论AX = b在不同秩r下的解情况。

消元法展示

   仍旧从一个例子入手，已知矩阵A为：
$$A=\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\end{array}\right]$$

第一部分AX =0

   我们先来考虑方程$AX=0$ 的解的情况，应用初等行变换：
$$A=\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\end{array}\right]\Rightarrow \left[\begin{array}{ccc}1& 2& 3\\ 0& -3& -6\end{array}\right]\Rightarrow \left[\begin{array}{ccc}1& 2& 3\\ 0& 1& 2\end{array}\right]\Rightarrow \left[\begin{array}{ccc}1& 0& -1\\ 0& 1& 2\end{array}\right]=R$$
   我们在行最简式R矩阵中可以找到单位矩阵$I$，并可将其余部分记为$F$。关注$AX=0$，我们不难发现这样一个结果，$x_1$和$x_2$是主列所在行（也即$I$）对应的未知量，而$x_3$是自由变量，对应着$F$。如果用如下记号
$$X(pivot)=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]X(free)=\left[\begin{array}{c}{x}_3\end{array}\right]$$
   那么，对应$AX=0$的方程就可以写作：
$$\left[\begin{array}{cc}I& F\end{array}\right]\left[\begin{array}{c}X(pivot)\\ X(free)\end{array}\right]=IX(pivot)+FX(free)=0$$
   移项后就有:
$$X(pivot)=-FX(free)$$
   这在我看来是个非常优美的式子，也就是说原方程的解应该有如下的形式：
$$\begin{gathered} x_1=x_3 \\ {x}_2=-2x_3 \end{gathered}$$
   在matlab中用rref函数就得到Gauss-Jordan 消元法下的简化的行阶梯形矩阵（reduced row echelon form）。

>> A = [1,2,3;4,5,6];
>> rref(A)

ans =

     1     0    -1
     0     1     2

   也可以用solve函数验证求解的正确性。

>> syms x1;syms x2; syms x3;
>> result = solve([x1+2*x2+3*x3,4*x1+5*x2+6*x3]); % result作为struct存在
>> result.x1
 
ans =
 
x3
 
>> result.x2
 
ans =
 
-2*x3

第二部分AX =b

    我们进一步来考虑$AX=b$的情况，不如假设b列就为7和8，于是我们考虑A的增广矩阵，并应用初等行变换，即
$$\left[\begin{array}{ccccc}1& 2& 3& |& 7\\ 4& 5& 6& |& 8\end{array}\right]\Rightarrow \left[\begin{array}{ccccc}1& 2& 3& |& 7\\ 0& -3& -6& |& -20\end{array}\right]\Rightarrow \left[\begin{array}{ccccc}1& 2& 3& |& 7\\ 0& 1& 2& |& 20/3\end{array}\right]\Rightarrow \left[\begin{array}{ccccc}1& 0& -1& |& -19/3\\ 0& 1& 2& |& 20/3\end{array}\right]$$
    于是有解为
$$\begin{gathered} x_1=x_3-19/3 \\ {x}_2=-2x_3+20/3 \end{gathered}$$
    同样可以用solve函数验证其正确性

>> syms x1;syms x2; syms x3;
>> result = solve([x1+2*x2+3*x3-7,4*x1+5*x2+6*x3-8]);  % 修改求解方程
>> result.x1
 
ans =
 
x3 - 19/3
 
>> result.x2
 
ans =
 
20/3 - 2*x3

解情况讨论

    根据消元法所展示的例子，我们已经对Gauss-Jordan 消元法求解方程有了浅浅的认识，接下来我们讨论一般性的解情况，即$AX=b$ 在不同秩r下的解情况，其中A是一个$m\times n$ 的一般性矩阵。在matlab中，用rank函数就能求得矩阵的秩。

>> A = [1,2,3;4,5,6];
>> rank(A)

ans =

     2

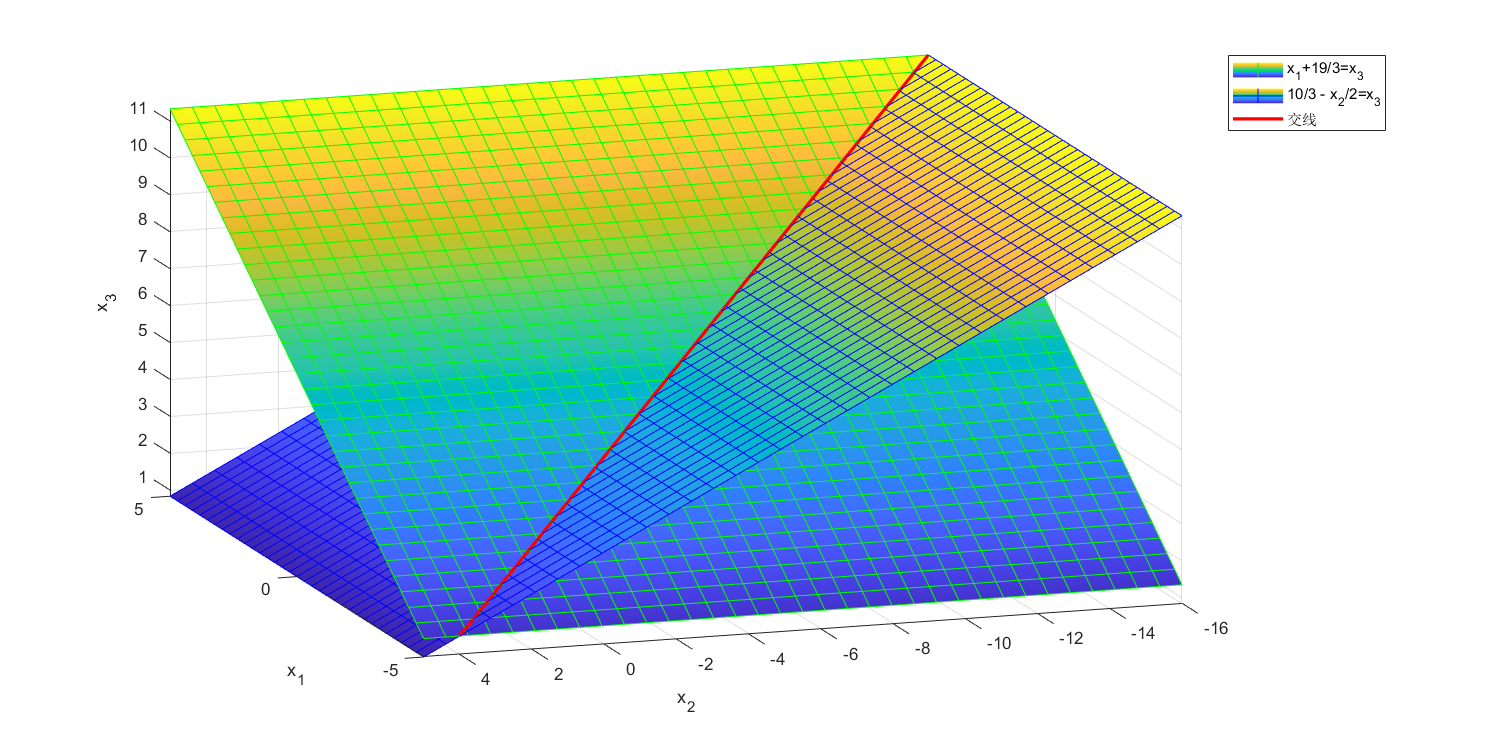
第1种情况：r = m < n

    在这种情况下，方程数小于未知数个数，必然有无穷多解。且此时由于矩阵的秩为r，所以自由向量的个数为n-r，也即说明解空间应该是一个维数为n-r的超平面。以前文所展示的例子为例，可以画出此时的解空间是一个在3维空间中的1维直线，图示和代码如下所示：

% 解空间为n-r的超平面
% 定义
syms x1; syms x2;
y1 = x1+19/3; y2 = 10/3-0.0000001*x1-0.5*x2; % 避免默认将x2读成x1
% fsurf画平面
fsurf(y1,EdgeColor='g'); hold on; fsurf(y2,EdgeColor='b'); 
% 画交线
hold on;
fplot3(x1,-2*x1-6,x1+19/3,Color = 'r',Linewidth = 2)
% 标注
legend('x_1+19/3=x_3','10/3 - x_2/2=x_3','交线');
xlabel('x_1'); ylabel('x_2');zlabel('x_3');

第2种情况：r = n < m

    实际上，再取A的转置即可研究
$$A^T=\left[\begin{array}{cc}1& 4\\ 2& 5\\ 3& 6\end{array}\right]\Rightarrow \left[\begin{array}{cc}1& 4\\ 0& -3\\ 0& -6\end{array}\right]\Rightarrow \left[\begin{array}{cc}1& 0\\ 0& 1\\ 0& 0\end{array}\right]=\left[\begin{array}{c}I\\ 0\end{array}\right]=R$$
    此时可以发现，从行去看，$R$的上部为单位阵$I$，下部为0矩阵。 此时的方程数多于未知数个数，对于右端结果项b列实则提出了要求，即要么满足为$A^T$各列的线性组合，得到一个特解；要么就无解 。比如对于下面的方程而言，就存在特解$[1,1{]}^T$：
$$\begin{gathered} x_1+4x_2=5 \\ 2x_1+5x_2=7 \\ 3x_2+6x_3=9 \end{gathered}$$
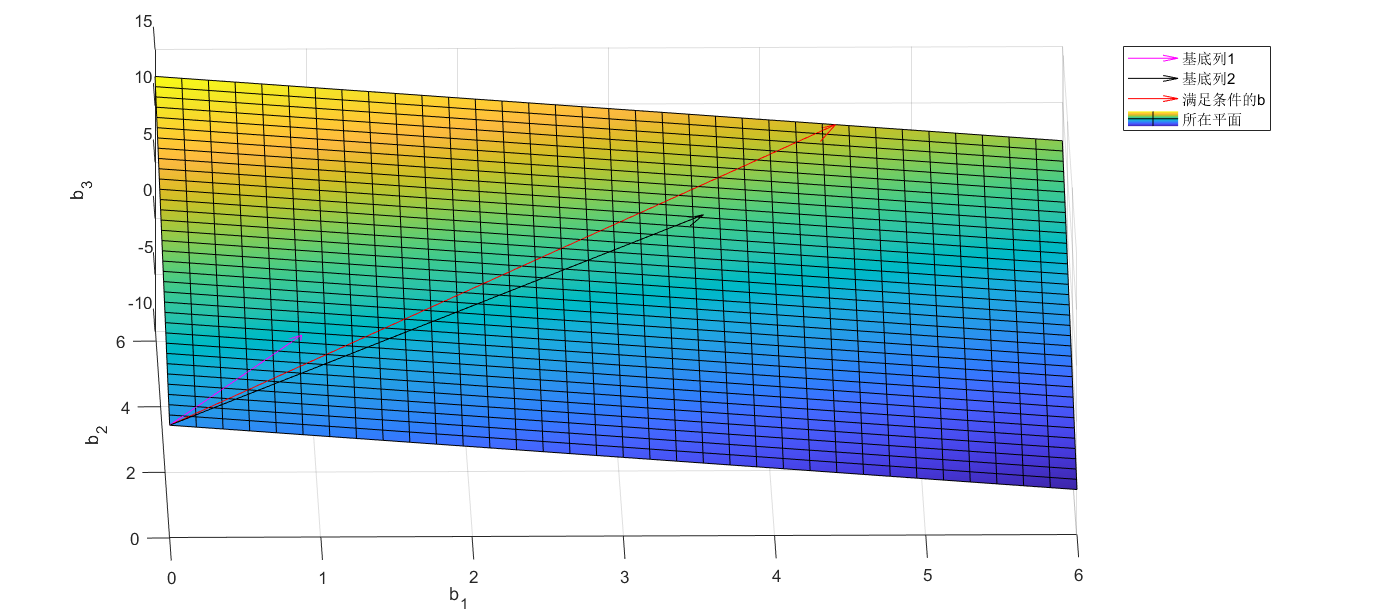
   换言之，此时b列只有是处于$A^T$所在的列空间中的某个向量才会有解。此例中，提出的要求相当于b列要位于3维空间中$A^T$所在的二维平面上。同样可以画出相应的图示，图和代码如下

% b列所在的平面

% 画向量图
quiver3(0,0,0,1,2,3,'m'); hold on; quiver3(0,0,0,4,5,6,'black'); % 基底
hold on;  quiver3(0,0,0,5,7,9,'r');  % 满足条件的b
V1 = [1;2;3]; V2 = [4;5;6];
% 求法向量
Vn = cross(V1,V2);
% 画平面
syms x1;syms x2;syms x3;
plane = -(x1*Vn(1)+x2*Vn(2))/Vn(3);
hold on;
fsurf(plane);
% 标注
legend('基底列1','基底列2','满足条件的b','所在平面');
xlabel('b_1'); ylabel('b_2'); zlabel('b_3');

第3种情况：r = n = m

   直观地看，这将是前两种情况的公共部分，于是当未知数个数与方程个数相等时，将有且仅有一个解。我们可以推导解的一般形式，由于$r=n=m$，故此时方阵可逆。对于方程两边同时左乘A的逆：
$$AX=b\Rightarrow A^{-1}AX=A^{-1}b\Rightarrow IX=A^{-1}b\Rightarrow X=A^{-1}b$$
   于是就有解的形式即为$A^{-1}b$，并可以知道此时$R$就等于单位阵$I$。也举一个例子
$$B=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]b=\left[\begin{array}{c}5\\ 6\end{array}\right]$$
   则计算结果为
$$X=B^{-1}b=\left[\begin{array}{cc}-2& 1\\ 1.5& -0.5\end{array}\right]\left[\begin{array}{c}5\\ 6\end{array}\right]=\left[\begin{array}{c}-4\\ 4.5\end{array}\right]$$
   用solve函数可验证正确性：

>> syms x1; syms x2;
>> result = solve([x1+2*x2-5,3*x1+4*x2-6]);
>> ans1 = result.x1,ans2 = result.x2
 
ans1 =
 
-4
 
 
ans2 =
 
9/2

第4种情况：r < m，r < n

    这说明了列和行都存在线性相关项，由前面的推导，我们容易得知，此时的R矩阵应有如下的形式：
$$R=\left[\begin{array}{cc}I& F\\ 0& 0\end{array}\right]$$
    当$b=0$时一定有解0，而当$b\ne 0$时则需要满足b列应在矩阵所在的列空间中。
$$\left[\begin{array}{cc}I& F\\ 0& 0\end{array}\right]\left[\begin{array}{c}X(pivot)\\ X(free)\end{array}\right]=\left[\begin{array}{c}X(pivot)+FX(free)\\ 0\end{array}\right]$$
    即此时需要满足b的$m$行中有$m-r$行是其余$r$行的线性组合时，将有解，且有无穷多解；否则将无解。当然这种有无解条件判断的表述与第2种情况中，需要b列位于矩阵所在的列空间的表述等价。
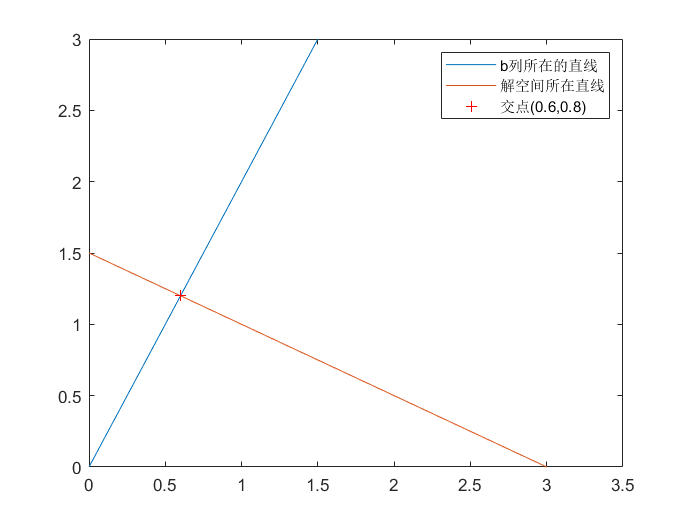
    比如修改矩阵B和对应的列b为
$$B=\left[\begin{array}{cc}1& 2\\ 2& 4\end{array}\right]b=\left[\begin{array}{c}3\\ 6\end{array}\right]$$
    此时有解，且解可为$[1,1{]}^T$,$[3,0{]}^T$，$[0,1.5{]}^T$等等，对b提出的要求可以记为是在二维平面中的1条一维直线$b_2=2b_1$,而解空间则需要满足$x_2=-0.5x_1+1.5$，容易发现这两个空间恰好是互相垂直的。对应的图片展示和代码如下：

% 解空间和b列所在空间

syms x1;
% b列所在的直线
fplot(2*x1);
% 解空间所在直线
hold on;
fplot(-x1/2+1.5);
% 标注
xlim([0,3.5]); ylim([0,3]);
% 求交点
hold on;
plot(0.6,1.2,'r+');
legend('b列所在的直线','解空间所在直线','交点(0.6,0.8)');

    最后，用一张表格梳理解的个数。