多项式轨迹
\quad
一般情况下,通过指定初始时刻
t
0
t_0
t0和终点时刻
t
1
t_1
t1 的位置、速度和加速度等条件来定义一段运动。上面的表达可用一个函数来描述:
q
=
q
(
t
)
,
t
∈
[
t
0
,
t
1
]
q=q(t), \qquad t \in [t_0,t_1]
q=q(t),t∈[t0,t1]
此函数能满足给定条件:
q
(
t
)
=
a
0
+
a
1
t
+
a
2
t
2
+
.
.
.
+
a
n
t
n
q(t)=a_0+a_1t+a_2t^2+...+a_nt^n
q(t)=a0+a1t+a2t2+...+antn
其中,根据初始时刻和终点时刻的约束条件可确定
n
+
1
n+1
n+1个
a
i
a_i
ai系数。多项式的次数
n
n
n取决于需满足条件的数量和目标运动的期望“平滑度”。由于边界条件的数量通常是偶数,所以确定的系数个数也是偶数,即多项式函数的次数
n
n
n是奇数,如3、5、7等。
\quad
通常情况下,除指定轨迹商的初始和终点时刻约束条件外,还可以指定其在某个时刻
t
f
∈
[
t
0
,
t
1
]
t_f \in [t_0,t_1]
tf∈[t0,t1]的条件,如速度、加速度和加加速度等。
三次多项式
\quad
当同时指定
t
0
t_0
t0和
t
1
t_1
t1时刻的位置和速度时,即已知
q
0
、
q
1
、
v
0
、
v
1
q_0、q_1、v_0、v_1
q0、q1、v0、v1时,轨迹需要满足四个约束条件,即可以采用三次多项式来表示轨迹:
q
(
t
)
=
a
0
+
a
1
(
t
−
t
0
)
+
a
2
(
t
−
t
0
)
2
+
a
3
(
t
−
t
0
)
3
t
0
≤
t
≤
t
1
q(t)=a_0+a_1(t-t_0)+a_2(t-t_0)^2+a_3(t-t_0)^3 \qquad t_0 \leq t \leq t_1
q(t)=a0+a1(t−t0)+a2(t−t0)2+a3(t−t0)3t0≤t≤t1
将上述约束条件代入,即有:
{
q
(
t
0
)
=
q
0
q
(
t
1
)
=
q
1
q
˙
(
t
0
)
=
v
0
q
˙
(
t
1
)
=
v
1
\left\{ \begin{aligned} q(t_0) & = & q_0 \\ q(t_1) & = & q_1 \\ \dot{q}(t_0) & = & v_0 \\ \dot{q}(t_1) & = & v_1 \end{aligned} \right.
⎩
⎨
⎧q(t0)q(t1)q˙(t0)q˙(t1)====q0q1v0v1
可解得系数的值:
{
a
0
=
q
0
a
1
=
v
0
a
2
=
3
h
−
(
2
v
0
+
v
1
)
T
T
2
a
3
=
−
2
h
+
(
v
0
+
v
1
)
T
T
3
\left\{ \begin{aligned} a_0 & = q_0 \\ a_1 & = v_0 \\ a_2 & = \frac{3h-(2v_0+v_1)T}{T^2}\\ a_3 & = \frac{-2h+(v_0+v_1)T}{T^3} \end{aligned} \right.
⎩
⎨
⎧a0a1a2a3=q0=v0=T23h−(2v0+v1)T=T3−2h+(v0+v1)T
其中:
h
=
q
1
−
q
0
,
T
=
t
1
−
t
0
h=q_1-q_0,T=t_1-t_0
h=q1−q0,T=t1−t0。
\quad
基于上述结论可获得通过
n
n
n个点序列并具有连续速度的轨迹。整段轨迹可分为
n
−
1
n-1
n−1段,每一段在
t
k
t_k
tk和
t
k
+
1
t_{k+1}
tk+1时刻通过位置点
q
k
q_k
qk和
q
k
+
1
q_{k+1}
qk+1,并且速度分别为
v
k
v_k
vk和
v
k
+
1
v_{k+1}
vk+1。上述式子用于定义每一段中
4
(
n
−
1
)
4(n-1)
4(n−1)个参数
a
0
k
、
a
1
k
a_{0k}、a_{1k}
a0k、a1k、
a
2
k
、
a
3
k
a_{2k}、a_{3k}
a2k、a3k。
三次多项式轨迹代码实现(Matlab)
clc;
clear all;
t = [0, 2, 4, 8, 10];
q = [10, 20, 0, 30, 40];
v = [0, -10, 10, 3, 0];
cubic_trajectory(t, q, v);
function cubic_trajectory(t, q, v)
% t: 时间点数组
% q: 对应的位移点数组
% v: 对应的速度点数组
n = length(t) - 1; % 轨迹段数
a = zeros(n, 4); % 每一段的四个系数
h = q(2:end) - q(1:end-1);
T = t(2:end) - t(1:end-1);
for k = 1:n
a(k, 1) = q(k);
a(k, 2) = v(k);
a(k, 3) = (3*h(k) - (2*v(k) + v(k+1))*T(k)) / T(k)^2;
a(k, 4) = (-2*h(k) + (v(k) + v(k+1))*T(k)) / T(k)^3;
end
% 插值和绘图
t_plot = linspace(t(1), t(end), 1000);
q_plot = zeros(size(t_plot));
v_plot = zeros(size(t_plot));
a_plot = zeros(size(t_plot));
for i = 1:length(t_plot)
for k = 1:n
if t_plot(i) >= t(k) && t_plot(i) <= t(k+1)
tau = t_plot(i) - t(k);
q_plot(i) = a(k, 1) + a(k, 2)*tau + a(k, 3)*tau^2 + a(k, 4)*tau^3;
v_plot(i) = a(k, 2) + 2*a(k, 3)*tau + 3*a(k, 4)*tau^2;
a_plot(i) = 2*a(k, 3) + 6*a(k, 4)*tau;
break;
end
end
end
% 计算每个时间点的q, v, a
q_points = zeros(size(t));
v_points = zeros(size(t));
a_points = zeros(size(t));
q_points(1) = a(1, 1) + a(1, 2)*t(1) + a(1, 3)*t(1)^2 + a(1, 4)*t(1)^3;
v_points(1) = a(1, 2) + 2*a(1, 3)*t(1) + 3*a(1, 4)*t(1)^2;
a_points(1) = 2*a(1, 3) + 6*a(1, 4)*t(1);
for k = 2:n
tau = t(k) - t(k-1);
q_points(k) = a(k-1, 1) + a(k-1, 2)*tau + a(k-1, 3)*tau^2 + a(k-1, 4)*tau^3;
v_points(k) = a(k-1, 2) + 2*a(k-1, 3)*tau + 3*a(k-1, 4)*tau^2;
a_points(k) = 2*a(k-1, 3) + 6*a(k-1, 4)*tau;
end
q_points(end) = q(end);
v_points(end) = v(end);
a_points(end) = 2*a(n, 3) + 6*a(n, 4)*(t(end)-t(end-1));
figure;
subplot(3,1,1);
plot(t_plot, q_plot, 'LineWidth', 1.5);
hold on;
plot(t, q_points, 'o', 'MarkerEdgeColor', 'r', 'MarkerFaceColor', 'none');
xlabel('时间 (s)');
ylabel('位置 (m)');
title('位置-时间图');
hold off;
subplot(3,1,2);
plot(t_plot, v_plot, 'LineWidth', 1.5);
hold on;
plot(t, v_points, 'o', 'MarkerEdgeColor', 'r', 'MarkerFaceColor', 'none');
xlabel('时间 (s)');
ylabel('速度 (m/s)');
title('速度-时间图');
hold off;
subplot(3,1,3);
plot(t_plot, a_plot, 'LineWidth', 1.5);
hold on;
plot(t, a_points, 'o', 'MarkerEdgeColor', 'r', 'MarkerFaceColor', 'none');
xlabel('时间 (s)');
ylabel('加速度 (m/s^2)');
title('加速度-时间图');
hold off;
end
结果
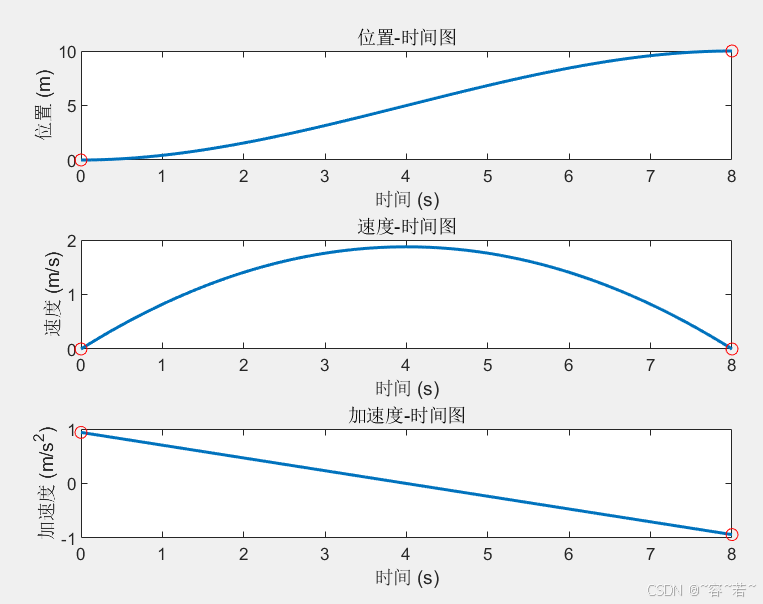
- 当输入为: q 0 = 0 、 q 1 = 10 、 t 0 = 0 、 t 1 = 8 、 v 0 = v 1 = 0 q_0=0、q_1=10、t_0=0、t_1=8、v_0=v_1=0 q0=0、q1=10、t0=0、t1=8、v0=v1=0, 即
t = [0, 8];
q = [0, 10];
v = [0, 0];
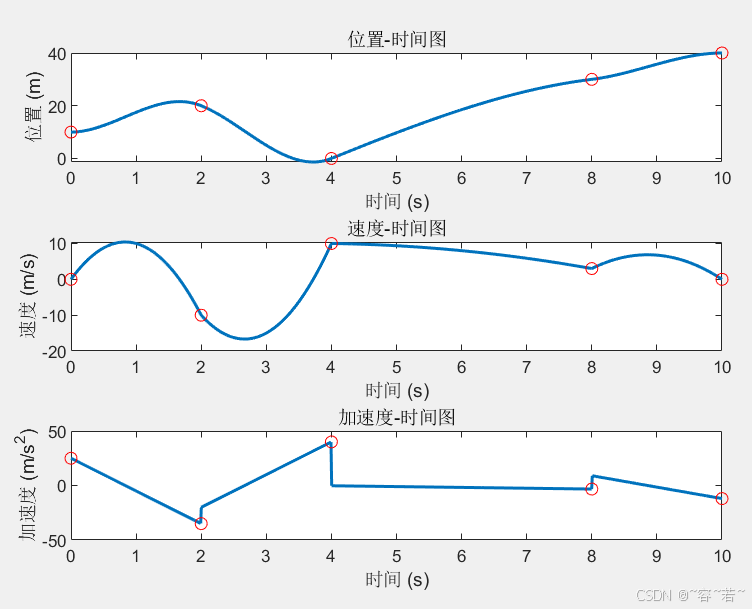
2. 当输入为多点轨迹时间、位置、速度时:
t
0
=
0
,
t
1
=
2
,
t
2
=
4
,
t
3
=
8
,
t
4
=
10
,
q
0
=
10
,
q
1
=
20
,
q
2
=
0
,
q
3
=
30
,
q
4
=
40
,
v
0
=
0
,
v
1
=
−
10
,
v
2
=
10
,
v
3
=
3
,
v
4
=
0
t_0=0,\quad t_1=2,\quad t_2=4,\quad t_3=8,\quad t_4=10,\\ q_0=10,\quad q_1=20,\quad q_2=0,\quad q_3=30, \quad q_4=40 ,\\ v_0=0,\quad v_1=-10,\quad v_2=10,\quad v_3=3,\quad v_4=0
t0=0,t1=2,t2=4,t3=8,t4=10,q0=10,q1=20,q2=0,q3=30,q4=40,v0=0,v1=−10,v2=10,v3=3,v4=0
即输入为:
t = [0, 2, 4, 8, 10];
q = [10, 20, 0, 30, 40];
v = [0, -10, 10, 3, 0];