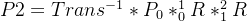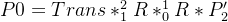1.概念定义
1.1 世界坐标系与描述坐标系
世界坐标系
笛卡尔几何空间中用以确定几何空间位置的描述坐标架。通俗易懂的讲,就是所建立的符合右手笛卡尔定则的空间坐标系,也称为基础坐标系、原坐标系或世界坐标系。
描述坐标系
顾名思义,描述坐标系是在基础坐标系的基础上建立的用以描述物体空间位置关系的坐标系,其相对于基础坐标系以一定姿态存在。由于在世界坐标系中一些空间运动关系极其复杂,但在描述坐标系中却能简单描述,所以在描述坐标系中进行建模会使计算更加简单。
1.2 坐标系间的空间位姿变换
世界坐标系是固定不变的,描述坐标系以一定姿态存在于世界坐标系中。描述坐标系可以经初始时与描述坐标系重合的坐标系经过旋转和平移变换得到,称为坐标系间的空间位姿变换。其变换方法有两种,第一种为固定变换,另一种为欧拉变换。
固定变换
如图所示,世界坐标系为 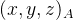
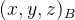
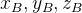
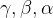
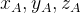
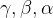
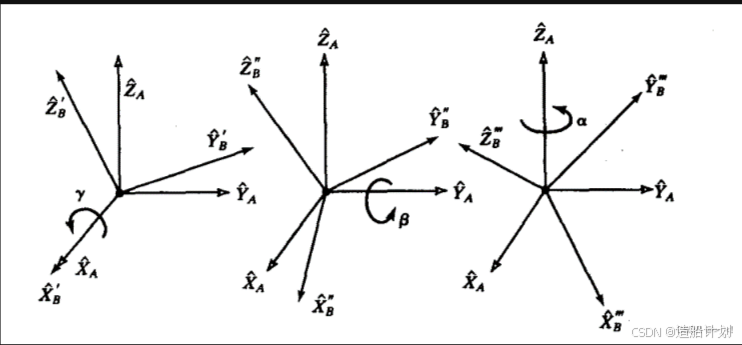
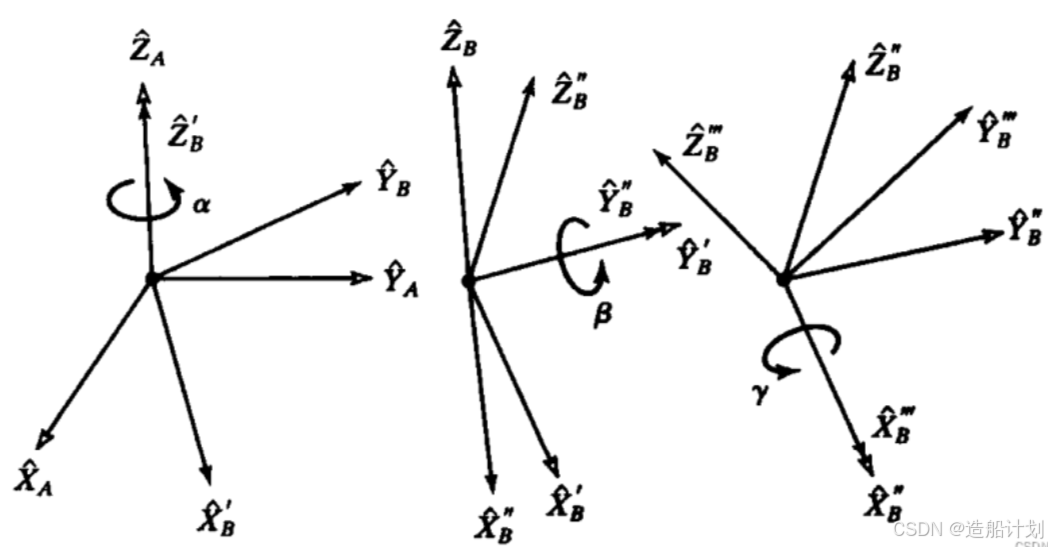
欧拉变换
在欧拉变换中,使描述坐标系绕 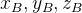
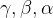
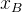
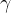
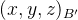
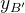
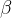
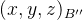
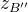
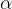
2. 固定旋转和欧拉旋转的计算形式
假设初始时描述坐标系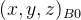
描述坐标系先绕 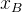
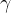
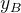
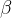
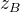
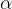
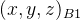
固定旋转
固定旋转为将坐标轴矢量按照先后顺序左乘旋转矩阵,其数学描述为:
欧拉旋转
欧拉旋转为将坐标轴矢量按照先后顺序右乘旋转矩阵,其数学描述为:
值得注意的是,旋转矩阵的逆等于旋转矩阵的转置。对向量右乘旋转矩阵几何意义为绕坐标系进行反向旋转,方向为右手定则反向。欧拉变换的本质就是将需要空间变换的矢量每次旋转都在基础坐标系下表示,然后再按定轴旋转方式旋转,从而实现动坐标系的空间旋转。
3. 空间坐标系间的坐标变换方式
假设初始时描述坐标系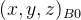
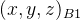
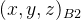
![P _0= [a \ b \ c \ 1 ]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9QJTIwXzAlM0QlMjAlNUJhJTIwJTVDJTIwYiUyMCU1QyUyMGMlMjAlNUMlMjAxJTIwJTVE)
假设坐标系2中坐标矢量![P _2= [a \ b \ c \ 1 ]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9QJTIwXzIlM0QlMjAlNUJhJTIwJTVDJTIwYiUyMCU1QyUyMGMlMjAlNUMlMjAxJTIwJTVE)
这里需要强调的是左乘平移矩阵的逆等价于将向量按平移矩阵的相反方向进行平移,不存在右乘平移矩阵。
以上内容均为本人近期学习心得,或许有错误之处,欢迎交流~
如需matlab验证代码的欢迎评论呦~
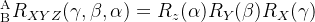
![x=[1\ 0\ 0\ 1]\\ y=[0\ 1\ 0\ 1]\\ z=[0\ 0\ 1\ 1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT94JTNEJTVCMSU1QyUyMDAlNUMlMjAwJTVDJTIwMSU1RCU1QyU1QyUyMHklM0QlNUIwJTVDJTIwMSU1QyUyMDAlNUMlMjAxJTVEJTVDJTVDJTIweiUzRCU1QjAlNUMlMjAwJTVDJTIwMSU1QyUyMDElNUQ%3D)
![x=Rov(z,\alpha)Rov(y,\beta)Rov(x,\gamma)[1\ 0\ 0\ 1]'\\ y=Rov(z,\alpha)Rov(y,\beta)Rov(x,\gamma)[0\ 1\ 0\ 1]'\\ z=Rov(z,\alpha)Rov(y,\beta)Rov(x,\gamma)[0\ 0\ 1\ 1]'](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT94JTNEUm92JTI4eiUyQyU1Q2FscGhhJTI5Um92JTI4eSUyQyU1Q2JldGElMjlSb3YlMjh4JTJDJTVDZ2FtbWElMjklNUIxJTVDJTIwMCU1QyUyMDAlNUMlMjAxJTVEJTI3JTVDJTVDJTIweSUzRFJvdiUyOHolMkMlNUNhbHBoYSUyOVJvdiUyOHklMkMlNUNiZXRhJTI5Um92JTI4eCUyQyU1Q2dhbW1hJTI5JTVCMCU1QyUyMDElNUMlMjAwJTVDJTIwMSU1RCUyNyU1QyU1QyUyMHolM0RSb3YlMjh6JTJDJTVDYWxwaGElMjlSb3YlMjh5JTJDJTVDYmV0YSUyOVJvdiUyOHglMkMlNUNnYW1tYSUyOSU1QjAlNUMlMjAwJTVDJTIwMSU1QyUyMDElNUQlMjc%3D)
![x=[1\ 0\ 0\ 1]Rov(x,\gamma)Rov(y,\beta)Rov(z,\alpha)\\ y=[0\ 1\ 0\ 1]Rov(x,\gamma)Rov(y,\beta)Rov(z,\alpha)\\ z=[0\ 0\ 1\ 1]Rov(x,\gamma)Rov(y,\beta)Rov(z,\alpha)](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT94JTNEJTVCMSU1QyUyMDAlNUMlMjAwJTVDJTIwMSU1RFJvdiUyOHglMkMlNUNnYW1tYSUyOVJvdiUyOHklMkMlNUNiZXRhJTI5Um92JTI4eiUyQyU1Q2FscGhhJTI5JTVDJTVDJTIweSUzRCU1QjAlNUMlMjAxJTVDJTIwMCU1QyUyMDElNURSb3YlMjh4JTJDJTVDZ2FtbWElMjlSb3YlMjh5JTJDJTVDYmV0YSUyOVJvdiUyOHolMkMlNUNhbHBoYSUyOSU1QyU1QyUyMHolM0QlNUIwJTVDJTIwMCU1QyUyMDElNUMlMjAxJTVEUm92JTI4eCUyQyU1Q2dhbW1hJTI5Um92JTI4eSUyQyU1Q2JldGElMjlSb3YlMjh6JTJDJTVDYWxwaGElMjk%3D)