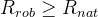本文将对抗样本的预测误差分解为自然误差和边界误差的综合,利用分类校准损失理论提供了一个可微的上界。该上界时所有概率分布和可测量预测量的最紧的可能上界。同时设计出了一种新的防御方法:TRADES,用来抵消对抗稳健性和准确性。
主要贡献
1)理论上,通过将鲁棒误差分解为自然误差和边界误差之和,来描述分类问题的准确性和鲁棒性之间的权衡。利用了分类校准损失理论,给出了这两个项的可微上界,证明了它是所有概率分布和可测预测因子上最严格的一致上界。
2)算法上,受理论的分析的启发提出了一种新的对抗性防御形式,即TRADES,作为优化正则化替代损失。损失由两项组成:经验风险最小化项鼓励算法最大化自然精度,而正则化项鼓励算法将决策边界推离数据,以提高对抗鲁棒性
符号说明
粗体大写字母表示随机向量,粗体小写字母表示随机向量的实现,大写字母表示随机变量,小写字母表示随机变量的实现。
前言
误差
有界
自然分类误差:
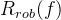
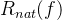
边界误差:
在实际中,想要最优化0-1 loss是很困难的,往往用替代的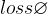
在自然误差和边界误差中都涉及到了0-1损失函数,本文的目标是设计这两个向的紧可微上界,为了实现这一目标,利用了分类校准损失理论。
classification-calibrated surrogate loss
分类校准损失,对于![\eta \in [0,1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNldGElMjAlNUNpbiUyMCU1QjAlMkMxJTVE)
假设1(分类校准损失):假设替代损失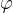
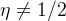
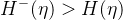
该假设对于分类问题是不可缺少的,因为没有它,贝叶斯最优分类器就不能是风险的最小化者。
性质;
(最后一句话的意思是描述了替代损失与非分类校准损失的接近程度)
引理2.1:在假设1 的条件下,函数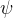

通过这个标定的损失函数的性质,可以推得优化函数的上界。
Relating 0-1 loss to surrogate loss
上界
定理3.1:
在假设1的条件下,对于任何非负损失函数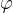
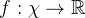
![\chi \times {}{[\pm 1}]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNjaGklMjAlNUN0aW1lcyUyMCU3QiU3RCU3QiU1QiU1Q3BtJTIwMSU3RCU1RA%3D%3D)
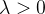
对抗样本存在的正式理由:学习模型容易受到小型对抗攻击,因为数据位于模型决策边界附近的概率比较大,故小扰动可能会将数据点移动到决策边界的错误一侧,导致分类模型的鲁棒性较弱。
下界
定理3.2:假设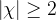
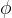

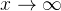
![\xi >0,\theta \in [0,1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUN4aSUyMCUzRTAlMkMlNUN0aGV0YSUyMCU1Q2luJTIwJTVCMCUyQzElNUQ%3D)
![\chi \times {}{[\pm 1}]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNjaGklMjAlNUN0aW1lcyUyMCU3QiU3RCU3QiU1QiU1Q3BtJTIwMSU3RCU1RA%3D%3D)
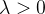

定理3.2证明了在损失函数存在额外条件的情况下,定理3.1中上界很紧。
算法
优化:
定理3.1和3.2阐明了对抗性防御算法设计,为了最小化
(3)捕捉了自然错误和鲁棒错误之间的权衡:(3)中的第一项通过最小化f (X)和Y之间的“差”来优化自然错误,而第二项正则化则通过最小化自然例子f (X)和对抗性例子f (X0)的预测的“差”来促进输出的平滑,即通过最小化自然例子f (X)和对抗性例子f (X0)的预测的“差”来推动分类器的决策边界远离样本实例。