17.电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = ""
输出:[]
示例 3:
输入:digits = "2"
输出:["a","b","c"]
提示:
0 <= digits.length <= 4digits[i]是范围['2', '9']的一个数字。
该题其实考察的是深度优先遍历
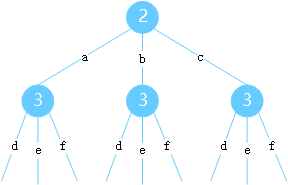
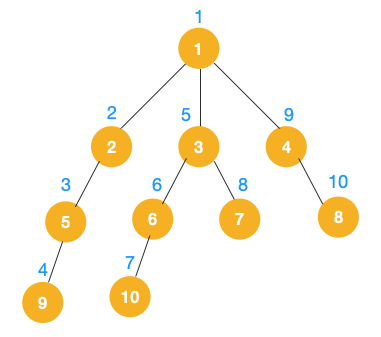
什么是树的深度优先遍历,下图举例?
-
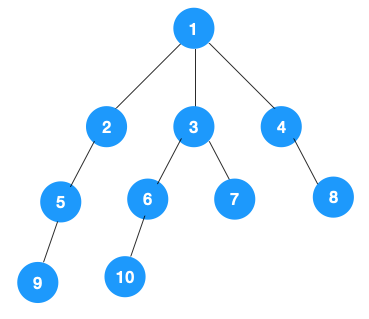
我们从根节点 1 开始遍历,它相邻的节点有 2,3,4,先遍历节点 2,再遍历 2 的子节点 5,然后再遍历 5 的子节点 9。
-
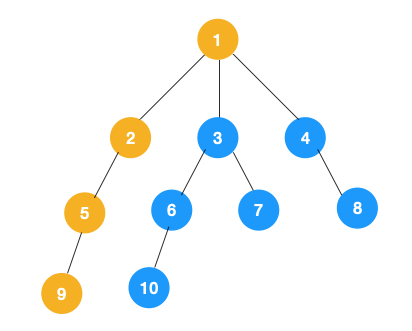
上图中一条路已经走到底了(9是叶子节点,再无可遍历的节点),此时就从 9 回退到上一个节点 5,看下节点 5 是否还有除 9 以外的节点,没有继续回退到 2,2 也没有除 5 以外的节点,回退到 1,1 有除 2 以外的节点 3,所以从节点 3 开始进行深度优先遍历,如下:
-
同理从 10 开始往上回溯到 6, 6 没有除 10 以外的子节点,再往上回溯,发现 3 有除 6 以外的子点 7,所以此时会遍历 7。
-
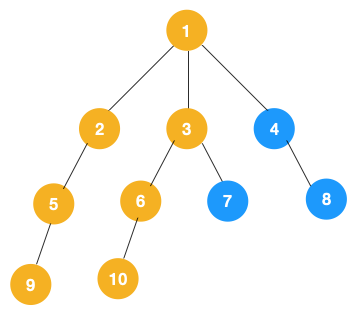
从 7 往上回溯到 3, 1,发现 1 还有节点 4 未遍历,所以此时沿着 4, 8 进行遍历,这样就遍历完成了。
完整的节点的遍历顺序如下(节点上的的蓝色数字代表):
以上的遍历不难发现这就是树的前序遍历,实际上不管是前序遍历,还是中序遍历,亦或是后序遍历,都属于深度优先遍历。并且深度优先遍历有递归和非递归两种表现形式
回归本题,代码使用递归:
public class Problem_0017_LetterCombinationsOfAPhoneNumber {
public static char[][] phone = {
{},
{},
{'a', 'b', 'c'},
{'d', 'e', 'f'},
{'g', 'h', 'i'},
{'j', 'k', 'l'},
{'m', 'n', 'o'},
{'p', 'q', 'r', 's'},
{'t', 'u', 'v'},
{'w', 'x', 'y', 'z'}
};
public List<String> letterCombinations(String digits) {
List<String> ans = new ArrayList<>();
if (digits == null || digits.length() == 0) {
return ans;
}
char[] str = digits.toCharArray();
char[] path = new char[str.length];
process(str, 0, path, ans);
return ans;
}
// str表示按的哪些键['2','3']
// 按出的结果是什么都在path里,比如【'a','d'】,【'a','e'】.....
// str[index...] 按完之后,有哪些组合,放入到ans里,index用来记录当前按到了哪一位
public static void process(char[] str, int index, char[] path, List<String> ans) {
if (index == str.length) {
ans.add(String.valueOf(path));
} else {
char[] cands = phone[str[index] - '0'];
for (char cur : cands) {
path[index] = cur;
process(str, index + 1, path, ans);
}
}
}
}