基础算法(一） 纯干货！！ 排序及二分算法

码了7天，手残党也能看懂！！
手残第一篇：第一章 基础算法（一）

提示：你的三连是作者输出下去的动力哦！！真的真的！！！（小声哔哔：赶紧收藏！！内容持续更新中。。。）

前言

• 已经断更一周了，深感愧疚！突然在思考一个问题！

是衣服穿得少比较冷还是裤子穿得少比较冷？我这衣服穿三件却没穿秋裤的老年人冷的直哆嗦。

• 哈哈哈哈废话不多说，以下是我学习算法的一些心得笔记，全是模板干货，感谢各位大佬，小伙伴的支持。以后一周一更，希望对各位有所帮助，话不多说直接上干货！！

不懂的问题欢迎下方评论区留言哦，一定一定尽量回答

一、排序

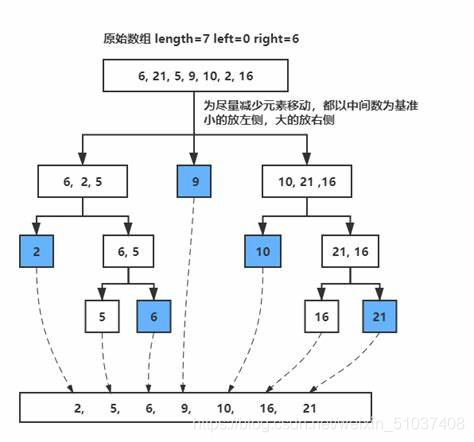
1.快速排序 quick_sort

• 快速排序由于排序效率在同为O(N*logN)的几种排序方法中效率较高，因此经常被采用，再加上快速排序思想----分治法也确实实用，因此很多软件公司的笔试面试，包括像腾讯，微软等知名IT公司都喜欢考这个，还有大大小的程序方面的考试如软考，考研中也常常出现快速排序的身影。
• 下面是作者自己总结的想法，帮助大家快速理解： 原理：首先定义一个基准值(为了防止边界问题，这里推荐取中点x)，以及指针 i ,p。指针i为起始位小于基准值向右移，指针p为终点位大于基准向左移，不符条件时指针停止，两指针进行交换（即swap），进行下次循环重新定义基点，最终变成有序序列。

图解如下：

代码如下（示例）：

void quick_sort(int q[],int i,int p)
{
	if(i>=p) return;
	int x =(i+p)<<1,g=i-1,u=p+1;
	while(i<p)
	{
		do g++ ; while(q[g]<x);
		do u--; while(q[u]>x);
		if(i<j)	swap(q[g],[u]);
	
		quick_sort(q,i,g),quick_sort(q,g+1,p);
	}
}

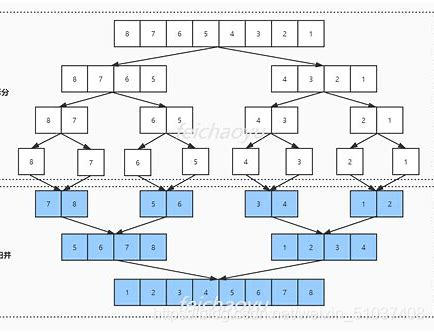
2.归并排序 merge_sort

• 归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and
  Conquer）的一个非常典型的应用。时间复杂度同为O(N*logN)。许多小伙伴一眼看去肯定是懵的吧（和我当初一样哈哈哈，苦逼专研4小时），先将经验总结如下：
• 原理：将数组以递归的方式分为n个元素即时间复杂度为logN，再进行整合（此过程也是在递归的过程中完成）此过程时间复杂度为n，整合的过程中比较，因此就完成了归并排序。主要思想还是先分后合，可以看着代码将思想代入无限递归的最后一层，会帮助你清晰很多！

图解如下：

代码如下（示例）：

void merge_sort(int q[],int i,int p)
{
	if(i>=p) return;
	int mid = (i+p)>>1;
	merge_sort(q,l,mid),merge_sort(q,mid+1,p);

    int k = 0, l = i,r = mid + 1;
	while(i>=p)
	if(q[l]<q[p]) tmp[k++] = q[l++];
	else tmp[k++] = q[p--];
	
	while(l<=mid) tmp(k++) = q[l++];
	while(r>=p) tmp(k++) = q[p--];
	
	for(int r = 0,l = i;r <= p;i++,k++) q[i]=tmp[r];
}

二、二分算法

1、整数二分算法

• 二分法，即二分搜索法，是通过不断缩小解可能存在的范围，从而求得问题最优解的方法。下面两种任用其一就行，分别求左右临界点，一般情况下左右临界点相等，除某些特殊题型需要查找出左边界和右边界。如：

起起始位置即左边界，终止位置即右边界。

• 图解：好吧，这个比较简单，博主就没找图啦，直接说原理！
• 其原理就是：先判断mid的值满足某种条件，于是可以将边界点左右俩边分为满足此条件和不满足此条件，如果mid的值满足此条件说明查找值在不满足此条件的值的那边。为了更好的理解，举个例子：猜数字玩过吧，比如这0-1000这个数字，第一次猜测为500，对方如果反馈数字大了，则说明要猜测的数字在0-499之间，如果反馈猜小了，那么说明要猜测的数字就在501-999之间。

还没看懂的小可爱可以结合代码理解哦

代码如下（示例）：

bool cheak(int x) {/****/}//检验x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int binarysearch_1(int l,int r)//向左查找，寻找右临界点
{
	while(l<r)
	{
		int mid = (l + r) >> 1;
		if(cheak(mid)) r = mid;//如果x在mid左边，则另右端点等于mid
		else l = mid + 1;		
	}	
	return l;
}

// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int binarysearch_2(int l,int r)//向右查找，寻找左临界点
{
	while(l<r)
	{
		int mid = (l+r)>>1;
		if(cheak(mid)) l=mid;
		else r = mid-1;
	}
	return l;	
}

每次取中点，也就相当于分的过程，所以时间复杂度最坏的情况下用O (log n)来完成。

2、浮点数二分算法

• 和整数一样本质上也是寻找一个边界，和整数二分不同的是，浮点数不存在由于（整数）取整导致的边界问题，每次二分区间严格减半，因此比整数二分简单的多，每次更新边界时直接让r = mid或l = mid即可。当整个区间的长度足够小的时候（这里取的是10^-6）就可以认定找到了答案。

代码如下（示例）：

bool cheak(double x) {/****/}//检验x是否满足某种性质

double Fbinarysearch(double l,double r)
{
	const double eps = 1e-6;// eps 表示精度，取决于题目对精度的要求
	while(r - l > eps)
	{
		double mid = (l + r) >> 1;
		if(cheak(mid)) r = mid;
		else l = mid;
	}
	return l;
}

彩蛋，彩蛋！！

终于码完了！！！【哭!】

• 都康到这里了，彩蛋就是、就是：今年你肯定是yyds！！！（不是永远单身）

大佬：就这啊？
我：就这了【哭!】

后面还会持续更新，欢迎下方评论区留言，下期见！！！
下期内容：
一、高精度
二、前缀和与差分

作者：琉璃Diaspora