1.算法原理
2.改进点
改进发现者更新位置
为了使 SSA 算法能够避开向原点收敛的弊端, 将算法向最优位置跳跃的操作转换为向最优位置的移动:
X
i
,
j
t
+
1
=
{
X
i
,
j
t
⋅
(
Q
+
1
)
,
R
2
<
S
T
X
i
,
j
t
+
Q
,
R
2
⩾
S
T
(1)
\left.X_{i,j}^{t+1}=\left\{\begin{array}{ll}X_{i,j}^{t}\cdot(Q+1),&R_2<S T\\\\X_{i,j}^{t}+Q,&R_2\geqslant S T\end{array}\right.\right.\tag{1}
Xi,jt+1=⎩
⎨
⎧Xi,jt⋅(Q+1),Xi,jt+Q,R2<STR2⩾ST(1)
改进预警者更新位置
为了让预警者发现危险后能够逃离到最优的安全位置, 提高算法的全局搜索能力:
X
i
,
j
t
+
1
=
{
X
i
,
j
t
⋅
β
⋅
(
X
i
,
j
t
−
X
b
e
s
t
t
)
,
f
i
=
f
g
X
i
,
j
t
+
β
⋅
(
X
w
o
r
s
t
t
−
X
b
e
s
t
t
)
,
f
i
≠
f
g
(2)
\left.X_{i,j}^{t+1}=\left\{\begin{array}{ll}X_{i,j}^{t}\cdot\beta\cdot(X_{i,j}^{t}-X_{\mathrm{best}}^{t}),&f_{i}=f_{g}\\X_{i,j}^{t}+\beta\cdot(X_{\mathrm{worst}}^{t}-X_{\mathrm{best}}^{t}),&f_{i}\neq f_{g}\end{array}\right.\right.\tag{2}
Xi,jt+1={Xi,jt⋅β⋅(Xi,jt−Xbestt),Xi,jt+β⋅(Xworstt−Xbestt),fi=fgfi=fg(2)
高斯变异策略
引入高斯变异算子对每次迭代得到的全局最优解进行扰动, 避免算法陷入局部最优, 出现早熟现象的缺点, 同时也能够维持种群个体的多样性:
X
g
a
u
s
s
t
+
1
=
X
g
b
e
s
t
t
⋅
(
1
+
G
a
u
s
s
i
a
n
(
α
)
)
(3)
X_{\mathrm{gauss}}^{t+1}=X_{\mathrm{gbest}}^{t}\cdot(1+Gaussian(\alpha))\tag{3}
Xgausst+1=Xgbestt⋅(1+Gaussian(α))(3)
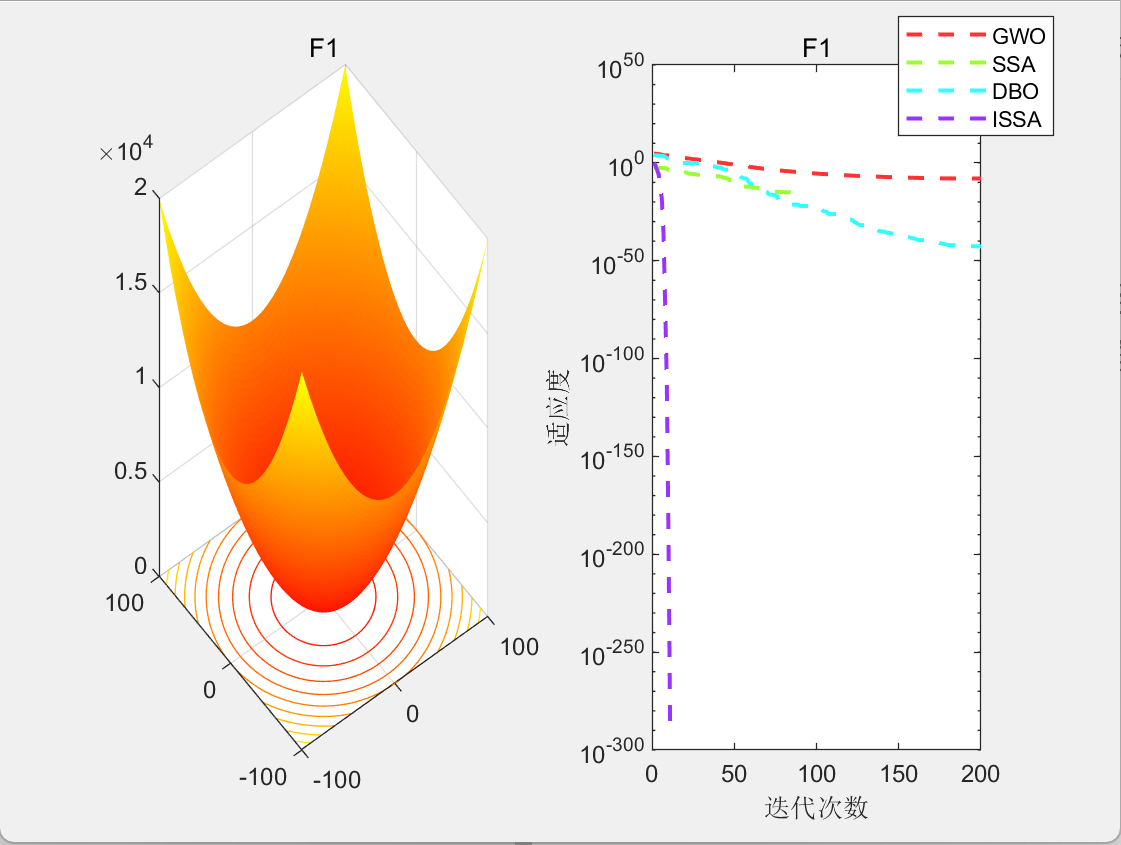
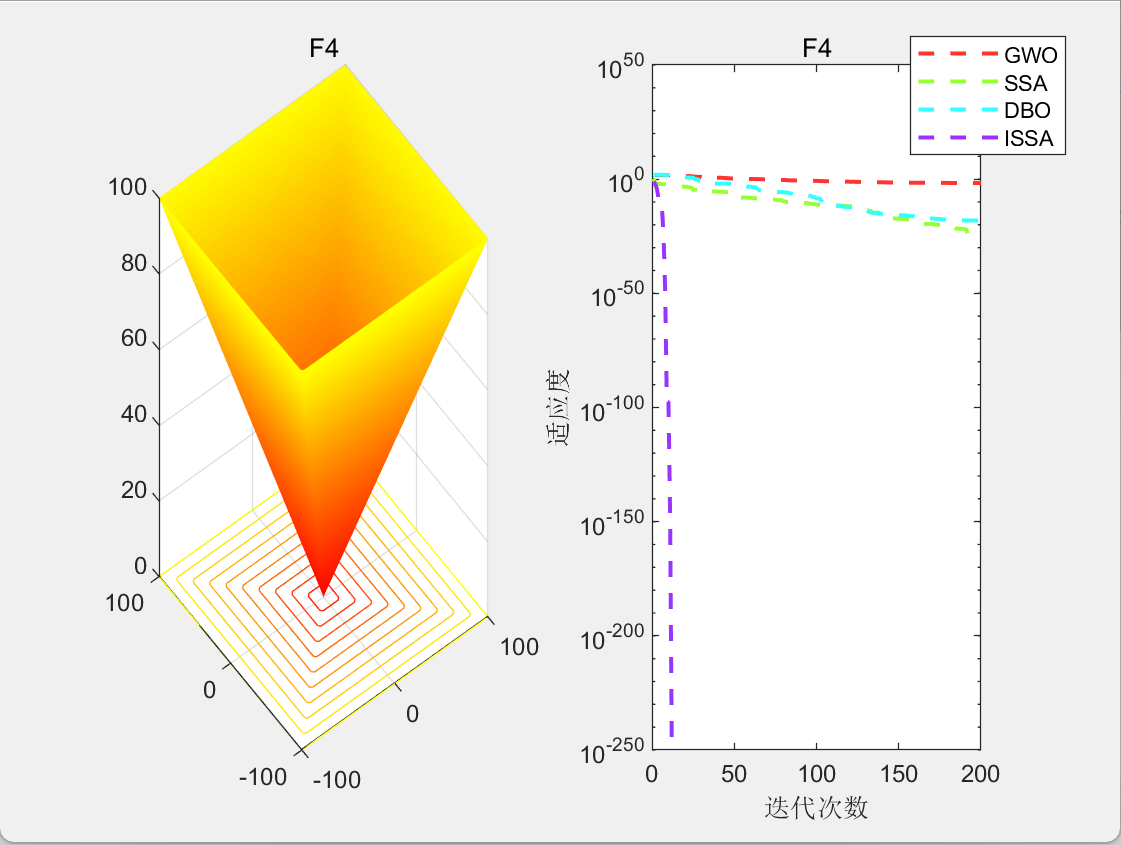
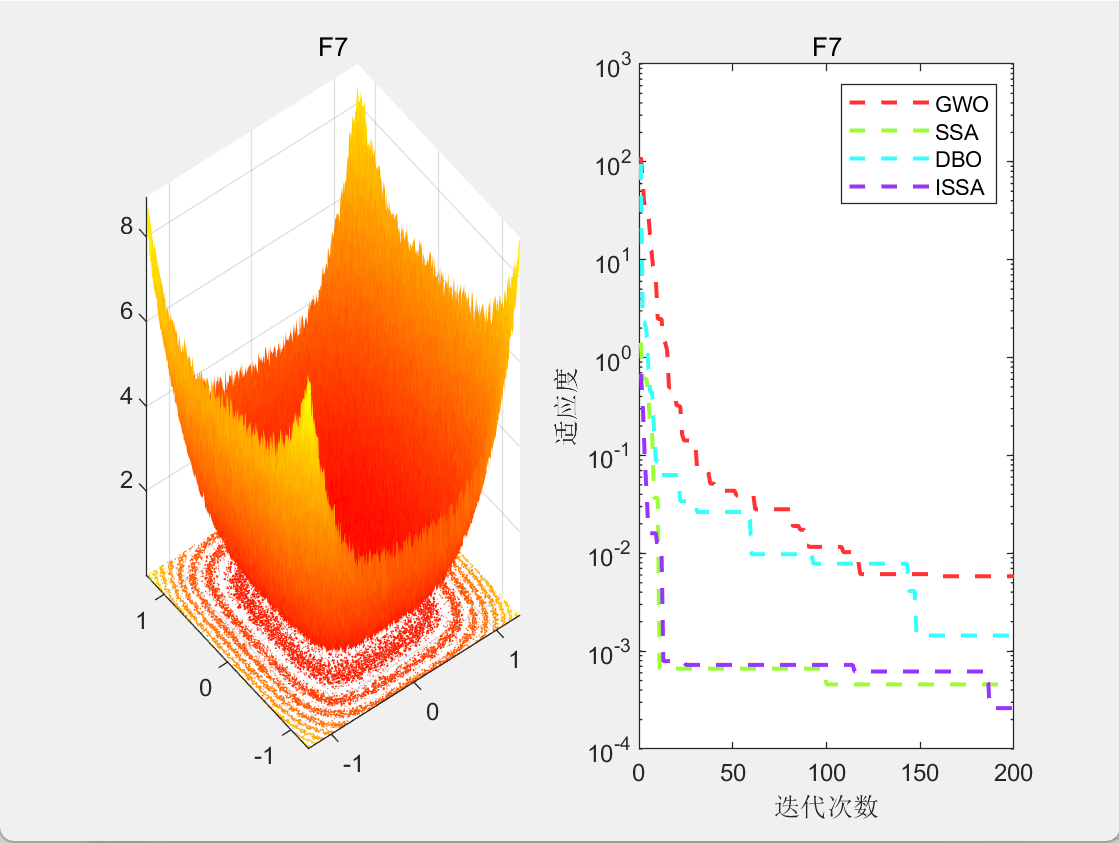
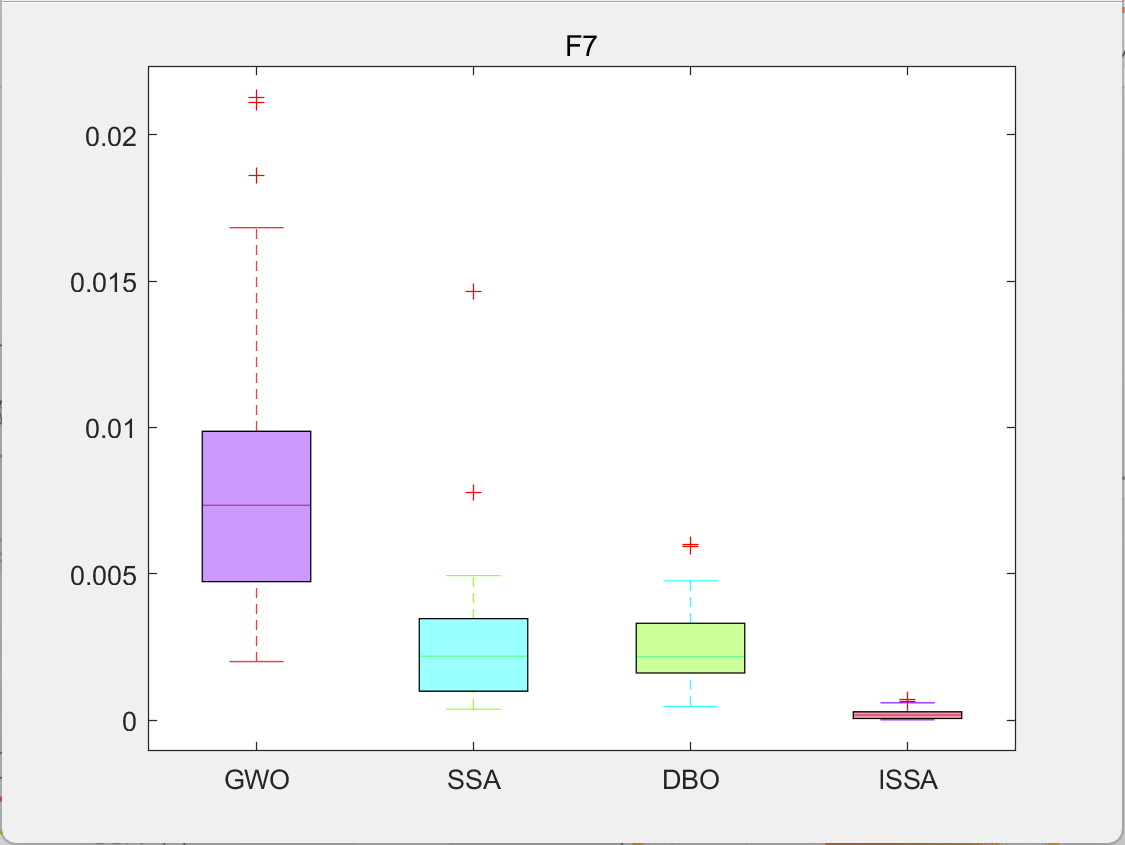
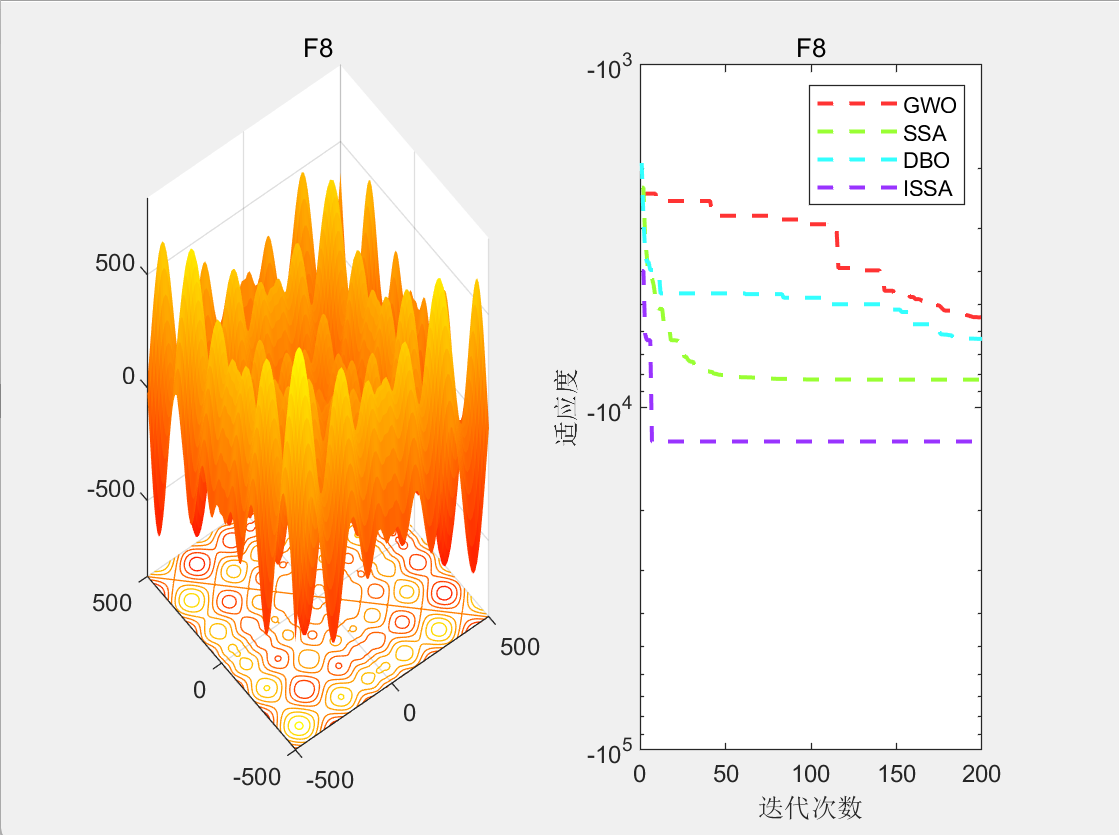
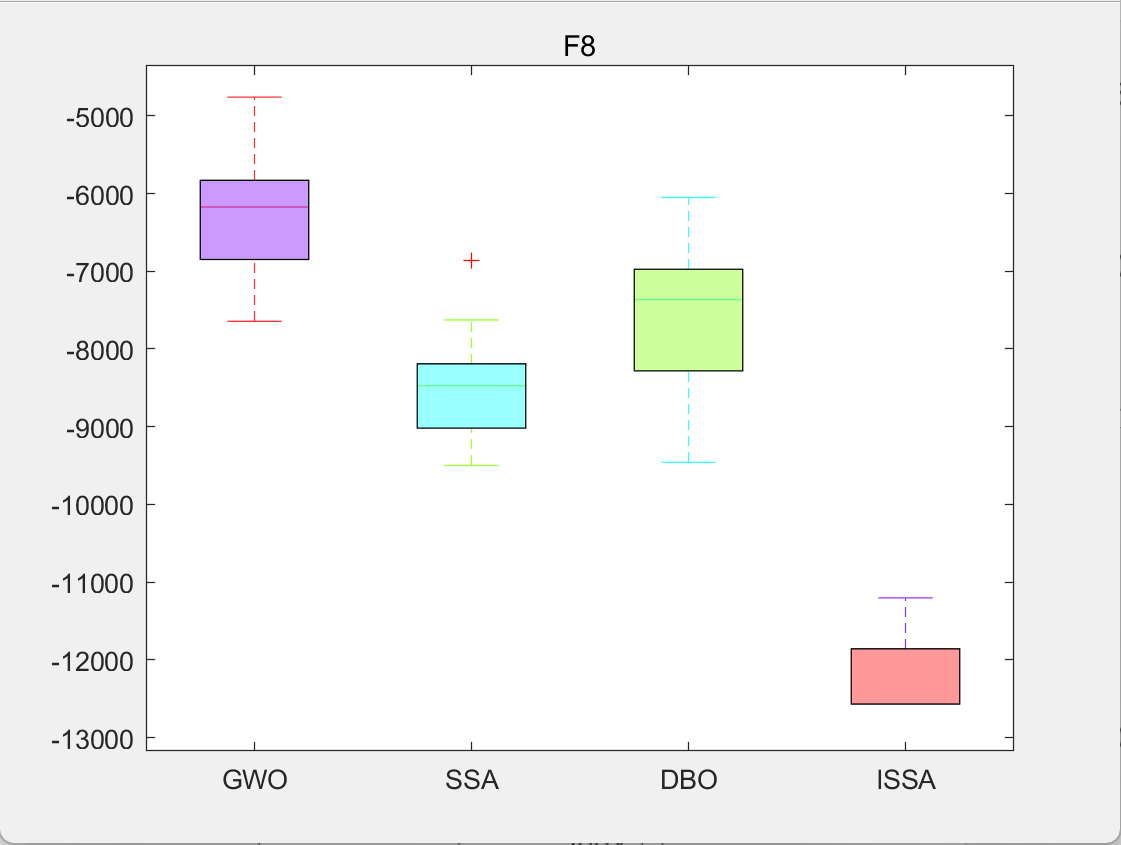
3.结果展示
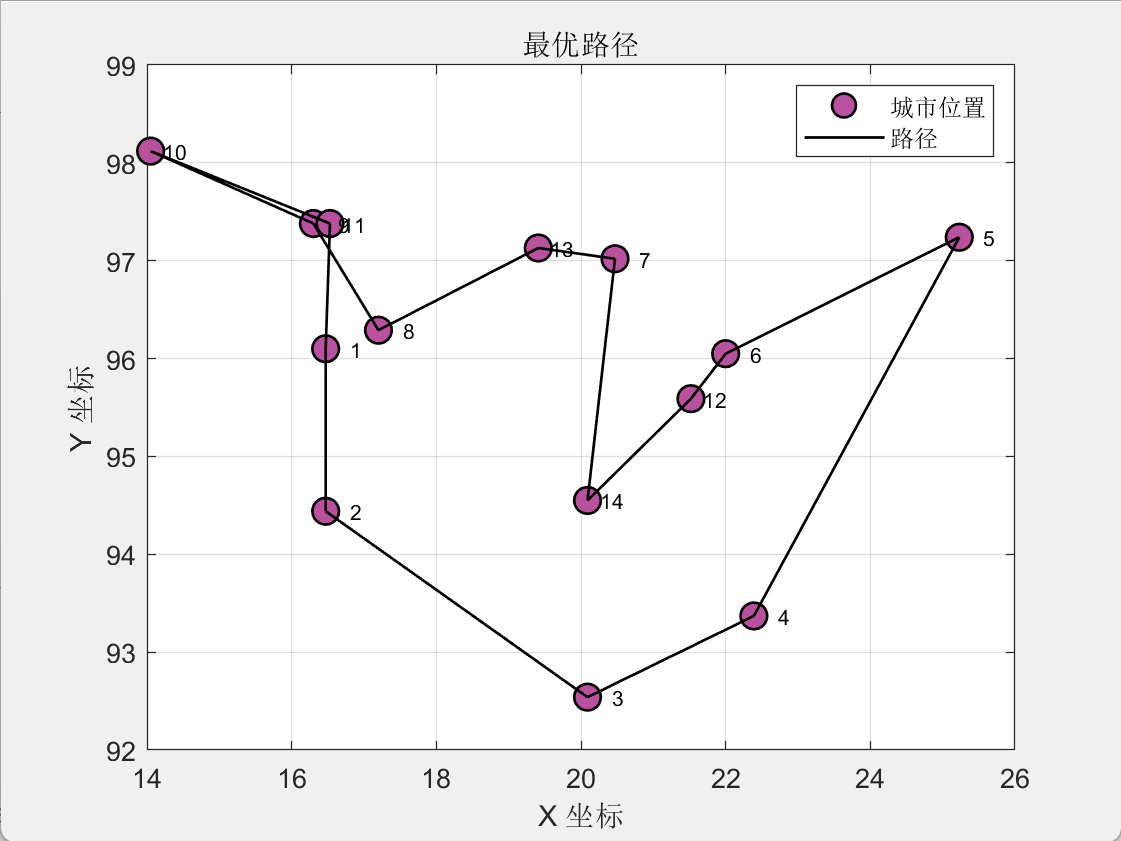
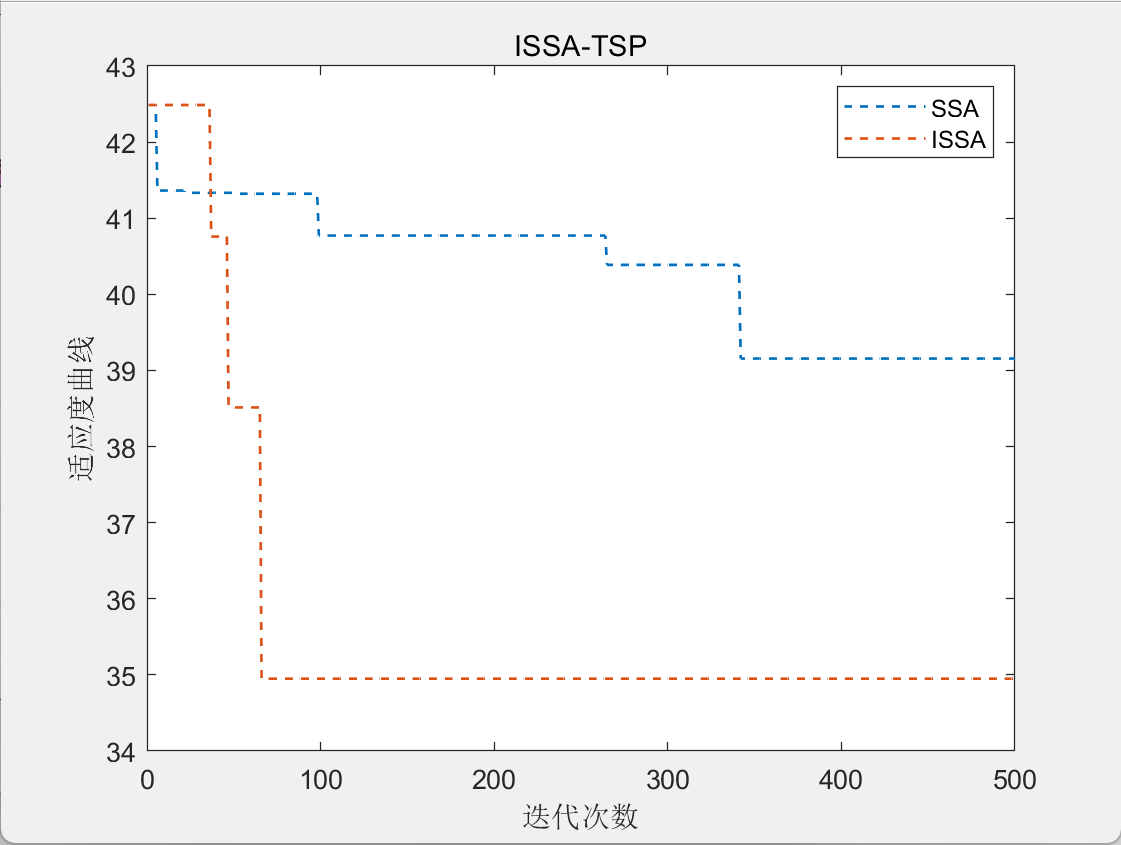
TSP应用
4.参考文献
[1] 张月栋,莫愿斌.改进的麻雀搜索算法及其求解旅行商问题.计算机系统应用,2022,31(2):200-206