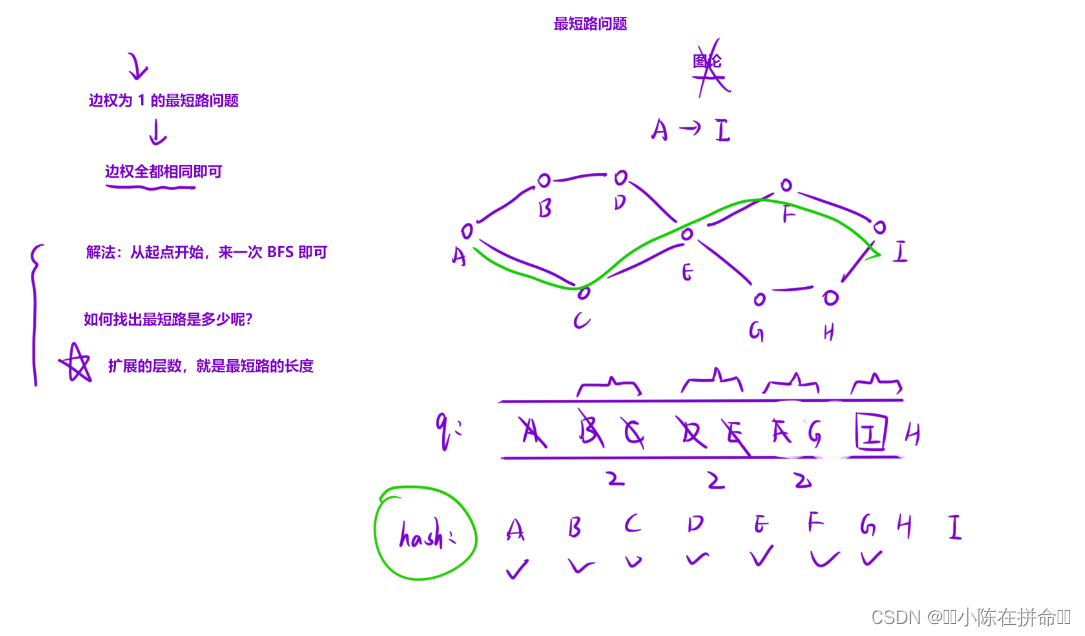
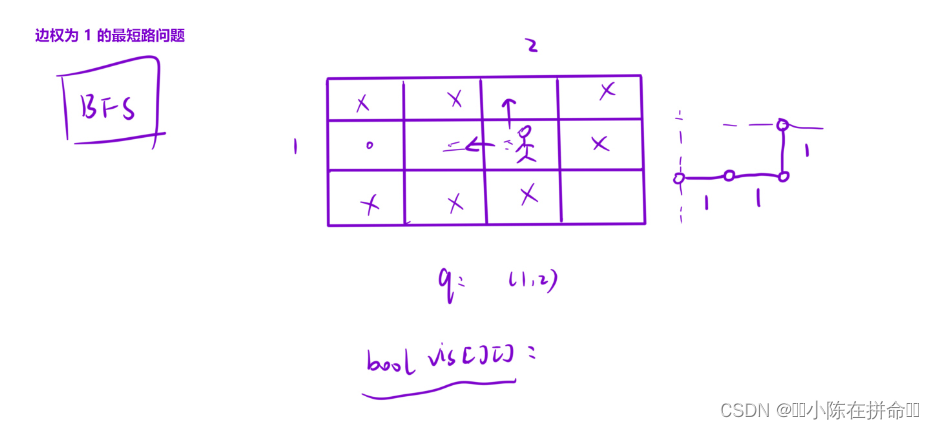
一、边权相同最短路问题简介
二、迷宫中离入口最近的出口
class Solution {
public:
const int dx[4]={1,-1,0,0};
const int dy[4]={0,0,1,-1};
int nearestExit(vector<vector<char>>& maze, vector<int>& e) {
int m=maze.size(),n=maze[0].size();
queue<pair<int,int>> q;//队列
bool check[m][n]; //非全局的bool是乱值 全局的会初始化为0
//力扣支持这样的写法
memset(check,0,sizeof(check)); //初始化成0
q.emplace(e[0],e[1]);
check[e[0]][e[1]]=true;
int step=0;//统计步数
while(!q.empty())
{
++step;
//要控制同一层出
int sz=q.size();
for(int i=0;i<sz;++i)
{
auto[a,b]=q.front();
q.pop();
for(int k=0;k<4;++k)
{
int x=dx[k]+a,y=dy[k]+b;
if(x>=0&&x<m&&y>=0&&y<n&&maze[x][y]=='.'&&check[x][y]==false)
{
//如果找到最后一个了,就可以直接返回了
if(x==0||x==m-1||y==0||y==n-1) return step;
//如果没找到,继续进
q.emplace(x,y);
check[x][y]=true;
}
}
}
}
return -1;
}
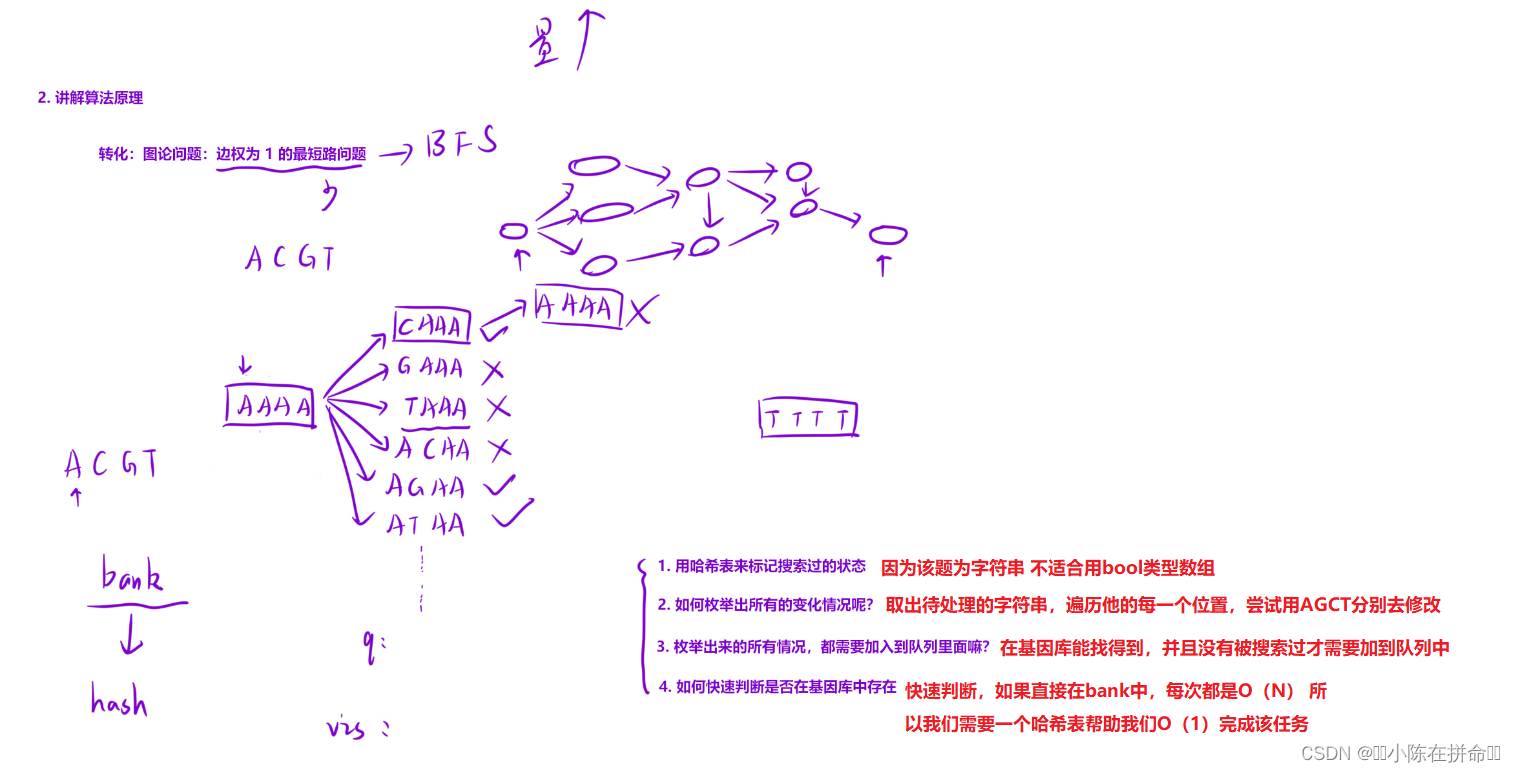
};三、最小基因变化(经典图论bfs)
class Solution {
public:
//转化成图论中的bfs问题
int minMutation(string startGene, string endGene, vector<string>& bank) {
if(startGene==endGene) return 0;
string s("AGCT");//四种变化情况
unordered_set<string> hash1(bank.begin(),bank.end());//负责帮助我们快速查找字符串是否在基因库中
if(hash1.count(endGene)==0) return -1;
queue<string> q;//存储在基因库中出现过的变化后字符串
q.emplace(startGene);
unordered_set<string> hash2;//负责标记哪些字符串被搜索过
hash2.insert(startGene);
int step=0;//用来统计步数
while(!q.empty())
{
++step;
int sz=q.size();//控制一行一行出
for(int i=0;i<sz;++i)
{
string temp=q.front();//待处理的字符串
q.pop();
for(int j=0;j<8;++j) //遍历字符串的每个位置
{
for(int k=0;k<4;++k)
{
string cur=temp;
cur[j]=s[k];//修改
if(hash1.count(cur)&&hash2.count(cur)==0)//如果基因库找到了 就丢进去
{
if(cur==endGene) return step;
hash2.insert(cur);
q.emplace(cur);
}
}
}
}
}
return -1;
}
};四、单词接龙
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
int n=beginWord.size();
//需要一个哈希表存储字典中的字符串,方便快速搜索是否存在
unordered_set<string> hash(wordList.begin(),wordList.end());
//需要一个标记哈希表帮助我们判断被搜索过的字符串
if(!hash.count(endWord)) return 0;
unordered_set<string> vis;
queue<string> q;
vis.insert(beginWord);
q.emplace(beginWord);
int ret=1;
while(!q.empty())
{
++ret;
//要控制一行一行出
int sz=q.size();
for(int i=0;i<sz;++i)
{
string t=q.front();
q.pop();
//开始想办法修改
for(int j=0;j<n;++j) //遍历字符串的每个位置
for(char k='a';k<='z';++k)
{
string temp=t;
temp[j]=k;//修改
//如果修改后在字典中找到,就可以加入队列中 如果是最终结果就返回
if(hash.count(temp)&&!vis.count(temp))
{
if(temp==endWord) return ret;
vis.insert(temp);
q.emplace(temp);
}
}
}
}
return 0;
}
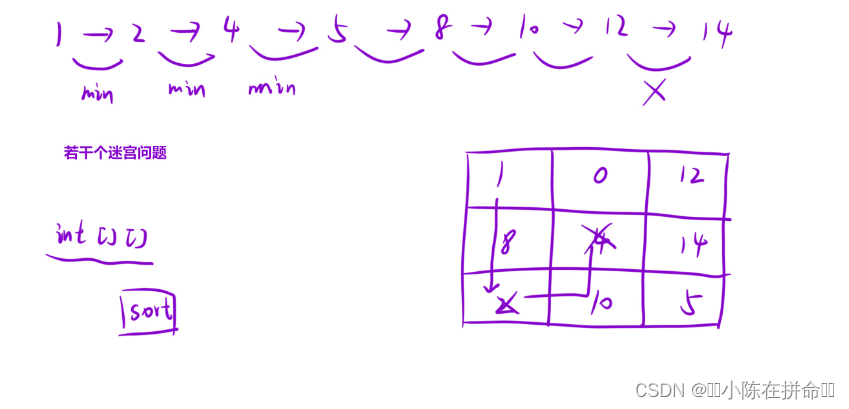
};五、为高尔夫比赛砍树(经典bfs)
转化成多个最短路问题,但是我们需要知道从哪树开始砍,第一个方法就是用map进行存储,可以顺便帮助我们排序,第二个方法就是用vector进行存储,然后sort+lambda表达式解决问题
策略1:用map
class Solution {
public:
typedef pair<int,int> PII;
int m,n;
const int dx[4]={1,-1,0,0};
const int dy[4]={0,0,1,-1};
int cutOffTree(vector<vector<int>>& f) {
//转化成若干个迷宫问题
//得存下标和值 并且要方便排序
m=f.size(),n=f[0].size();
map<int,PII> hash;//前面存值 后面存下标
for(int i=0;i<m;++i)
for(int j=0;j<n;++j)
if(f[i][j]>1) hash[f[i][j]]=make_pair(i,j); //map会帮助我们排好序
//然后按顺序砍树
int bx=0,by=0; //初始位置
int ret=0;
for(auto&it:hash)
{
auto&[a,b]=it.second;
int step=bfs(f,bx,by,a,b);
if(step==-1) return -1;
ret+=step;
//往下迭代
bx=a,by=b;
}
return ret;
}
bool vis[50][50];
int bfs(vector<vector<int>>& f,int bx,int by,int a,int b)
{
//转化成迷宫问题 从起点到终点的最短路问题
if(bx==a&&by==b) return 0; //有可能直接从起始位置开始砍
queue<PII> q;
//必须要清空之前的数据
memset(vis,0,sizeof(vis));
q.emplace(bx,by);
vis[bx][by]=true;
int step=0;
while(!q.empty())
{
//要控制一层一层走
++step;
int sz=q.size();
for(int i=0;i<sz;++i)
{
auto[ex,ey] =q.front();
q.pop();
for(int k=0;k<4;++k)
{
int x=dx[k]+ex,y=dy[k]+ey;
if(x>=0&&x<m&&y>=0&&y<n&&f[x][y]!=0&&vis[x][y]==false)
{
if(x==a&&y==b) return step;
//丢进去
q.emplace(x,y);
vis[x][y]=true;
}
}
}
}
return -1;
}
};策略2:vector+sort+lambda
class Solution {
public:
typedef pair<int,int> PII;
int m,n;
const int dx[4]={1,-1,0,0};
const int dy[4]={0,0,1,-1};
int cutOffTree(vector<vector<int>>& f) {
//转化成若干个迷宫问题 关键就在于我们怎么确定砍树的顺序
//得存下标和值 并且要方便排序
m=f.size(),n=f[0].size();
//用一个vector存储下标,然后排序的时候用lambda表达式
vector<PII> trees;
for(int i=0;i<m;++i)
for(int j=0;j<n;++j)
if(f[i][j]>1) trees.emplace_back(i,j);
//sort+lambda 进行排序
sort(trees.begin(),trees.end(),[&f](const PII&kv1,const PII&kv2) //lambda捕获f
{
return f[kv1.first][kv1.second]<f[kv2.first][kv2.second];
});
//然后按顺序砍树
int bx=0,by=0; //初始位置
int ret=0;
for(auto&[a,b]:trees)
{
int step=bfs(f,bx,by,a,b);
if(step==-1) return -1;//说明无路可走了
ret+=step;
//往下迭代
bx=a,by=b;
}
return ret;
}
bool vis[50][50];
int bfs(vector<vector<int>>& f,int bx,int by,int a,int b)
{
//转化成迷宫问题 从起点到终点的最短路问题
if(bx==a&&by==b) return 0; //有可能直接从起始位置开始砍
queue<PII> q;
//必须要清空之前的数据
memset(vis,0,sizeof(vis));
//如果不定义成全局的标记数据的话, 也可以定义成局部的标记数组,但同样需要进行初始化
q.emplace(bx,by);
vis[bx][by]=true;
int step=0;
while(!q.empty())
{
//要控制一层一层走
++step;
int sz=q.size();
for(int i=0;i<sz;++i)
{
auto[ex,ey] =q.front();
q.pop();
for(int k=0;k<4;++k)
{
int x=dx[k]+ex,y=dy[k]+ey;
if(x>=0&&x<m&&y>=0&&y<n&&f[x][y]!=0&&vis[x][y]==false)
{
if(x==a&&y==b) return step;
//丢进去
q.emplace(x,y);
vis[x][y]=true;
}
}
}
}
return -1;
}
};