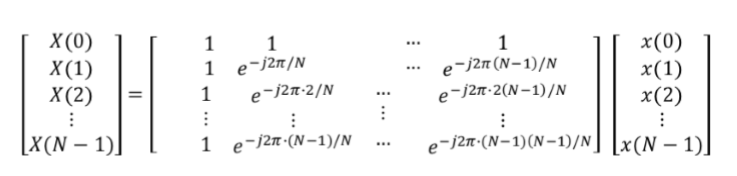【语音识别入门】特征提取（Python完整代码）

1、数字信号处理基础

1.1数字信号处理基础

在科学和工程中遇到的大多数信号都是连续模拟信号，例如电压随着时间变化，一天中温度的变化等等，而计算机智能处理离散的信号，因此必须对这些连续的模拟信号进行转化。通过采样–量化来转换成数字信号。
以正弦波为例：
$x (t) = s in (2Π f * t)$

( $f$ 表示信号本身的频率，单位 $Hz$ )
首先对正弦波进行采样，每 $t$ 秒进行一次采用，并使用一定范围的离散数值来表示采样值，得到离散信号 $x (n)$ :
$x (n) = s in (2Π f * n t)$

1.2频率混叠

由于采样信号频谱发生变化，而出现高、低频成分发生混淆的一种现象。抽样时频率不够高，抽样出来的点既代表了信号中的低频信号的样本值，也同时代表高频信号样本值，在信号重建的时候，高频信号被低频信号代替，两种波形完全重叠在一起，形成严重失真。

1.3 奈奎斯特采样定理

采样频率要大于信号中最大频率的两倍
$f s /2 \geq f ma x$
即在原始信号的一个周期内至少要采样两个点才能有效杜绝频率混叠问题

1.4 离散傅里叶变换（DFT）

DFT将时域离散且周期的信号的时域变换到频域，分析信号中的频率成分，若是非周期的离散信号需要进行周期延拓再进行DFT。

在这里插入图片描述
DFT在时域和频域上都具有离散和周期的特点，可用于计算机处理

在这里插入图片描述

1.5 DFT的性质

对称性 $X (m) = X * (N - m)$
线性
时移性

2、特征提取流程

Fbank和MFCC提取流程
在这里插入图片描述

2.1预加重(preemphasis)

提高信号高频部分能量
预加重滤波器是一个一阶高通滤波器，给定时域输入信号 $x [n]$ ，预加重后的信号为 $y [n] = x [n] - a * x [n - 1]$ ，其中 $0.9 <= a <= 1.0$

代码

np.append(signal[0], signal[1:] - coeff * signal[:-1])

2.2加窗分帧（enframe）

语音信号为非平稳信号，其统计属性是随着时间变化的；语音信号又具有短时平稳的属性，在进行语音识别的时候，对于一句话，识别的过程也是以较小的发音单元（音素、字音素或者字、字节）为单位进行识别，因此用滑动窗来提取短时片段
、帧长、帧移、窗函数，对于采样率为16kHz的信号，帧长、帧移一般为25ms、10ms即400和160个采样点。分帧的过程，在时域上即是用一个窗函数和原始信号进行相乘 $y [n] = w [n] x [n]$ , $w [n]$ 为窗函数，常用矩形窗和汉明窗。注在加窗的过程中一般不直接使用矩形窗，实际上是在时域上将信号截断，窗函数与信号在时域相乘，就等于对应的频域表示进行卷积，矩形窗主瓣窄但是旁瓣较大，将其与原信号的频域表示进行卷积就会导致频率泄露。

代码

def enframe(signal, frame_len=frame_len, frame_shift=frame_shift, win=np.hamming(frame_len)):
    """Enframe with Hamming widow function.

        :param signal: The signal be enframed
        :param win: window function, default Hamming
        :returns: the enframed signal, num_frames by frame_len array
    """
    num_samples = signal.size
    // num_frames表示总共有多少个帧
    // 帧长frame_len表示一帧 包含多少个点
    // 帧移frame_shift表示一个帧移 包含多少个点
    num_frames = np.floor((num_samples - frame_len) / frame_shift) + 1
    frames = np.zeros((int(num_frames), frame_len))
    for i in range(int(num_frames)):
        frames[i, :] = signal[i * frame_shift:i * frame_shift + frame_len]
        frames[i, :] = frames[i, :] * win
    return frames

2.3傅里叶变换

经过上一步分帧之后的语音帧，已经从时域变换到了频域，取DFT系数的模，得到谱特征。（语谱图的生成）

#DFT具有对称性，在N点DFT之后，只需要保证前N/2+1个点即可
def get_spectrum(frames, fft_len=fft_len):
    """Get spectrum using fft
        :param frames: the enframed signal, num_frames by frame_len array
        :param fft_len: FFT length, default 512
        :returns: spectrum, a num_frames by fft_len/2+1 array (real)
    """
    cFFT = np.fft.fft(frames, n=fft_len)
    valid_len = int(fft_len / 2) + 1
    spectrum = np.abs(cFFT[:, 0:valid_len])
    return spectrum

2.4梅尔滤波器组和对数操作

DFT得到了每个频带上信号的能量，但是人耳对频率的感知不是等间隔的，近似于对数函数。将线性频率转换为梅尔频率，梅尔频率和线性频率的转换关系是： $m e l = 2595 l o g 10 (1 + f /700)$

梅尔三角滤波器组：根据起始频率、中间频率和截止频率，确定各滤波系数

梅尔滤波器组设计：

（1）确定滤波器组个数P
（2）根据采样率 $f s$ ，DFT点数N，滤波器个数P，在梅尔域上等间隔的产生每个滤波器的起始频率，中间频率和截止频率，注意，上一个滤波器的中间频率为下一个滤波器的起始频率（存在overlap）
（3）将梅尔域上每个三角滤波器的起始、中间和截止频率转换线性频率域，并对DFT之后的谱特征进行滤波，得到P个滤波器组能量，进行log操作，得到FBank特征
MFCC特征在FBank特征的基础上继续进行IDFT变换等操作。

代码

def mel_filter(frame_pow, fs, n_filter, nfft):
    """
    mel 滤波器系数计算
    :param frame_pow: 分帧信号功率谱
    :param fs: 采样率 hz
    :param n_filter: 滤波器个数
    :param nfft: fft点数
    :return: 分帧信号功率谱mel滤波后的值的对数值
    mel = 2595 * log10(1 + f/700)   # 频率到mel值映射
    f = 700 * (10^(m/2595) - 1      # mel值到频率映射
    上述过程本质上是对频率f对数化
    """
    mel_min = 0     # 最低mel值
    mel_max = 2595 * np.log10(1 + fs / 2.0 / 700)   # 最高mel值，最大信号频率为 fs/2
    mel_points = np.linspace(mel_min, mel_max, n_filter + 2)    # n_filter个mel值均匀分布与最低与最高mel值之间
    hz_points = 700 * (10 ** (mel_points / 2595.0) - 1)     # mel值对应回频率点，频率间隔指数化
    filter_edge = np.floor(hz_points * (nfft + 1) / fs)     # 对应到fft的点数比例上
    
    # 求mel滤波器系数
    fbank = np.zeros((n_filter, int(nfft / 2 + 1)))
    for m in range(1, 1 + n_filter):
        f_left = int(filter_edge[m - 1])     # 左边界点
        f_center = int(filter_edge[m])       # 中心点
        f_right = int(filter_edge[m + 1])    # 右边界点
        
        for k in range(f_left, f_center):
            fbank[m - 1, k] = (k - f_left) / (f_center - f_left)
        for k in range(f_center, f_right):
            fbank[m - 1, k] = (f_right - k) / (f_right - f_center)
    
    # mel 滤波
    # [num_frame, nfft/2 + 1] * [nfft/2 + 1, n_filter] = [num_frame, n_filter]
    filter_banks = np.dot(frame_pow, fbank.T)
    filter_banks = np.where(filter_banks == 0, np.finfo(float).eps, filter_banks)
    # 取对数
    filter_banks = 20 * np.log10(filter_banks)  # dB
    return filter_banks

2.5动态特征计算

一阶差分（△） $△ t = (c (t + 1) - c (t - 1)) /2$ （类比速度）
二阶差分（△△） $△△ t = (△ (t + 1) - △ (t - 1)) /2$

2.6能量计算

$e = \sum x^{2} [n]$
MFCC特征总结：一般常用的MFCC特征是39维，包括12维原始MFCC+12维一阶差分+12维二阶差分—+1维原始能量+一维一阶能量+一维二阶能量
MFCC特征一般用于对角GMM训练，各维度之间相关性小；
FBank特征一般用于DNN训练。

代码

#前面提取到的FBank特征，往往是高度相关的。因此可以继续用DCT(离散余弦变换)变换，将这些相关的滤波器组系数进行压缩。对于ASR来说，通常取2~13维，扔掉的信息里面包含滤波器组系数快速变化部分
num_ceps = 12
mfcc = dct(filter_banks, type=2, axis=1, norm='ortho')[:, 1:(num_ceps+1)]
plot_spectrogram(mfcc.T, 'MFCC Coefficients')

3、Feature-extraction实践

给定一段音频，请提取12维MFCC特征和23维FBank，阅读代码预加重、分帧、加窗部分，完善作业代码中FBank特征提取和MFCC特征提取部分，并给出最终的FBank特征和MFCC特征，存储在纯文本中，用默认的配置参数，无需进行修改。

3.1代码文件说明

代码依赖
python3
librosa
如果需要观察特征频谱，请确保自己有matplotlib依赖并将代码中相关注解解掉
注：不要修改文件默认输出test.fbank test.mfcc的文件名

3.2文件路径说明

mfcc.py 作业代码
test.wav 测试音频
Readme.md 说明文件

3.3实验完整代码

import librosa
import numpy as np
from scipy.fftpack import dct
# If you want to see the spectrogram picture
import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as plt
def plot_spectrogram(spec, note,file_name):
    """Draw the spectrogram picture
        :param spec: a feature_dim by num_frames array(real)
        :param note: title of the picture
        :param file_name: name of the file
    """
    fig = plt.figure(figsize=(20, 5))
    heatmap = plt.pcolor(spec)
    fig.colorbar(mappable=heatmap)
    plt.xlabel('Time(s)')
    plt.ylabel(note)
    plt.tight_layout()
    plt.savefig(file_name)


#preemphasis config 
alpha = 0.97

# Enframe config
frame_len = 400      # 25ms, fs=16kHz
frame_shift = 160    # 10ms, fs=15kHz
fft_len = 512

# Mel filter config
num_filter = 23
num_mfcc = 12

# Read wav file
wav, fs = librosa.load('./test.wav', sr=None)

# Enframe with Hamming window function
def preemphasis(signal, coeff=alpha):
    """perform preemphasis on the input signal.

        :param signal: The signal to filter.
        :param coeff: The preemphasis coefficient. 0 is no filter, default is 0.97.
        :returns: the filtered signal.
    """
    return np.append(signal[0], signal[1:] - coeff * signal[:-1])

def enframe(signal, frame_len=frame_len, frame_shift=frame_shift, win=np.hamming(frame_len)):
    """Enframe with Hamming widow function.

        :param signal: The signal be enframed
        :param win: window function, default Hamming
        :returns: the enframed signal, num_frames by frame_len array
    """
    
    num_samples = signal.size
    num_frames = np.floor((num_samples - frame_len) / frame_shift)+1
    frames = np.zeros((int(num_frames),frame_len))
    for i in range(int(num_frames)):
        frames[i,:] = signal[i*frame_shift:i*frame_shift + frame_len] 
        frames[i,:] = frames[i,:] * win

    return frames

def get_spectrum(frames, fft_len=fft_len):
    """Get spectrum using fft
        :param frames: the enframed signal, num_frames by frame_len array
        :param fft_len: FFT length, default 512
        :returns: spectrum, a num_frames by fft_len/2+1 array (real)
    """
    cFFT = np.fft.fft(frames, n=fft_len)
    valid_len = int(fft_len / 2 ) + 1
    spectrum = np.abs(cFFT[:,0:valid_len])
    return spectrum

def fbank(spectrum, num_filter = num_filter):
    """Get mel filter bank feature from spectrum
        :param spectrum: a num_frames by fft_len/2+1 array(real)
        :param num_filter: mel filters number, default 23
        :returns: fbank feature, a num_frames by num_filter array 
        DON'T FORGET LOG OPRETION AFTER MEL FILTER!
    """
    low_mel_freq = 0
    high_mel_freq = 2595 * np.log10(1+(fs /2)/700) #转到梅尔尺度上
    mel_filters_points = np.linspace(low_mel_freq,high_mel_freq,num_filter+2)
    freq_filters_pints = (700 * (np.power(10.,(mel_filters_points/2595))-1))
    freq_bin = np.floor(freq_filters_pints / (fs /2)*(fft_len /2 + 1))
    feats=np.zeros((int(fft_len/2+1), num_filter))
    for  m in range(1,num_filter+1):
        bin_low = int(freq_bin[m-1])
        bin_medium = int(freq_bin[m])
        bin_high = int(freq_bin[m+1])
        for k in range(bin_low,bin_medium):
            feats[k,m-1]=(k-freq_bin[m-1])/(freq_bin[m]-freq_bin[m-1])
        for k in range(bin_medium,bin_high):
            feats[k,m-1]=(freq_bin[m+1]-k)/(freq_bin[m+1]-freq_bin[m])
    feats = np.dot(spectrum,feats)
    feats = 20 *np.log10(feats)
    return feats

def mfcc(fbank, num_mfcc = num_mfcc):
    """Get mfcc feature from fbank feature
        :param fbank: a num_frames by  num_filter array(real)
        :param num_mfcc: mfcc number, default 12
        :returns: mfcc feature, a num_frames by num_mfcc array 
    """

    #feats = np.zeros((fbank.shape[0],num_mfcc))
    mfcc = dct(fbank, type=2, axis=1, norm='ortho')[:, 1:(num_mfcc+1)]
    return mfcc

def write_file(feats, file_name):
    """Write the feature to file
        :param feats: a num_frames by feature_dim array(real)
        :param file_name: name of the file
    """
    f=open(file_name,'w')
    (row,col) = feats.shape
    for i in range(row):
        f.write('[')
        for j in range(col):
            f.write(str(feats[i,j])+' ')
        f.write(']\n')
    f.close()


def main():
    wav, fs = librosa.load('./test.wav', sr=None)
    signal = preemphasis(wav)
    frames = enframe(signal)
    spectrum = get_spectrum(frames)
    fbank_feats = fbank(spectrum)
    mfcc_feats = mfcc(fbank_feats)
    plot_spectrogram(fbank_feats, 'Filter Bank','fbank.png')
    write_file(fbank_feats,'./test.fbank')
    plot_spectrogram(mfcc_feats.T, 'MFCC','mfcc.png')
    write_file(mfcc_feats,'./test.mfcc')


if __name__ == '__main__':
    main()

3.4实验结果

FBank：
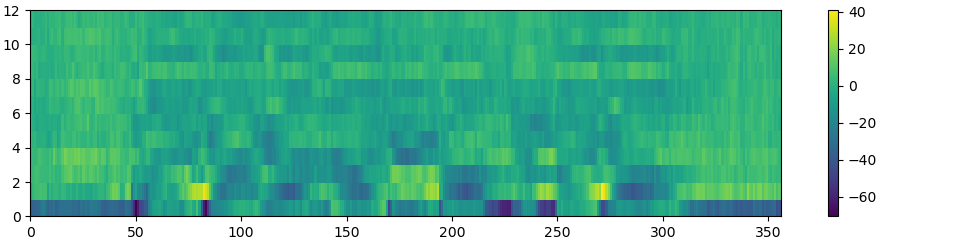
请添加图片描述

MFCC：
请添加图片描述