作业5 椭圆曲线加密算法

题目

在这里插入图片描述

答题

10.12

X的可能值（0到p-1）	0	1	2	3	4	5	6
$y^2=x^3+2x+1$	1	4	6	6	3	3	5
y对应的值	1,6	2,5

综上， $E_7(2,1)$ 的所有点为 $(0, 1), (0, 6), (1, 2), (1, 5)$

10.13

由于 $P + (- P) = O ， - P$ 表示x坐标相同，y坐标相反。

$\because P=(3,5),Q=(2,5),R=(5,0)$
$\therefore -P=(3,2),-Q=(2,2),-R=(5,0)$

10.14

根据公式
$R=P+Q:\begin{cases} x_R=\Delta ^2-x_P-x_Q \\ y_R=\Delta(x_P-x_R)-y_P\end{cases} \\ R=P+P=2P:\begin{cases} x_R= \Big( \frac {3x_P^2+a}{2y_P^{}} \Big) ^2-x_P-x_Q \\ y_R=\Big( \frac {3x_P^2+a}{2y_P^{}} \Big)(x_P-x_R)-y_P\end{cases}$

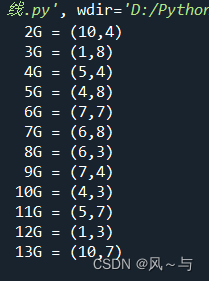
计算结果如下：

2G	3G	4G	5G	6G	7G	8G	9G	10G	11G	12G	13G
(10,4)	(1,8)	(5,4)	(4,8)	(7,7)	(6,8)	(6,3)	(7,4)	(4,3)	(5,7)	(1,3)	(10,7)

python代码

def egcd(a, b):
    if b == 0:
        return 1, 0
    else:
        x, y = egcd(b, a % b)
        return y, x-a//b*y


def ECC(a, x, y, p, time):
    s=[]
    i = 2
    # check 是否可以整除
    if ((3*x*x+a)%(2*y)) == 0:
        delta=int((3*x*x+a)/(2*y))%p
    else:
        _, inv = egcd(p, 2*y%p)
        delta = (3*x*x+a) * inv % p
    x1 = ((delta*delta)-2*x) % p
    y1 = (delta*(x-x1)-y) % p
    s.append((x1,y1))
    while i < time:
        i += 1
        # check 是否可以整除
        if ((y1-y)%(x1-x)) == 0:
            delta=int((y1-y)/(x1-x))%p
        else:
            _, inv = egcd(p, (x1-x)%p)
            delta = ((y1 - y) * inv) % p
        x1 = ((delta*delta)-x-x1) % p
        y1 = (delta*(x-x1)-y) % p
        s.append((x1,y1))
    return s


if __name__ == '__main__':
	a=1
	b=7
	xp=3
	yp=2
	p=11
	time=13
    s = ECC(a,xp,yp,p,time)
    i = 2
    for a in s:
        x=a[0]
        y=a[1]
        # check
        if(x**3+a*x+b)%p == (y*y)%p:
            print('{:3}G = ({},{})'.format(i, x, y))
        i+=1

运行结果