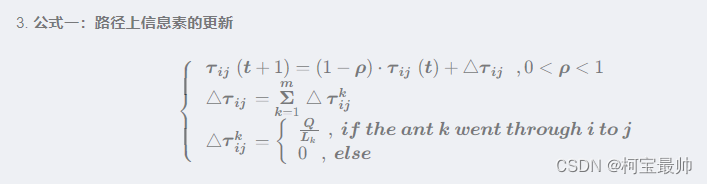一、优化问题

在满足一定条件下，在众多方案或参数中寻找最优方案或参数值，以使得某个或多个功能指标达到最优，或使系统的某些性能指标达到最大值或最小值。

但是当系统复杂或非线性时，要遍历所有参数组合寻找最优会变得很困难——“组合爆炸”，所以我们需要优化算法。

广义来讲，优化算法可分单一目标优化和多目标优化两大类。单一目标优化如梯度下降算法、线性回归算法等；多目标优化如蚁群算法、粒子群算法、遗传算法、模拟退火算法、布谷鸟算法等（群智能算法）。

二、蚁群优化算法

蚁群优化算法（Ant Colony Optimization, ACO）是一种模拟自然界中蚂蚁觅食行为的启发式搜索算法，该算法通过模拟蚂蚁在寻找食物过程中释放并感知信息素（一种化学物质）的行为，来寻找优化问题的解。

1、基本原理

• 信息素与路径选择：
  • 蚂蚁在觅食过程中会在所经过的路径上释放信息素，这些信息素的浓度与路径的质量（如长度）成反比——路径越长，信息素越淡。
  • 后续蚂蚁在选择路径时会受到信息素浓度的影响，倾向于选择信息素浓度较高的路径。
• 正反馈机制：
  • 随着时间的推移，较优路径上的信息素浓度会逐渐累积，吸引更多的蚂蚁选择该路径，形成正反馈。
  • 最终，整个蚂蚁群体会集中在最优路径上，找到问题的最优解。

2、基本流程

• 初始化：
  • 设置算法参数，如蚁群规模、信息素因子（α）、启发函数因子（β）、信息素挥发因子（ρ）、信息素常数（Q）以及最大迭代次数等。
  • 初始化信息素矩阵，将所有路径上的信息素浓度设置为相同的初始值。
• 构建解空间：
  • 随机将蚂蚁放置于不同的出发点，每只蚂蚁根据当前的信息素浓度和启发式信息（如路径长度的倒数）选择下一个访问的城市，直到所有蚂蚁都访问完所有城市。
  • 
  • 公式解释：原公式是只根据信息素无启发函数因子。修改后的公式不仅考虑了信息素的影响因素，更重要的是引入了启发函数的概念，推进了该算法的进步。为了加快算法的收敛速度以及蚂蚁的选择准确性，我们选择给蚂蚁开一副“天眼”，利用我们已知的数据去促使蚂蚁在前期更容易选择更近的道路(并不代表每次选择最短的路径就是全局最优解，这是贪心的思想)，不会导致纯随机的选择结果，蚂蚁拥有该作弊器后在全局来看可以更快的选择更优的路径规划，最终尽量帮助蚁群找到全局最优解。

    信息素因子及启发函数因子的大小对于算法的收敛性具有很大影响，过高的信息素因子数值将导致蚂蚁放弃“天眼”，在前期的选择偏于随机；过高的启发函数因子数值将导致蚂蚁容易基于贪心的思想进行搜索，而贪心在大多数优化问题中并不能找到全局最优解。

• 计算路径长度：
  • 计算每只蚂蚁经过的路径长度，并记录当前迭代次数下的最优解。
• 更新信息素：
  • 根据蚂蚁构建的路径长度和信息素更新规则，更新路径上的信息素浓度。通常，信息素会随时间蒸发（乘以一个小于1的常数），同时蚂蚁在其经过的路径上释放新的信息素。
  • 
  • 
  • 
• 迭代与终止：
  • 重复构建解空间和更新信息素的步骤，直到达到最大迭代次数或满足其他终止条件。
  • 输出最优解及其相关信息。

3、特点与应用

• 特点：
  • 分布式并行计算：算法采用分布式并行计算机制，具有较强的鲁棒性。
  • 信息正反馈：通过信息素的正反馈机制，引导蚂蚁群体向最优解聚集。
  • 启发式搜索：算法结合了启发式信息和随机搜索策略，能够在复杂问题中找到较好的解。
• 应用：
  • 蚁群优化算法已广泛应用于旅行商问题（TSP）、车辆路径规划、网络路由优化等多种复杂的优化问题中。
  • 其他算法的参数优化。

三、Matlab算例——TSP问题

旅行商问题（TSP）：寻求旅行完所有城市总路径最短。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路经的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。TSP问题是一个组合优化问题。该问题可以被证明具有NPC计算复杂性。

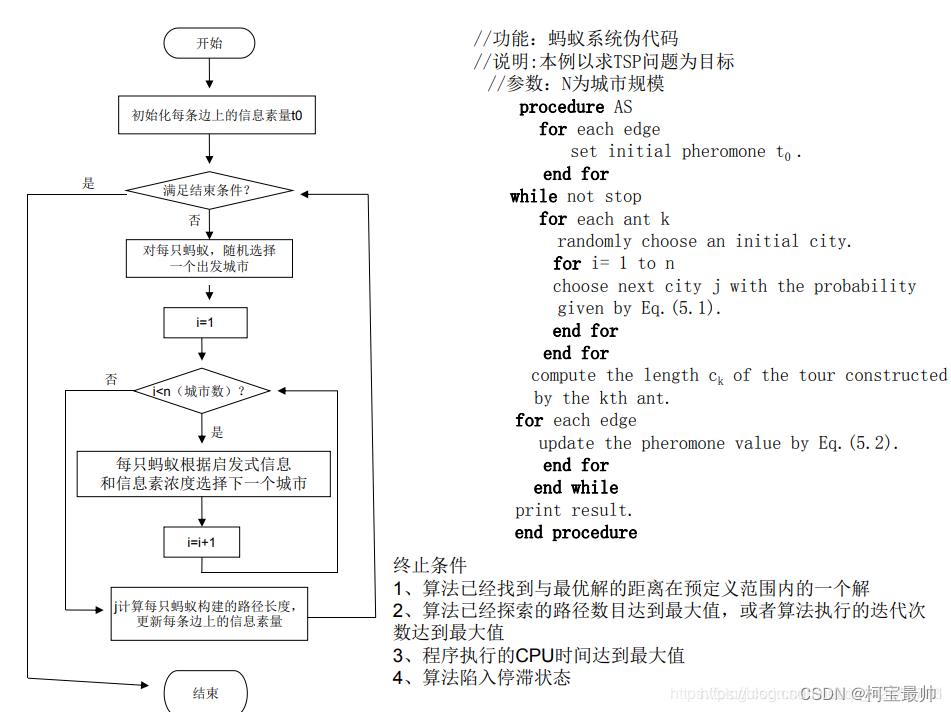
利用蚁群优化算法解决TSP问题，算法实现框架如下图：

①搜集城市节点坐标，并保存.mat数据

A=[1.304 2.312
3.639 1.315
4.177 2.244
3.712 1.399
3.488 1.535
3.326 1.556
3.238 1.229
4.897 5.468
1.987 2.687
6.359 6.987
10.479 11.674
9.657 6.845
7.687 6.945
12.467 10.367
15.164 14.267
17.654 14.983
1.302 7.635
2.346 9.647
3.647 10.943
12.001 2.036
11.746 1.357
9.467 2.467
14.605 6.876
16.798 5.304
4.304 8.674
5.476 14.379
16.004 7.649]
save('A.mat','A');

.mlx文件，该节输出：

②导入数据，数据预处理（将坐标转换为两城市距离）

%% 旅行商问题(TSP)优化
%% 清空环境变量
clear all
clc

%% 导入数据
load A.mat
% 将加载的变量A重命名为citys  
citys = A;  

%% 计算城市间相互距离
fprintf('Computing Distance Matrix... \n'); %向MATLAB的命令窗口输出一条消息，表明程序正在计算距离矩阵
n = size(citys,1); %获取行数，即城市数量
D = zeros(n,n);  %初始化一个零矩阵，存储第i个城市与第j个城市之间的距离
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
        else
            D(i,j) = 1e-4; % 通常我们将城市到自身的距离设为0，这里用一个非常小的数防止程序报错 
        end
    end    
end

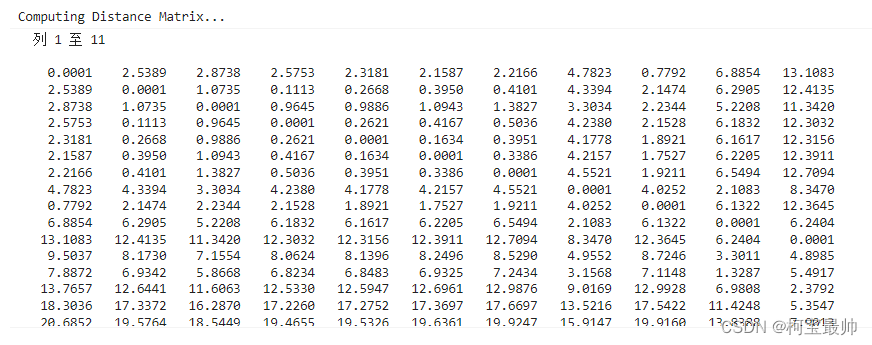
% （可选）显示距离矩阵D  
disp(D);

.mlx文件，该节输出：（只列出了前11行，共27行）

③初始化算法参数

%% 初始化参数
fprintf('Initializing Parameters... \n');%向MATLAB的命令窗口输出一条消息，表明程序正在初始化算法参数
m = 50;                              % 蚂蚁数量——5
alpha = 1;                           % 信息素重要程度因子——1
beta = 5;                            % 启发函数重要程度因子——5，说明启发函数的影响程度比信息素大
rho = 0.1;                           % 信息素挥发因子——0.1
Q = 1;                               % 常系数——1，蚂蚁完成一次旅行后，更新信息素时使用的常数
Eta = 1./D;                          % 启发函数是用于估计从当前节点到目标节点最佳路径成本的函数（表示对D中的每个元素取倒数，这里，1.是一个浮点数，确保除法操作是浮点除法（而不是整数除法）
Tau = ones(n,n);                     % 信息素矩阵——全1矩阵
Table = zeros(m,n);                  % 路径记录表——全0矩阵，用于记录每只蚂蚁的访问路径
iter = 1;                            % 迭代次数初值——1
iter_max = 100;                      % 最大迭代次数——100
Route_best = zeros(iter_max,n);      % 各代最佳路径       
Length_best = zeros(iter_max,1);     % 各代最佳路径的长度，每次迭代中找到的最佳路径及其长度  
Length_ave = zeros(iter_max,1);      % 各代路径的平均长度，每次迭代中所有蚂蚁路径的平均长度

.mlx文件，该节输出：

④算法核心/框架

详细注释了，便于一步步理解！

%% 迭代寻找最佳路径——包含了该算法的基本框架
figure;
while iter <= iter_max    %迭代次数——100
    fprintf('迭代第%d次\n',iter);
    % 随机产生各个蚂蚁的起点城市
      start = zeros(m,1);           %m：蚂蚁数量——50
      for i = 1:m                   %遍历50只蚂蚁，第i个蚂蚁
          temp = randperm(n);       %生成一个1到n的随机排列
          start(i) = temp(1);       %将随机排列的第一个元素作为第i只蚂蚁的起点
      end
      Table(:,1) = start;           %将所有蚂蚁的起点存入路径记录表的第一列
      % 构建解空间
      citys_index = 1:n;            %初始化城市索引数组，n：城市数量——27
      % 逐个蚂蚁路径选择
      for i = 1:m
          % 逐个城市路径选择，对于每只蚂蚁，逐个选择下一个要访问的城市，直到遍历完所有城市
         for j = 2:n
             tabu = Table(i,1:(j - 1));           % 获取当前蚂蚁已访问的城市列表(禁忌表)
             allow_index = ~ismember(citys_index,tabu); %获取当前蚂蚁可以访问的城市索引
             allow = citys_index(allow_index);    % 得到待访问的城市集合
             P = allow;
             % 计算城市间转移概率P，基于信息素浓度Tau和启发式信息Eta（如距离倒数）
             for k = 1:length(allow)
                 P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
             end
             P = P/sum(P);
             % 轮盘赌法选择下一个访问城市
             Pc = cumsum(P);            %计算累积概率  
            target_index = find(Pc >= rand); %轮盘赌法
            target = allow(target_index(1));
            Table(i,j) = target;        %更新蚂蚁的路径表。
         end
      end
      % 计算各个蚂蚁的路径距离Length
      Length = zeros(m,1);
      for i = 1:m
          Route = Table(i,:);
          for j = 1:(n - 1)
              Length(i) = Length(i) + D(Route(j),Route(j + 1));
          end
          Length(i) = Length(i) + D(Route(n),Route(1));
      end
      % 更新当前迭代中的最短路径、平均路径和最佳路径
      if iter == 1
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min_Length;  
          Length_ave(iter) = mean(Length);
          Route_best(iter,:) = Table(min_index,:);
      else
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min(Length_best(iter - 1),min_Length);
          Length_ave(iter) = mean(Length);
          if Length_best(iter) == min_Length
              Route_best(iter,:) = Table(min_index,:);
          else
              Route_best(iter,:) = Route_best((iter-1),:);
          end
      end
      % 更新信息素（初始化信息素增量矩阵）
      Delta_Tau = zeros(n,n);
      % 逐个蚂蚁计算（根据每只蚂蚁的路径长度更新信息素增量）
      for i = 1:m
          % 逐个城市计算
          for j = 1:(n - 1)
              Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
          end
          Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
      end
      Tau = (1-rho) * Tau + Delta_Tau;  %全局更新信息素浓度，其中rho是信息素蒸发率
    % 迭代次数加1，清空路径记录表

 %   figure;
 %最佳路径的迭代变化过程
    [Shortest_Length,index] = min(Length_best(1:iter));     %目前为止找到的最短路径的长度（一个值）和其索引
    Shortest_Route = Route_best(index,:);                   %根据索引index，从Route_best数组中提取出对应的最短路径（一个城市序列）
    plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
    [citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-'); %通过Shortest_Route索引从citys中选取路径上的城市坐标，并将路径的第一个城市和最后一个城市（即闭合路径的起点和终点）连接起来，形成一个闭环。o-指定点和线
    pause(0.3); %使程序暂停0.3秒，以便用户有时间观察绘制的路径
 
    iter = iter + 1;
    Table = zeros(m,n);

 % end
end

.mlx文件，该节输出：（共迭代100次，每次都会打印提示信息）

由于 pause(0.3)设置了0.3s的暂停，最后的matlab输出结果是视频形式的：

⑤最终结果输出

%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);

%% 绘图
figure(1)
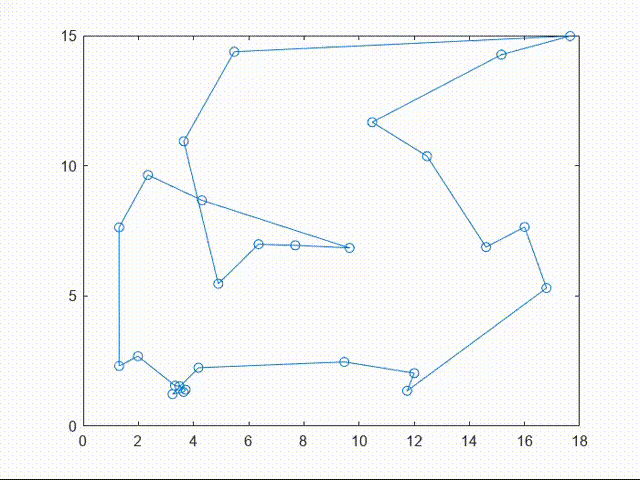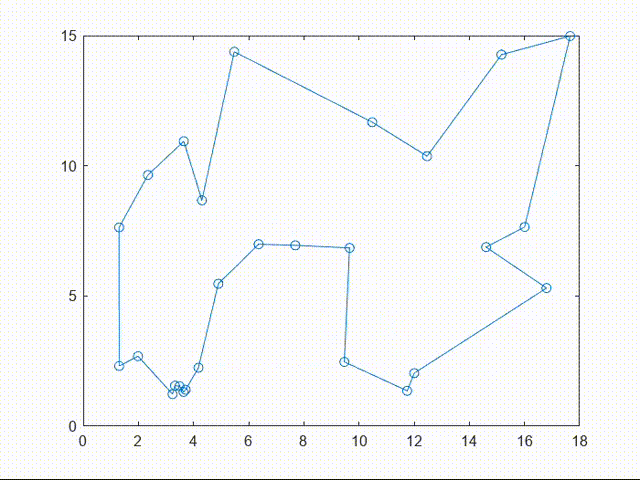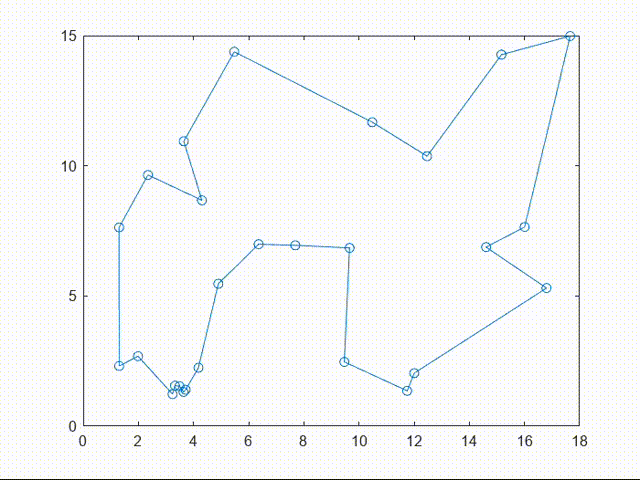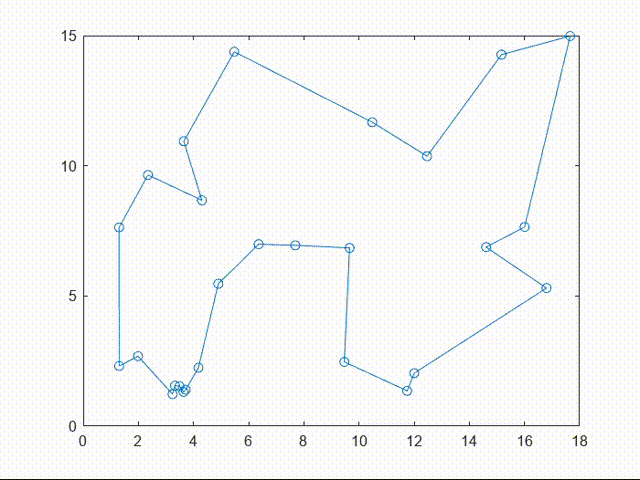
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
     [citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
    text(citys(i,1),citys(i,2),['   ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),'起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),'终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
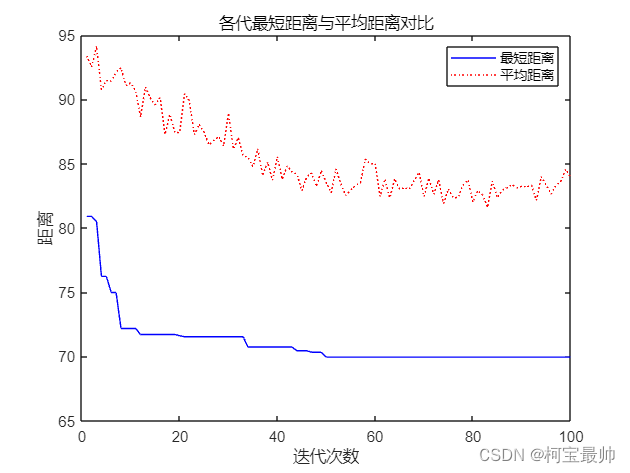
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')

输出得到的最短距离（一个值）和最短路径（城市号序列，按该序列号依次连接总路径最短）。

并输出随着迭代次数的增加，各代最短距离和平均距离的变化曲线。可见是不断优化的：

感谢你这么帅还关注柯宝！