题目

难度： 中等
题目内容：
给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。
示例1：

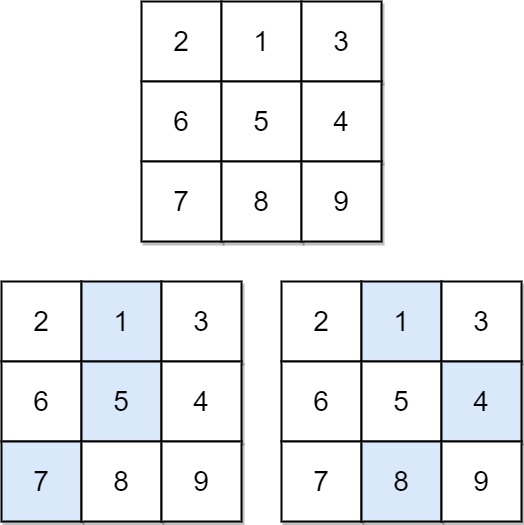
输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径

示例2：

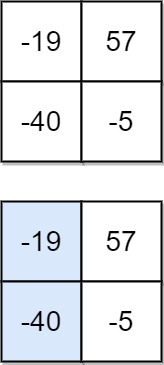
输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：如图所示，为和最小的下降路径

前置思路

该题的思路与上题几乎是完全一样的，只不过路径的选择加了一种，本质是一样的，且本题为矩阵，因此上下通路的复杂度应该是一样的。这里还是采用和上题一样的代码逻辑。

代码

class Solution:
    def minFallingPathSum(self, matrix: List[List[int]]) -> int:
        for i in range(1, len(matrix)):
            for j in range(len(matrix[i])):
                # 三种情况，两个边界+非边界
                if j == 0:
                    matrix[i][j] += min(matrix[i - 1][j], matrix[i - 1][j + 1])
                elif j == len(matrix[i]) - 1:
                    matrix[i][j] += min(matrix[i - 1][j], matrix[i - 1][j - 1])
                else:
                    matrix[i][j] += min(matrix[i - 1][j], matrix[i - 1][j - 1], matrix[i - 1][j + 1])
        return min(matrix[-1])

大神解

class Solution:
    def minFallingPathSum(self, matrix: List[List[int]]) -> int:
        n = len(matrix)
        # 存储结果
        f = [inf] + matrix[0] + [inf]
        # 从第二行开始遍历
        for i in range(1, n):
            # tmp用于记录上一行i-1的最小路径和
            tmp = inf
            # 依次更新每个位置的最小值
            for j in range(1, n+1):
                tmp ,f[j] = f[j], min(tmp, f[j], f[j+1]) + matrix[i][j-1]
        return min(f)

fine，总有更简单的方法，这里把判断条件都省了，但我感觉差不多，还是上面的代码更容易理解。

思考

莫得思考，个人感觉理解思路即可。