贪心算法终于有人讲明白了_【蓝桥杯贪心算法思想讲解以及代码实现】

文章目录

一、百度优解：

贪心算法（又称贪婪算法）是指：在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是某种意义上的局部最优解
贪心算法不是对所有问题都能得到整体的最优解，关键是贪心策略的选择

二、算法思路：

贪心算法一般按如下步骤进行：
（1）建立数学模型来描述问题。
（2）把求解的问题分成若干个子问题。
（3）对每个子问题求解，得到局部最优解。
（4）把子问题的解局部最优解合成原来解问题的一个解。
贪心算法是对一种对某些求最优解问题的更简单，更迅速的设计技术。贪心算法的特点是一步一步地进行，常以当前情况为基础根据某个优化测度作最优选择，而不考虑各种可能的整体情况，省去了为找最优解要穷尽所有可能而必须耗费大量的时间。贪心算法采用自顶向下，以迭代的方法做出相继的贪心选择，每做一次贪心选择，就将所求问题简化为一个规模更小的子问题，通过每一步贪心选择，可得到问题的一个最优解。虽然每一步上都要保证能获得局部最优解，但由此产生的全局解有时不一定是最优的，所以贪心算法不要回溯。

三、解题策略：

贪心算法不从整体最优上加以考虑，所做出的仅是在某种意义上的局部最优选择。使用贪心策略要注意局部最优与全局最优的关系，选择当前的局部最优并不一定能推导出问题的全局最优。贪心策略解题需要解决以下两个问题：
1、该问题是否适合使用贪心策略求解，也就是该问题是否具有贪心选择性质；
2、制定贪心策略，以达到问题的最优解或较优解。
要确定一个问题是否适合用贪心算法求解，必须证明每一步所作的贪心选择最终导致问题的整体最优解。证明的大致过程为：首先考察问题的一个整体最优解，并证明可修改这个最优解，使其以贪心选择开始，做了贪心选择后，原问题简化为规模更小的类似子问题。然后用数学归纳法证明通过每一步做贪心选择，最终可得到问题的整体最优解。

四、存在问题：

贪心算法也存在如下问题：
1、不能保证解是最佳的。因为贪心算法总是从局部出发，并没从整体考虑；
2、贪心算法一般用来解决求最大或最小解；
3、贪心算法只能确定某些问题的可行性范围。

五、应用实例：

例如，平时购物找零钱时，为使找回的零钱的硬币数最少，不要求找零钱的所有方案，而是从最大面值的币种开始，按递减的顺序考虑各面额，先尽量用大面值的面额，当不足大面值时才去考虑下一个较小面值，这就是贪心算法。

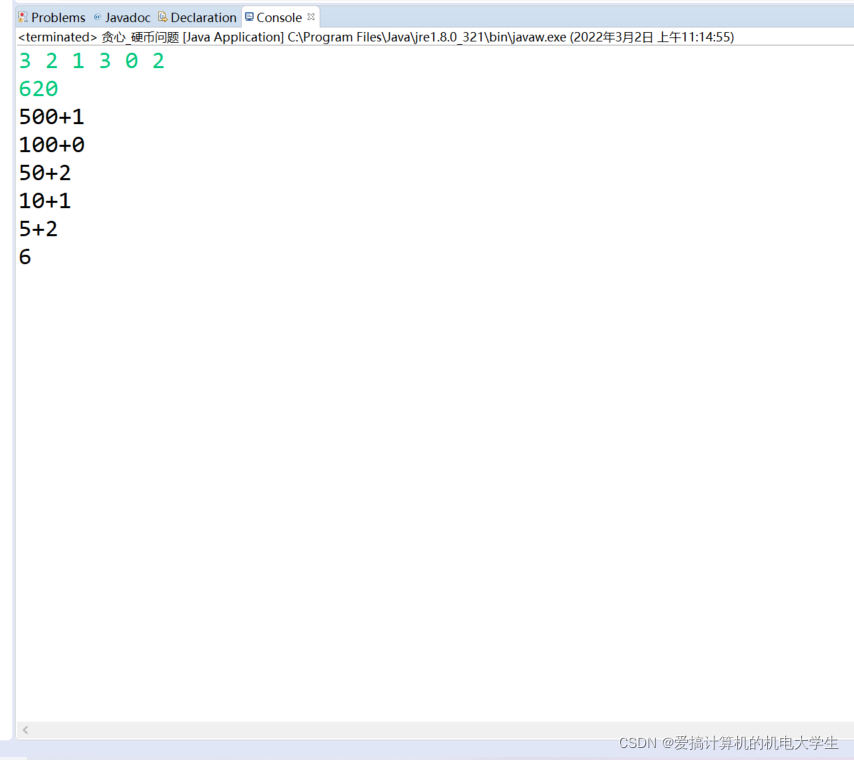
硬币支付问题：

输入 
3 2 1 3 0 2
输出
6

import java.util.Scanner;

public class 贪心_硬币问题 {
	static int[] cnt = new int[6];//用来存储各个硬币的数量
	static int[] count = {1,5,10,50,100,500};

	public static void main(String[] args) {
		Scanner sc =new Scanner(System.in);
		String nextLine = sc.nextLine();
		String[] split = nextLine.split(" ");
		for(int i = 0;i<split.length;i++) {//先将硬币的数量添加至cnt中
			cnt[i] = Integer.parseInt(split[i]);
		}
		int sum = sc.nextInt();//获取要结账的金额
		int result = f(sum,5);
		System.out.println(result);
	}
	public static int f(int A,int cur) {
		if(A<=0) return 0;
		if(cur==0) return A;
		int value = count[cur];
		int c = A/value;
		int shu = cnt[cur];
		int t = min(shu,c);
		System.out.println(value+"+"+t);
		return t+f(A-t*count[cur],cur-1);
	}
	public static int min(int a,int b) {
		return a<b?a:b;
	}
}

运行结果：
在这里插入图片描述

快速渡河问题：

题目：大概就是讲一群人渡河的问题，只有一艘船，该船只能乘坐两人，由于每个人的重量不一样，渡河的速度也就不一样，两个不同重量的人渡船，则以较慢的为准，求最终全部人都度过去的时间；
一般思路：就是速度快的来回送，但是这不是最优解；
正确思路：先是两个最快的过去（s1中第一个就是代表这个）然后最快的回来（s1中第二个就是代表这个），第二趟就是两个最慢的过去（第三个），我刚刚在终点等待的较快的把船开回来，这样子总体的速度就会快很多。
还没看懂同学可以联系代码，用手绘制一下哈，


import java.util.Scanner;

public class 贪心_快速渡河 {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int count = sc.nextInt();
		sc.nextLine();
		String speeds = sc.nextLine();
		String[] split = speeds.split(" ");
		int[] arr = new int[split.length];
		for(int i = 0;i<split.length;i++) {
			arr[i] = Integer.parseInt(split[i]);
		}
		f(count,arr);
	}
	public static void f(int n,int[] speed) {
		int left = n;
		int ans = 0;
		while(left>0) {
			if(left == 1) {
				ans +=speed[0];
				break;
			}
			else if(left == 2) {
				ans+=speed[1];
				break;
			}
			else if(left == 3) {
				ans +=speed[2]+speed[0]+speed[1];
				break;
			}else {
				int s1 = speed[1]+speed[0]+speed[left-1]+speed[1];
				int s2 = speed[left-1]+speed[left-2]+2*speed[0];
				int t = Math.min(s1,s2);
				left-=2;
				ans+=t;
			}
		}
		System.out.println(ans);
	}
}

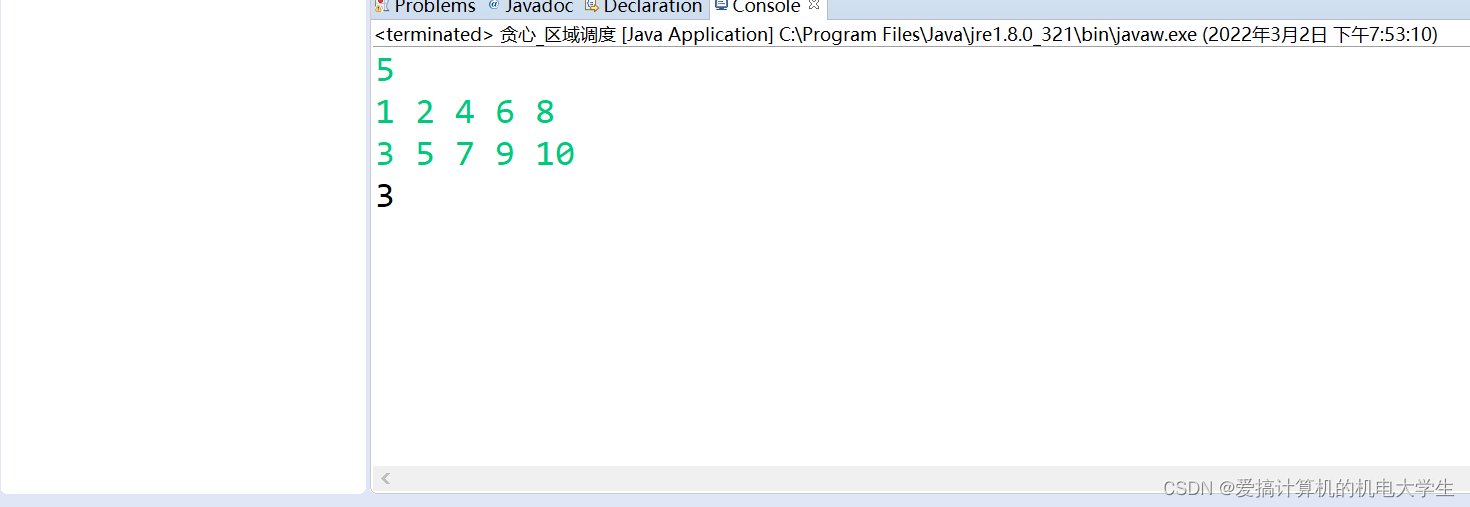
区间调度问题


import java.util.Scanner;

//（1）首先自己先创建一个对象，用来存储区域，
//（2）创建的对象有两个特性，一个是记录区间的起点，一个是记录区间终点
//（3）创建一个该对象的数组，自定义comparable方法，以终点为比较第一要素；
//注意：如果采用起点来作为比较对象的话，我们所能够得到的区间的数量并不是最多的，
//（4）先获取第一个终点的值；然后比较那个是离这个终点最近的起点；（由于这个数组是经过排序的，所以不必担心他的长度会过长）
//（5）获取这个起点的终点，将这个终点作为y再进行比较；
public class 贪心_区域调度 {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int[] s = new int[n];
		int[] t = new int[n];
		for(int i = 0;i<n;i++) {
			s[i] = sc.nextInt();
		}
		for(int j = 0;j<n;j++) {
			t[j] = sc.nextInt();
		}
		Job[] job = new Job[n];
		for(int k = 0;k<n;k++) {
			job[k] = new Job(s[k],t[k]);
		}
		f(n,job);
	}
	public static void f(int n,Job[] job) {
		int cnt = 1;
		int y = job[0].t;
		for(int i = 0;i<n;i++) {
			if(job[i].s>y) {
				cnt++;
				y = job[i].t;
			}
		}
		System.out.println(cnt);
	}
	private static class Job implements Comparable<Job> {
		int s;
		int t;
		public Job(int s,int t){
			this.s = s;
			this.t = t;
		}
		@Override
		public int compareTo(Job other) {
			// TODO Auto-generated method stub
			int x = this.t-other.t;
			if(x == 0)return this.s-other.s;
			else return x;
		}
		
	}
}

在这里插入图片描述

区间选点问题：


import java.util.Arrays;
import java.util.Scanner;

//首先创建一个类，该类有三个属性，起点，终点，数量
//创建该类的数组，读取键盘数据来创建对象，
//获取数组的最后一位的终点，创建最大值，同时一个等大的数组，用来标识已选的点
//遍历该类的数组，找到该区间内以标识多少个点，
//根据目前的区间需要的标识的点的数量减去已经标识的数量，从右往左依次标识，直至需要标识的数量为0为止


public class 贪心_区域选点 {
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		Util[] utils = new Util[n];
		for(int i = 0;i<n;i++) {
			 utils[i] = new Util(sc.nextInt(),sc.nextInt(),sc.nextInt());
		}
		Arrays.sort(utils);
		int max = utils[n-1].t;
		int[] arr = new int[max+1];
		
		for(int i = 0;i<n;i++) {
			int s = utils[i].s;
			int t = utils[i].t;
			int count = utils[i].c;
			int cnt = find(arr,s,t);
			int newcount = count-cnt;
			while(newcount>0) {
				if(arr[t]==0) {
					arr[t] = 1;
					newcount--;
					t--;
				}else {
					t--;
				}
			}
			
		}
		int find = find(arr,0,max);
		System.out.println(find);
	}
	public static int find(int[] arr,int s,int t) {
		int count =  0;
		for(int i = s;i<=t;i++) {
			if(arr[i] != 0) {
				count++;
			}
		}
		return count;
	}
	private static class Util implements Comparable<Util>{
		int s;
		int t;
		int c;
		public Util(int s,int t,int c) {
			this.s = s;
			this.t = t;
			this.c = c;
		}
		@Override
		public int compareTo(Util o) {
			// TODO Auto-generated method stub
			int x = this.t-o.t;
			if(x==0) return this.c-o.c;
			else return x;
		}
		
	}
}

区域覆盖问题：


import java.util.Scanner;

//（1）创建一个类，含有两个属性，起点和终点，该类是按照起点进行排序得到
//（2）获取键盘输入的数据，进行排序
//（3）选取start，只要起点满足大于start即可，依次遍历获取在该条件下最右的点
//（4）然后将这个最右的点赋值给start，计数++，直到最右的点大于区间的终点
//（5） 注意：如果没有大于则返回-1，
public class 贪心_区间覆盖 {
	public static void main(String[] args) {
		
	}
	private static class demo implements Comparable<demo>{
		int s;
		int t;
		public demo(int s,int t) {
			this.s = s;
			this.t = t;
		}
		@Override
		public int compareTo(demo o) {
			int x = this.s - o.s;
			if(x==0)return this.t-o.t;
			// TODO Auto-generated method stub
			return x;
		}
		
	}
}