Tips:本篇blog适合刚开始学习数论部分的同学
本题解仅代表个人思路,如有异议欢迎批评指正,谢谢
一. 概述
该章节讲述的是矩阵运算及快速幂的概念,学过的同学可以跳过本章,直接看矩阵快速幂
1.矩阵
矩阵类似于向量,我们可以这么来表示一个矩阵
如上图,表示了一个 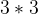
矩阵也有加减和乘法运算(请注意矩阵没有除法运算),并且这些运算都是矩阵之间的,即可以矩阵加矩阵但不能矩阵加数字
2.矩阵加减
矩阵的加减运算时,只有两个同型矩阵(即行列数相同)才能进行加减运算,两个矩阵相同位置上的数做加减运算,最终会得到一个矩阵,就是运算结果,例如
可以看出,矩阵的加减法是具有交换律和结合律的。
3.矩阵乘法
矩阵乘法与加减法略有不同,矩阵进行乘法运算时,不一定两个矩阵是同型的(即不一定行列数相同),矩阵乘法的计算方法为
设 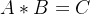
我们举个形象的例子
到这里应该很清楚了,所以可以看出,矩阵乘法满足结合律,但不满足交换律
4.快速幂
快速幂可以加速幂运算,试想一下,如果我们直接枚举来进行幂运算,时间复杂度是 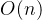
我们可以用快速幂来优化这一过程,我们用类似二进制分解的原理,利用位运算来加速,最终的时间复杂度可以达到 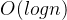
具体的代码实现是这样滴
long long qpow(long long x,long long y)
{
long long ans = 1;
while (y)
{
if (y & 1) ans = (ans * x) % mod;//mod是模数
x = (x * x) % mod;
y >>= 1;
}
return ans;
}二. 矩阵快速幂
1.引入
很多递推的题目,需要我们来递推求解状态,这时候的复杂度一般是 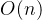

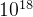
例如下面这道题目
斐波那契数列 - 洛谷
2.思路
这一题中,
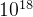
如何进行求解呢?
我们知道,设斐波那契数列为 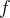

我们尝试把这个递推式放到矩阵里,就变成了这个样子:
大家不妨代入一下试一试。
所以这个式子里,最后一个矩阵是如何推出来的呢?
我们可以用列表法来推出最后一个矩阵,我们以后计算的就是这个矩阵的幂。
| 矩阵 |  |  |
 | 1 | 1 |
 | 1 | 0 |
可以发现,我们只要让表中每一行值为1所对应的值加在一起等于这一行代表的值即可。
接下来,我们考虑如何用矩阵快速幂来求解。
可以发现,把上面的矩阵乘法求斐波那契数列的式子不断展开,就会变成这个样子:
其中矩阵的幂次取决于你是从哪一个值开始递推,如果从 
所以,我们用求解快速幂的方法带入到矩阵中,再模拟矩阵乘法,就可以用 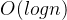
3. 代码实现
要注意的是,矩阵 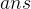
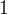
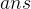
大家可以尝试一下,很容易发现这个道理。
#include <bits/stdc++.h>
using namespace std;
long long n;
const int mod = 1e9+7; //模数
struct A //结构体存矩阵
{
long long a[3][3];
};
A multi(A a,A b) //模拟矩阵乘法
{
A ans;
for (int i=1;i<=2;i++)
{
for (int j=1;j<=2;j++)
{
ans.a[i][j] = 0;
for (int k=1;k<=2;k++)
{
ans.a[i][j] = (ans.a[i][j]+a.a[i][k]*b.a[k][j])%mod;
ans.a[i][j] %= mod;
}
}
}
return ans;
}
long long qpows(long long b)
{
A ans,a;
a.a[1][1] = 1; //初始化斐波那契
a.a[1][2] = 1;
a.a[2][1] = 1;
a.a[2][2] = 0;
ans.a[1][1] = 1; //初始化答案矩阵
ans.a[1][2] = 0;
ans.a[2][1] = 0;
ans.a[2][2] = 1;
while (b) //快速幂
{
if (b & 1) ans = multi(ans,a);
a = multi(a,a);
b >>= 1;
}
return ans.a[1][1]%mod;
}
int main()
{
cin >> n;
if (n <= 2) //特判
{
cout<<1;
return 0;
}
cout<<qpows(n-1);
return 0;
}
三. 结语
矩阵快速幂的应用范围相当广泛,当我们需要优化递推或动态规划时,往往会考虑使用矩阵快速幂,大家可以再去练习一下 广义斐波那契数列 - 洛谷 来巩固所学内容。
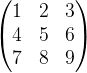
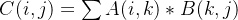

![[f_i,f_{i-1}] = [f_{i-1},f_{i-2}] * \begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJmX2klMkNmXyU3QmktMSU3RCU1RCUyMCUzRCUyMCU1QmZfJTdCaS0xJTdEJTJDZl8lN0JpLTIlN0QlNUQlMjAqJTIwJTVDYmVnaW4lN0JibWF0cml4JTdEJTIwMSUyMCUyNiUyMDElNUMlNUMlMjAxJTIwJTI2JTIwMCUyMCU1Q2VuZCU3QmJtYXRyaXglN0Q%3D)
![[f_i,f_{i-1}] = [f_{1},f_{2}] * \begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}^{n-2}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJmX2klMkNmXyU3QmktMSU3RCU1RCUyMCUzRCUyMCU1QmZfJTdCMSU3RCUyQ2ZfJTdCMiU3RCU1RCUyMColMjAlNUNiZWdpbiU3QmJtYXRyaXglN0QlMjAxJTIwJTI2JTIwMSU1QyU1QyUyMDElMjAlMjYlMjAwJTIwJTVDZW5kJTdCYm1hdHJpeCU3RCU1RSU3Qm4tMiU3RA%3D%3D)
![[f_i,f_{i-1}] = [f_{0},f_{1}] * \begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}^{n-1}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJmX2klMkNmXyU3QmktMSU3RCU1RCUyMCUzRCUyMCU1QmZfJTdCMCU3RCUyQ2ZfJTdCMSU3RCU1RCUyMColMjAlNUNiZWdpbiU3QmJtYXRyaXglN0QlMjAxJTIwJTI2JTIwMSU1QyU1QyUyMDElMjAlMjYlMjAwJTIwJTVDZW5kJTdCYm1hdHJpeCU3RCU1RSU3Qm4tMSU3RA%3D%3D)