命名实体识别BiLSTM-CRF – 潘登同学的NLP笔记
文章目录
标注策略
IOB 比如识别人名:PER
B:begin表示人名起始点O:out表示非人名I:internal表示人名,但不是起始点(中部或者结尾点)
BMES 比如识别人名: PER
B:begin表示人名起始点M:middle表示人名中部S: single表示非人名E:end表示人名结束点
早期方法
是基于规则与词典的方式, 就是把所有词记录下来, 再用词典去匹配文章…
- 优点: 准
- 缺点: 泛化能力不好
基于统计学习的方法
- HMM\CRF(jieba分词器)
- 混合方法
- 统计学习方法之间或内部层叠融合(集成学习)
- 规则、词典和机器学习方法之间的融合
- 将各类模型、算法结合起来,将前一级模型的结果作为下一级的训练数据(stacking)
深度学习方法
- NN/CNN-CRF
- RNN-CRF/LSTM-CRF
- 注意力机制
- 迁移学习(BERT-BiLSTM-CRF)
BiLSTM-CRF
普通的BiLSTM最后接的的一个softmax层, 在处理序列标注问题的时候, softmax也没考虑到序列结果,如连续出现两个动词,在一句话中是不太可能的; 所以后面接一层CRF,CRF是使得最终的出现的结果序列Loss最小,从而能应用于序列标注问题上
- 生成式模型: (统计学习方法,计算(联合)概率分布的参数,不一定要x,y,有的话更好) HMM GMM Naive-bayes
- 判别式模型: (有判别式的,计算P(y|x)需要x,y来训练计算) CRF DT LR NN
我们假设我们有一个数据集有两类实体类型,Person 和 Organization。因此事实上在我们的数据集中,我们有 5 个实体标签:
- B-Person
- I- Person
- B-Organization
- I-Organization
- O
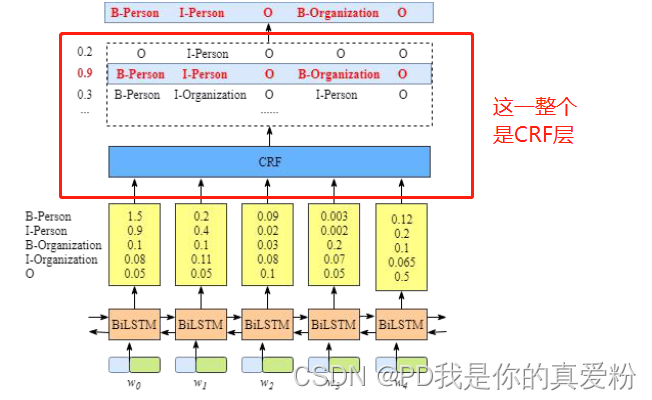
进而,x 是一个句子包含 5 个词, w 0 , w 1 , w 2 , w 3 , w 4 w_0,w_1,w_2,w_3,w_4 w0,w1,w2,w3,w4。更多地,在句子 x, [ w 0 , w 1 ] [w_0,w_1] [w0,w1] 是一个 Person entity, [ w 3 ] [w_3] [w3] 是一个 Organization entity 和其它的是“O”
- 首先, 在句子每个词,x 被表达为一个向量,向量由包含词的字嵌入和词嵌入组成。字的嵌入是随机初始化的。词嵌入通常是来自于预训练的词嵌入模型文件。在整个训练过程中所有的嵌入将会被细粒度的调优。
- 其次, BiLSTM-CRF 模型的输入是那些嵌入向量,输出是对于句子 x 中词的预测标签
- BiLSTM层的输出是一个类别的logist(就是softmax之间的Z),然后输入CRF层,CRF根据所有输入的Z,计算一条最有可能的路径(类似于维特比算法计算条件概率最大的那条路径),最后得到一整段输出
如果不加CRF层
很明显,I-Organization I-Person和I-Organization I-Person这些输出是无效的。
CRF 层可以从训练数据学习限制
CRF 层可以加一些限制给最后的预测标签去确保它们是有效的。这些限制通过训练过程可以被 CRF 层从训练集数据中自动学到, 这些限制可以是
- 句子开头首个词的标签应该是
B-或O, 而不是I- B-label1 I-label2 I-label3 I-..., 在这个模式中, label1, label2, label3 … 应该是同样的命名实体标签 . 例如 ,B-Person I-Person是有效的 , 但B-Person I-Organization是无效的;
有了这些有用的限制,无效的预测标签序列的数量会急剧的下降
CRF层
在 CRF 层的损失函数中,我们有两种类型的分数。这两分数是 CRF 层的关键;
Emission score(发射分数)
第一个是 emission score。这些 emission scores 来自于 BiLSTM 层(就是前面说的 Z Z Z)
我们使用 x i , x j x_i,x_j xi,xj 去表达一个 emission score。 i i i 是词的索引同时 j j j 是标签的索引。例如,根据图, ( x i = 1 , x j = 2 ) = ( x w 1 , x B − O r g a n i z a t i o n ) = 0.1 (x_i=1,x_j=2) = (x_{w1},x_{B-Organization})=0.1 (xi=1,xj=2)=(xw1,xB−Organization)=0.1 这意味着 w1 作为 B-Organization 的分数是 0.1
Transition score(转移分数)
我们使用 ( y i , y j ) (y_i,y_j) (yi,yj) 去表达一个 transition score。例如, (y_{B-Person},y_{I-Person})=0.9$ 意味着标签转移B−Person→I−Person 的分数是 0.9。因此, 我们有一个转移分数矩阵存储了所有的标签和标签之间的分数;
为了去使得转移分数矩阵更加的鲁棒,我们将多添加两个标签 START 和 END。START 意味着句子的开始,不是第一个词。END 意味着句子的结束。
举个例子
| START | B-Person | I-Person | B-Organization | I-Organization | O | END | |
|---|---|---|---|---|---|---|---|
| START | 0 | 0.8 | 0.007 | 0.7 | 0.0008 | 0.9 | 0.08 |
| B-Person | 0 | 0.6 | 0.9 | 0.2 | 0.0006 | 0.6 | 0.009 |
| I-Person | -1 | 0.5 | 0.53 | 0.55 | 0.0003 | 0.85 | 0.008 |
| B-Organization | 0.9 | 0.5 | 0.0003 | 0.25 | 0.8 | 0.77 | 0.006 |
| I-Organization | 0 | 0.8 | 0.007 | 0.7 | 0.65 | 0.76 | 0.2 |
| O | 0 | 0.65 | 0.0007 | 0.7 | 0.0008 | 0.9 | 0.08 |
| END | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
事实上,这个矩阵是 BiLSTM-CRF 模型的参数。在你训练这个模型之前,你可以随机初始化矩阵中的所有转移分数。在模型的训练过程中所有随机的分数将会被自动地更新。换句话说, CRF 层可以由它自己学习那些限制。我们没有必要去手动建立这个矩阵。这些分数随着训练迭代的增加会逐渐变得越来越合理;
Loss函数
CRF 的损失函数,它由真正路径的分数和所有可能路径的总分数构成;
我们也有一个含有 5 个单词的句子。这些可能的路径将会是:
- START B-Person B-Person B-Person B-Person B-Person END
- START B-Person I-Person B-Person B-Person B-Person END
- …
- START B-Person I-Person O B-Organization O END
- …
- O O O O O O O
假设每一个可能的路径有一个分数
P
i
P_i
Pi,并且这里总共有 N 种可能的路径, 这些路径的
总分数是
P
t
o
t
a
l
=
P
1
+
P
2
+
⋯
+
P
N
=
e
S
1
+
e
S
2
+
…
+
e
S
N
P_{total} = P_1 + P_2 + \cdots + P_N = e^{S_1} + e^{S_2} + \ldots + e^{S_N}
Ptotal=P1+P2+⋯+PN=eS1+eS2+…+eSN
其中,
S
i
S_i
Si可以理解为一个路径的分数,
S
i
S_i
Si 由两部分组成
S
i
=
E
m
i
s
s
i
o
n
S
c
o
r
e
+
T
r
a
n
s
i
t
i
o
n
S
c
o
r
e
S_i=EmissionScore+TransitionScore
Si=EmissionScore+TransitionScore (之所以用e,是与softmax类似)
P
i
=
e
Z
i
e
Z
1
+
e
Z
2
+
⋯
+
e
Z
k
P_i = \frac{e^{Z_i}}{e^{Z_1} + e^{Z_2} + \cdots + e^{Z_k}}
Pi=eZ1+eZ2+⋯+eZkeZi
如果我们说
1
0
t
h
10^{th}
10th 路径是真实的标签路径, 换句话说, the
1
0
t
h
10^{th}
10th path 是由训练集提供的标签。分数
P
10
P_{10}
P10 它就应该是在所有可能路径中有最大比例的。下面给出的式子同时也是损失函数,在训练过程中,我们 BiLSTM-CRF 模型的参数值将会被不断的更新,为了保障真实路径的分数所占比例不断的增加。
L
o
s
s
=
−
P
R
e
a
l
P
a
t
h
P
1
+
P
2
+
…
+
P
N
Loss = -\frac{P_{Real Path}}{P_1 + P_2 + \ldots + P_N}
Loss=−P1+P2+…+PNPRealPath
以START B-Person I-Person O B-Organization O END为例,
E
m
i
s
s
i
o
n
S
c
o
r
e
=
x
0
,
S
T
A
R
T
+
x
1
,
B
−
P
e
r
s
o
n
+
x
2
,
I
−
P
e
r
s
o
n
+
x
3
,
O
+
x
4
,
B
−
O
r
g
a
n
i
z
a
t
i
o
n
+
x
5
,
O
+
x
6
,
E
N
D
T
r
a
n
s
i
t
i
o
n
S
c
o
r
e
=
t
S
T
A
R
T
,
B
−
P
e
r
s
o
n
+
t
B
−
P
e
r
s
o
n
,
I
−
P
e
r
s
o
n
+
t
I
−
P
e
r
s
o
n
,
O
+
t
O
,
B
−
O
r
g
a
n
i
z
a
t
i
o
n
+
t
B
−
O
r
g
a
n
i
z
a
t
i
o
n
,
E
N
D
EmissionScore = x_{0,START} + x_{1,B-Person} + x_{2,I-Person} + x_{3,O} + x_{4,B-Organization} + x_{5,O} + x_{6,END} \\ TransitionScore = t_{START,B-Person} + t_{B-Person,I-Person} + t_{I-Person,O} + t_{O,B-Organization} + t_{B-Organization,END} \\
EmissionScore=x0,START+x1,B−Person+x2,I−Person+x3,O+x4,B−Organization+x5,O+x6,ENDTransitionScore=tSTART,B−Person+tB−Person,I−Person+tI−Person,O+tO,B−Organization+tB−Organization,END
对Loss函数取对数
L
o
g
L
o
s
s
F
u
n
c
t
i
o
n
=
−
l
o
g
P
R
e
a
l
P
a
t
h
P
1
+
P
2
+
…
+
P
N
=
−
l
o
g
e
S
R
e
a
l
P
a
t
h
e
S
1
+
e
S
2
+
…
+
e
S
N
=
−
(
l
o
g
(
e
S
R
e
a
l
P
a
t
h
)
−
l
o
g
(
e
S
1
+
e
S
2
+
…
+
e
S
N
)
)
=
−
(
S
R
e
a
l
P
a
t
h
−
l
o
g
(
e
S
1
+
e
S
2
+
…
+
e
S
N
)
)
\begin{aligned} LogLossFunction &= -log\frac{P_{RealPath}}{P_1 + P_2 + \ldots + P_N} \\ &= -log\frac{e^{S_{RealPath}}}{e^{S_1} + e^{S_2} + \ldots + e^{S_N}} \\ &= -(log(e^{S_{RealPath}}) - log(e^{S_1} + e^{S_2} + \ldots + e^{S_N})) \\ &= -(S_{RealPath} - log(e^{S_1} + e^{S_2} + \ldots + e^{S_N})) \\ \end{aligned}
LogLossFunction=−logP1+P2+…+PNPRealPath=−logeS1+eS2+…+eSNeSRealPath=−(log(eSRealPath)−log(eS1+eS2+…+eSN))=−(SRealPath−log(eS1+eS2+…+eSN))
S
R
e
a
l
P
a
t
h
S_{RealPath}
SRealPath的计算方法已知,关键是怎么计算
l
o
g
(
e
S
1
+
e
S
2
+
…
+
e
S
N
)
log(e^{S_1} + e^{S_2} + \ldots + e^{S_N})
log(eS1+eS2+…+eSN)
训练阶段-动态规划
目标: l o g ( e S 1 + e S 2 + … + e S N ) log(e^{S_1} + e^{S_2} + \ldots + e^{S_N}) log(eS1+eS2+…+eSN)
这是过程是一个分数的累加。思想类似于动态规划,为了简化,我们假设句子长度为3,标签数量为2
Emission scores
| l 1 l_1 l1 | l 2 l_2 l2 | |
|---|---|---|
| w 0 w_0 w0 | x 0 , 1 x_{0,1} x0,1 | x 0 , 2 x_{0,2} x0,2 |
| w 1 w_1 w1 | x 1 , 1 x_{1,1} x1,1 | x 1 , 2 x_{1,2} x1,2 |
| w 2 w_2 w2 | x 2 , 1 x_{2,1} x2,1 | x 2 , 2 x_{2,2} x2,2 |
Transition scores
| l 1 l_1 l1 | l 2 l_2 l2 | |
|---|---|---|
| l 1 l_1 l1 | t 0 , 1 t_{0,1} t0,1 | t 0 , 2 t_{0,2} t0,2 |
| l 2 l_2 l2 | t 1 , 1 t_{1,1} t1,1 | t 1 , 2 t_{1,2} t1,2 |
- 第一个单词 W 0 W_0 W0
O b s = [ x 0 , 1 , x 0 , 2 ] , p r e v i o u s = N o n e Obs = [x_{0,1},x_{0,2}],previous=None Obs=[x0,1,x0,2],previous=None
在第一个单词,我们没有之前的结果,因此previous是空,另外,我们只能观测第一个单词的发射分数是
O
b
s
=
[
x
0
,
1
,
x
0
,
2
]
Obs = [x_{0,1},x_{0,2}]
Obs=[x0,1,x0,2],此时
W
0
W_0
W0的所有路径的总分数
T
o
t
a
l
S
c
o
r
e
(
w
0
)
=
l
o
g
(
e
x
0
,
1
+
e
x
0
,
2
)
TotalScore(w_0) = log(e^{x_{0,1}} + e^{x_{0,2}})
TotalScore(w0)=log(ex0,1+ex0,2)
更新 p r e v i o u s = [ l o g ( e x 0 , 1 ) , l o g ( e x 0 , 2 ) ] previous = [log(e^{x_{0,1}}),log(e^{x_{0,2}})] previous=[log(ex0,1),log(ex0,2)]
- 第二个单词 W 1 W_1 W1
O b s = [ x 1 , 1 , x 1 , 2 ] , p r e v i o u s = [ x 0 , 1 , x 0 , 2 ] Obs = [x_{1,1},x_{1,2}],previous=[x_{0,1},x_{0,2}] Obs=[x1,1,x1,2],previous=[x0,1,x0,2](Obs与previous的长度始终等于标签数量)
扩展previous为
p
r
e
v
i
o
u
s
=
(
x
0
,
1
x
0
,
1
x
0
,
2
x
0
,
2
)
previous = \begin{pmatrix} x_{0,1} & x_{0,1} \\ x_{0,2} & x_{0,2} \\ \end{pmatrix}
previous=(x0,1x0,2x0,1x0,2)
扩展Obs为
O
b
s
=
(
x
1
,
1
x
1
,
2
x
1
,
1
x
1
,
2
)
Obs = \begin{pmatrix} x_{1,1} & x_{1,2} \\ x_{1,1} & x_{1,2} \\ \end{pmatrix}
Obs=(x1,1x1,1x1,2x1,2)
加和previous,obs和transition scores
s
c
o
r
e
s
=
(
x
0
,
1
x
0
,
1
x
0
,
2
x
0
,
2
)
+
(
x
1
,
1
x
1
,
2
x
1
,
1
x
1
,
2
)
+
(
t
1
,
1
t
1
,
2
t
2
,
1
t
2
,
2
)
=
(
x
0
,
1
+
x
1
,
1
+
t
1
,
1
x
0
,
1
+
x
1
,
2
+
t
1
,
2
x
0
,
2
+
x
1
,
1
+
t
2
,
1
x
0
,
2
+
x
1
,
2
+
t
2
,
2
)
scores = \begin{pmatrix} x_{0,1} & x_{0,1} \\ x_{0,2} & x_{0,2} \\ \end{pmatrix} + \begin{pmatrix} x_{1,1} & x_{1,2} \\ x_{1,1} & x_{1,2} \\ \end{pmatrix} + \begin{pmatrix} t_{1,1} & t_{1,2} \\ t_{2,1} & t_{2,2} \\ \end{pmatrix} = \begin{pmatrix} x_{0,1} + x_{1,1} + t_{1,1} & x_{0,1} + x_{1,2} + t_{1,2} \\ x_{0,2} + x_{1,1} + t_{2,1} & x_{0,2} + x_{1,2} + t_{2,2} \\ \end{pmatrix}
scores=(x0,1x0,2x0,1x0,2)+(x1,1x1,1x1,2x1,2)+(t1,1t2,1t1,2t2,2)=(x0,1+x1,1+t1,1x0,2+x1,1+t2,1x0,1+x1,2+t1,2x0,2+x1,2+t2,2)
transition scores是转移分数,所以前面两个矩阵的第二个下标,要与transition scores的下标对上,第一个矩阵中元素的第二个下标,是transition scores中的第一个下标; 第二个矩阵中元素的第二个下标,是transition scores中的第二个下标
更新 p r e v i o u s = [ l o g ( e x 0 , 1 + x 1 , 1 + t 1 , 1 + e x 0 , 2 + x 1 , 1 + t 2 , 1 ) , l o g ( e x 0 , 1 + x 1 , 2 + t 1 , 2 + e x 0 , 2 + x 1 , 2 + t 2 , 2 ) ] previous = [log(e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}}),log(e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}})] previous=[log(ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1),log(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2)]
计算总分数
T
o
t
a
l
S
c
o
r
e
(
w
0
→
w
1
)
=
l
o
g
(
e
p
r
e
v
i
o
u
s
[
0
]
+
e
p
r
e
v
i
o
u
s
[
1
]
)
=
l
o
g
(
e
l
o
g
(
e
x
0
,
1
+
x
1
,
1
+
t
1
,
1
+
e
x
0
,
2
+
x
1
,
1
+
t
2
,
1
)
+
e
l
o
g
(
e
x
0
,
1
+
x
1
,
2
+
t
1
,
2
+
e
x
0
,
2
+
x
1
,
2
+
t
2
,
2
)
)
=
l
o
g
(
e
x
0
,
1
+
x
1
,
1
+
t
1
,
1
+
e
x
0
,
2
+
x
1
,
1
+
t
2
,
1
+
e
x
0
,
1
+
x
1
,
2
+
t
1
,
2
+
e
x
0
,
2
+
x
1
,
2
+
t
2
,
2
)
\begin{aligned} TotalScore(w_0 \to w_1) &= log(e^{previous[0]} + e^{previous[1]}) \\ &= log(e^{log(e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}})} + e^{log(e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}})}) \\ &= log(e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}} + e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}})\\ \end{aligned}
TotalScore(w0→w1)=log(eprevious[0]+eprevious[1])=log(elog(ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1)+elog(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2))=log(ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1+ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2)
上面这个式子就是我们的目标 l o g ( e S 1 + e S 2 + … + e S N ) log(e^{S_1} + e^{S_2} + \ldots + e^{S_N}) log(eS1+eS2+…+eSN)的一个具体表述了,更一般的我们再推一步
- 第三个单词 W 2 W_2 W2
O b s = [ x 2 , 1 , x 2 , 2 ] , p r e v i o u s = [ l o g ( e x 0 , 1 + x 1 , 1 + t 1 , 1 + e x 0 , 2 + x 1 , 1 + t 2 , 1 ) , l o g ( e x 0 , 1 + x 1 , 2 + t 1 , 2 + e x 0 , 2 + x 1 , 2 + t 2 , 2 ) ] Obs = [x_{2,1},x_{2,2}],previous=[log(e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}}),log(e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}})] Obs=[x2,1,x2,2],previous=[log(ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1),log(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2)]
扩展previous为
p
r
e
v
i
o
u
s
=
(
l
o
g
(
e
x
0
,
1
+
x
1
,
1
+
t
1
,
1
+
e
x
0
,
2
+
x
1
,
1
+
t
2
,
1
)
l
o
g
(
e
x
0
,
1
+
x
1
,
1
+
t
1
,
1
+
e
x
0
,
2
+
x
1
,
1
+
t
2
,
1
)
l
o
g
(
e
x
0
,
1
+
x
1
,
2
+
t
1
,
2
+
e
x
0
,
2
+
x
1
,
2
+
t
2
,
2
)
l
o
g
(
e
x
0
,
1
+
x
1
,
2
+
t
1
,
2
+
e
x
0
,
2
+
x
1
,
2
+
t
2
,
2
)
)
previous = \begin{pmatrix} log(e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}}) & log(e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}}) \\ log(e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}}) & log(e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}}) \\ \end{pmatrix}
previous=(log(ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1)log(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2)log(ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1)log(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2))
扩展Obs为
O
b
s
=
(
x
2
,
1
x
2
,
2
x
2
,
1
x
2
,
2
)
Obs = \begin{pmatrix} x_{2,1} & x_{2,2} \\ x_{2,1} & x_{2,2} \\ \end{pmatrix}
Obs=(x2,1x2,1x2,2x2,2)
加和previous,obs和transition scores
s
c
o
r
e
s
=
(
l
o
g
(
e
x
0
,
1
+
x
1
,
1
+
t
1
,
1
+
e
x
0
,
2
+
x
1
,
1
+
t
2
,
1
)
l
o
g
(
e
x
0
,
1
+
x
1
,
1
+
t
1
,
1
+
e
x
0
,
2
+
x
1
,
1
+
t
2
,
1
)
l
o
g
(
e
x
0
,
1
+
x
1
,
2
+
t
1
,
2
+
e
x
0
,
2
+
x
1
,
2
+
t
2
,
2
)
l
o
g
(
e
x
0
,
1
+
x
1
,
2
+
t
1
,
2
+
e
x
0
,
2
+
x
1
,
2
+
t
2
,
2
)
)
+
(
x
2
,
1
x
2
,
2
x
2
,
1
x
2
,
2
)
+
(
t
1
,
1
t
1
,
2
t
2
,
1
t
2
,
2
)
=
(
l
o
g
(
e
x
0
,
1
+
x
1
,
1
+
t
1
,
1
+
e
x
0
,
2
+
x
1
,
1
+
t
2
,
1
)
+
x
2
,
1
+
t
1
,
1
l
o
g
(
e
x
0
,
1
+
x
1
,
1
+
t
1
,
1
+
e
x
0
,
2
+
x
1
,
1
+
t
2
,
1
)
+
x
2
,
2
+
t
1
,
2
l
o
g
(
e
x
0
,
1
+
x
1
,
2
+
t
1
,
2
+
e
x
0
,
2
+
x
1
,
2
+
t
2
,
2
)
+
x
2
,
1
+
t
2
,
1
l
o
g
(
e
x
0
,
1
+
x
1
,
2
+
t
1
,
2
+
e
x
0
,
2
+
x
1
,
2
+
t
2
,
2
)
+
x
2
,
2
+
t
2
,
2
)
scores = \begin{pmatrix} log(e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}}) & log(e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}}) \\ log(e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}}) & log(e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}}) \\ \end{pmatrix} + \begin{pmatrix} x_{2,1} & x_{2,2} \\ x_{2,1} & x_{2,2} \\ \end{pmatrix} + \begin{pmatrix} t_{1,1} & t_{1,2} \\ t_{2,1} & t_{2,2} \\ \end{pmatrix} = \begin{pmatrix} log(e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}}) + x_{2,1} + t_{1,1} & log(e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}}) + x_{2,2} + t_{1,2} \\ log(e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}}) + x_{2,1} + t_{2,1} & log(e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}}) + x_{2,2} + t_{2,2} \\ \end{pmatrix}
scores=(log(ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1)log(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2)log(ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1)log(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2))+(x2,1x2,1x2,2x2,2)+(t1,1t2,1t1,2t2,2)=(log(ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1)+x2,1+t1,1log(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2)+x2,1+t2,1log(ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1)+x2,2+t1,2log(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2)+x2,2+t2,2)
更新 p r e v i o u s = [ l o g ( e l o g ( e x 0 , 1 + x 1 , 1 + t 1 , 1 + e x 0 , 2 + x 1 , 1 + t 2 , 1 ) + x 2 , 1 + t 1 , 1 + e l o g ( e x 0 , 1 + x 1 , 2 + t 1 , 2 + e x 0 , 2 + x 1 , 2 + t 2 , 2 ) + x 2 , 1 + t 2 , 1 ) , l o g ( e l o g ( e x 0 , 1 + x 1 , 1 + t 1 , 1 + e x 0 , 2 + x 1 , 1 + t 2 , 1 ) + x 2 , 2 + t 1 , 2 + e l o g ( e x 0 , 1 + x 1 , 2 + t 1 , 2 + e x 0 , 2 + x 1 , 2 + t 2 , 2 ) + x 2 , 2 + t 2 , 2 ) ] = [ l o g ( ( e x 0 , 1 + x 1 , 1 + t 1 , 1 + e x 0 , 2 + x 1 , 1 + t 2 , 1 ) e x 2 , 1 + t 1 , 1 + ( e x 0 , 1 + x 1 , 2 + t 1 , 2 + e x 0 , 2 + x 1 , 2 + t 2 , 2 ) e x 2 , 1 + t 2 , 1 ) , l o g ( ( e x 0 , 1 + x 1 , 1 + t 1 , 1 + e x 0 , 2 + x 1 , 1 + t 2 , 1 ) e x 2 , 2 + t 1 , 2 + ( e x 0 , 1 + x 1 , 2 + t 1 , 2 + e x 0 , 2 + x 1 , 2 + t 2 , 2 ) e x 2 , 2 + t 2 , 2 ) ] \begin{aligned} previous &= [log(e^{log(e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}}) + x_{2,1} + t_{1,1}} + e^{log(e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}}) + x_{2,1} + t_{2,1}}), \\ & log(e^{log(e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}}) + x_{2,2} + t_{1,2}} + e^{log(e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}}) + x_{2,2} + t_{2,2}})] \\ & = [log((e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}})e^{x_{2,1} + t_{1,1}} + (e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}})e^{x_{2,1} + t_{2,1}}), \\ & log((e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}})e^{x_{2,2} + t_{1,2}} + (e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}})e^{x_{2,2} + t_{2,2}})] \\ \end{aligned} previous=[log(elog(ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1)+x2,1+t1,1+elog(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2)+x2,1+t2,1),log(elog(ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1)+x2,2+t1,2+elog(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2)+x2,2+t2,2)]=[log((ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1)ex2,1+t1,1+(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2)ex2,1+t2,1),log((ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1)ex2,2+t1,2+(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2)ex2,2+t2,2)]
计算总分数
T
o
t
a
l
S
c
o
r
e
(
w
0
→
w
1
→
w
2
)
=
l
o
g
(
e
p
r
e
v
i
o
u
s
[
0
]
+
e
p
r
e
v
i
o
u
s
[
1
]
)
=
l
o
g
(
e
l
o
g
(
l
o
g
(
(
e
x
0
,
1
+
x
1
,
1
+
t
1
,
1
+
e
x
0
,
2
+
x
1
,
1
+
t
2
,
1
)
e
x
2
,
1
+
t
1
,
1
+
(
e
x
0
,
1
+
x
1
,
2
+
t
1
,
2
+
e
x
0
,
2
+
x
1
,
2
+
t
2
,
2
)
e
x
2
,
1
+
t
2
,
1
)
)
+
e
l
o
g
(
l
o
g
(
(
e
x
0
,
1
+
x
1
,
1
+
t
1
,
1
+
e
x
0
,
2
+
x
1
,
1
+
t
2
,
1
)
e
x
2
,
2
+
t
1
,
2
+
(
e
x
0
,
1
+
x
1
,
2
+
t
1
,
2
+
e
x
0
,
2
+
x
1
,
2
+
t
2
,
2
)
e
x
2
,
2
+
t
2
,
2
)
)
)
=
l
o
g
(
e
x
0
,
1
+
x
1
,
1
+
t
1
,
1
+
x
2
,
1
+
t
1
,
1
+
e
x
0
,
2
+
x
1
,
1
+
t
2
,
1
+
x
2
,
1
+
t
1
,
1
+
e
x
0
,
1
+
x
1
,
2
+
t
1
,
2
+
x
2
,
1
+
t
2
,
1
+
e
x
0
,
2
+
x
1
,
2
+
t
2
,
2
+
x
2
,
1
+
t
2
,
1
+
e
x
0
,
1
+
x
1
,
1
+
t
1
,
1
+
x
2
,
2
+
t
1
,
2
+
e
x
0
,
2
+
x
1
,
1
+
t
2
,
1
+
x
2
,
2
+
t
1
,
2
+
e
x
0
,
1
+
x
1
,
2
+
t
1
,
2
+
x
2
,
2
+
t
2
,
2
+
e
x
0
,
2
+
x
1
,
2
+
t
2
,
2
+
x
2
,
2
+
t
2
,
2
)
\begin{aligned} TotalScore(w_0 \to w_1 \to w_2) &= log(e^{previous[0]} + e^{previous[1]}) \\ &= log(e^{log(log((e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}})e^{x_{2,1} + t_{1,1}} + (e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}})e^{x_{2,1} + t_{2,1}}))} \\ & + e^{log(log((e^{x_{0,1} + x_{1,1} + t_{1,1}} + e^{x_{0,2} + x_{1,1} + t_{2,1}})e^{x_{2,2} + t_{1,2}} + (e^{x_{0,1} + x_{1,2} + t_{1,2}} + e^{x_{0,2} + x_{1,2} + t_{2,2}})e^{x_{2,2} + t_{2,2}}))}) \\ &= log(e^{x_{0,1} + x_{1,1} + t_{1,1} + x_{2,1} + t_{1,1}} \\ &+ e^{x_{0,2} + x_{1,1} + t_{2,1} + x_{2,1} + t_{1,1}} \\ &+ e^{x_{0,1} + x_{1,2} + t_{1,2} + x_{2,1} + t_{2,1}} \\ &+ e^{x_{0,2} + x_{1,2} + t_{2,2} + x_{2,1} + t_{2,1}} \\ &+ e^{x_{0,1} + x_{1,1} + t_{1,1} + x_{2,2} + t_{1,2}} \\ &+ e^{x_{0,2} + x_{1,1} + t_{2,1} + x_{2,2} + t_{1,2}} \\ &+ e^{x_{0,1} + x_{1,2} + t_{1,2} + x_{2,2} + t_{2,2}} \\ &+ e^{x_{0,2} + x_{1,2} + t_{2,2} + x_{2,2} + t_{2,2}}) \\ \end{aligned}
TotalScore(w0→w1→w2)=log(eprevious[0]+eprevious[1])=log(elog(log((ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1)ex2,1+t1,1+(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2)ex2,1+t2,1))+elog(log((ex0,1+x1,1+t1,1+ex0,2+x1,1+t2,1)ex2,2+t1,2+(ex0,1+x1,2+t1,2+ex0,2+x1,2+t2,2)ex2,2+t2,2)))=log(ex0,1+x1,1+t1,1+x2,1+t1,1+ex0,2+x1,1+t2,1+x2,1+t1,1+ex0,1+x1,2+t1,2+x2,1+t2,1+ex0,2+x1,2+t2,2+x2,1+t2,1+ex0,1+x1,1+t1,1+x2,2+t1,2+ex0,2+x1,1+t2,1+x2,2+t1,2+ex0,1+x1,2+t1,2+x2,2+t2,2+ex0,2+x1,2+t2,2+x2,2+t2,2)
可以发现,计算总分数其实是穷举法,但是只是列出的表达式看上去是穷举(第二个词的时候TotalScore是由四个路径构成,第三个词的时候TotalScore则是由八个路径构成),但是实际上计算的时候,一直都是Obj,previous与transition scores这三个矩阵的加法,所以动规解决了很多计算量…
推理阶段-动态规划
也是上面的步骤
- 计算当前Obs(Emission scores)
- 计算scores
s c o r e s = ( p r e v i o u s [ 0 ] p r e v i o u s [ 0 ] p r e v i o u s [ 1 ] p r e v i o u s [ 1 ] ) + ( O b s [ 0 ] O b s [ 1 ] O b s [ 0 ] O b s [ 1 ] ) + ( t 11 t 12 t 21 t 22 ) scores = \begin{pmatrix} previous[0] & previous[0] \\ previous[1] & previous[1] \\ \end{pmatrix} + \begin{pmatrix} Obs[0] & Obs[1] \\ Obs[0] & Obs[1] \\ \end{pmatrix} + \begin{pmatrix} t_{11} & t_{12} \\ t_{21} & t_{22} \\ \end{pmatrix} scores=(previous[0]previous[1]previous[0]previous[1])+(Obs[0]Obs[0]Obs[1]Obs[1])+(t11t21t12t22) - 更新 p r e v i o u s , p r e v i o u s = [ m a x ( s c o r e s [ 0 , 0 ] , s c o r e s [ 1 , 0 ] ) , m a x ( s c o r e s [ 0 , 1 ] , s c o r e s [ 1 , 1 ] ) ] previous, previous = [max(scores[0, 0], scores[1, 0]),max(scores[0, 1], scores[1, 1])] previous,previous=[max(scores[0,0],scores[1,0]),max(scores[0,1],scores[1,1])], previous装的是到当前时刻,从前面过来,到当前时刻该标签的分数最大的那条路径
- 将分数保留在
α
0
\alpha_0
α0里,对应列索引保留在
α
1
\alpha_1
α1里(
α
1
\alpha_1
α1表示上一个节点是什么标签,关键是
t
t
t矩阵(transition scores)的下标,)
α 0 = [ ( 0.5 , 0.4 ) ] , α 1 = [ ( 1 , 1 ) ] \alpha_0 = [(0.5,0.4)], \alpha_1 = [(1,1)] α0=[(0.5,0.4)],α1=[(1,1)]
以三个单词为例,最终
α
0
\alpha_0
α0与
α
1
\alpha_1
α1中存储的值如下
α
0
=
[
(
0.5
,
0.4
)
,
(
0.8
,
0.9
)
]
,
α
1
=
[
(
1
,
1
)
,
(
1
,
0
)
]
\alpha_0 = [(0.5,0.4),(0.8,0.9)], \alpha_1 = [(1,1),(1,0)]
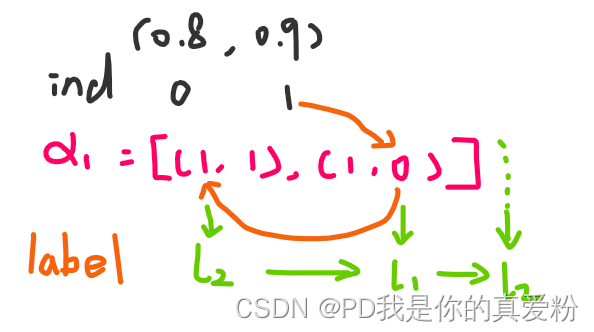
α0=[(0.5,0.4),(0.8,0.9)],α1=[(1,1),(1,0)]
我们选择最大的分数0.9,0.9本身是标签2,他的前一个节点是标签0,在前一个节点是标签1,所以就能得到路径,具体路径选择如下图所示